1 3 Divided By 4
elan
Sep 20, 2025 · 5 min read
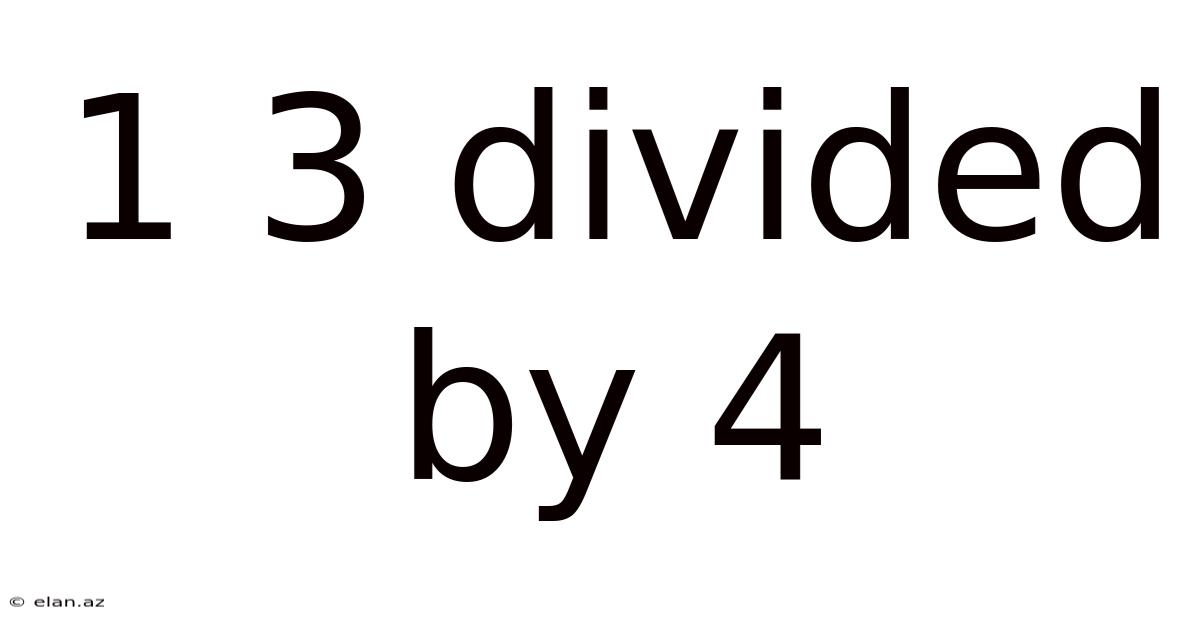
Table of Contents
Decoding 1 3/4: A Deep Dive into Mixed Numbers and Their Applications
Understanding fractions, especially mixed numbers like 1 3/4, is fundamental to grasping many aspects of mathematics and its real-world applications. This seemingly simple number holds a wealth of mathematical concepts, from basic arithmetic to more advanced algebraic manipulations. This article will explore 1 3/4 in detail, examining its structure, different representations, practical uses, and the underlying principles that govern its behavior within mathematical operations. We'll delve into the conversion between mixed numbers and improper fractions, explore its decimal equivalent, and even touch upon its significance in various fields.
Understanding Mixed Numbers
A mixed number combines a whole number and a proper fraction. In 1 3/4, the '1' represents one whole unit, and the '3/4' represents three-quarters of another unit. This representation is particularly intuitive and useful for visualizing quantities. Imagine you have one whole pizza and three-quarters of another; that's exactly what 1 3/4 represents.
Converting to an Improper Fraction
While the mixed number form (1 3/4) is easily understood visually, many mathematical operations are simpler when working with improper fractions. An improper fraction has a numerator that is greater than or equal to its denominator. To convert 1 3/4 to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 1 * 4 = 4
- Add the numerator: 4 + 3 = 7
- Keep the same denominator: The denominator remains 4.
Therefore, 1 3/4 is equivalent to the improper fraction 7/4.
Converting to a Decimal
Converting fractions to decimals is another essential skill. To convert 7/4 (or 1 3/4) to a decimal, we simply perform the division: 7 ÷ 4 = 1.75. This decimal representation is frequently used in calculations involving money, measurements, and other real-world applications.
Mathematical Operations with 1 3/4
Let's explore how 1 3/4 behaves in various mathematical operations. It's often easier to perform these operations using the improper fraction form (7/4).
-
Addition: Adding 1 3/4 to another mixed number, say 2 1/2, is best done by converting both to improper fractions: 7/4 + 5/2. Find a common denominator (4), so we have 7/4 + 10/4 = 17/4. This can be converted back to a mixed number: 4 1/4.
-
Subtraction: Similarly, subtracting 1 3/4 from 3 would be: 3 - 7/4. Convert 3 to the improper fraction 12/4, then subtract: 12/4 - 7/4 = 5/4 or 1 1/4.
-
Multiplication: Multiplying 1 3/4 by another number, say 2, is simpler as an improper fraction: (7/4) * 2 = 14/4 = 7/2 = 3 1/2.
-
Division: Dividing by 1 3/4 is done by inverting the fraction and multiplying. For example, 4 divided by 1 3/4 becomes 4 ÷ (7/4) = 4 * (4/7) = 16/7 = 2 2/7.
Real-World Applications of 1 3/4
The number 1 3/4 pops up surprisingly often in everyday life:
-
Cooking and Baking: Many recipes use measurements in fractions. A recipe might call for 1 3/4 cups of flour or 1 3/4 teaspoons of baking powder.
-
Measurement and Construction: Construction projects often involve measurements that are not whole numbers. A piece of lumber might be 1 3/4 feet long, or a wall might be 1 3/4 inches thick.
-
Finance: While money is usually expressed in decimals, understanding fractions helps in calculating percentages, discounts, or interest rates. For instance, figuring out 1 3/4% interest on a loan requires converting it to a decimal (0.0175).
-
Data Analysis: In data analysis and statistics, you may encounter data points represented as mixed numbers, requiring conversion to decimals or improper fractions for further calculations.
Further Exploration: Advanced Concepts
While we have covered the basics, let's delve into slightly more advanced concepts related to 1 3/4:
-
Approximation: In situations where exact precision isn't needed, 1 3/4 can be approximated to 2. This simplification is useful for quick estimations or mental calculations.
-
Algebra: 1 3/4 (or its equivalent 7/4) can be used in algebraic expressions and equations. Solving for 'x' in an equation like x + 7/4 = 5 involves basic algebraic manipulations.
-
Geometry: Understanding fractions is crucial in geometry, particularly in calculating areas and volumes involving fractional dimensions.
-
Calculus: The concept of limits in calculus builds upon the fundamental understanding of fractions and their behavior as values approach zero or infinity.
Frequently Asked Questions (FAQs)
-
What is 1 3/4 as a percentage? To express 1 3/4 as a percentage, convert it to a decimal (1.75) and then multiply by 100: 1.75 * 100 = 175%.
-
Can 1 3/4 be simplified further? No, 1 3/4 is already in its simplest form. The fraction 3/4 cannot be reduced because 3 and 4 share no common factors other than 1.
-
How do I add 1 3/4 and 2/3? Convert both to improper fractions with a common denominator (12): 7/4 becomes 21/12, and 2/3 becomes 8/12. Add them: 21/12 + 8/12 = 29/12 which simplifies to 2 5/12.
-
What is the reciprocal of 1 3/4? The reciprocal is found by inverting the improper fraction: 7/4 becomes 4/7.
Conclusion
Understanding the seemingly simple number 1 3/4 reveals a surprising depth of mathematical concepts. From basic arithmetic to advanced applications, mastering the manipulation of mixed numbers and their conversion to improper fractions and decimals is crucial. The ability to work comfortably with such numbers extends far beyond the classroom, proving essential in various real-world scenarios, from cooking and construction to finance and data analysis. By grasping the fundamental principles outlined in this article, you can confidently tackle various mathematical challenges involving fractions and strengthen your overall mathematical proficiency. Remember that consistent practice and a willingness to explore different approaches are key to mastering these fundamental concepts. The journey of understanding mathematics is a continuous one, and each step, no matter how small, contributes significantly to building a strong foundation.
Latest Posts
Latest Posts
-
Cross Section Of A Prism
Sep 20, 2025
-
How Big Is 13 Inches
Sep 20, 2025
-
Is English Difficult To Learn
Sep 20, 2025
-
Addition And Subtraction Year 2
Sep 20, 2025
-
Image Of An Animal Cell
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.