1 3 Divided By 8
elan
Sep 23, 2025 · 6 min read
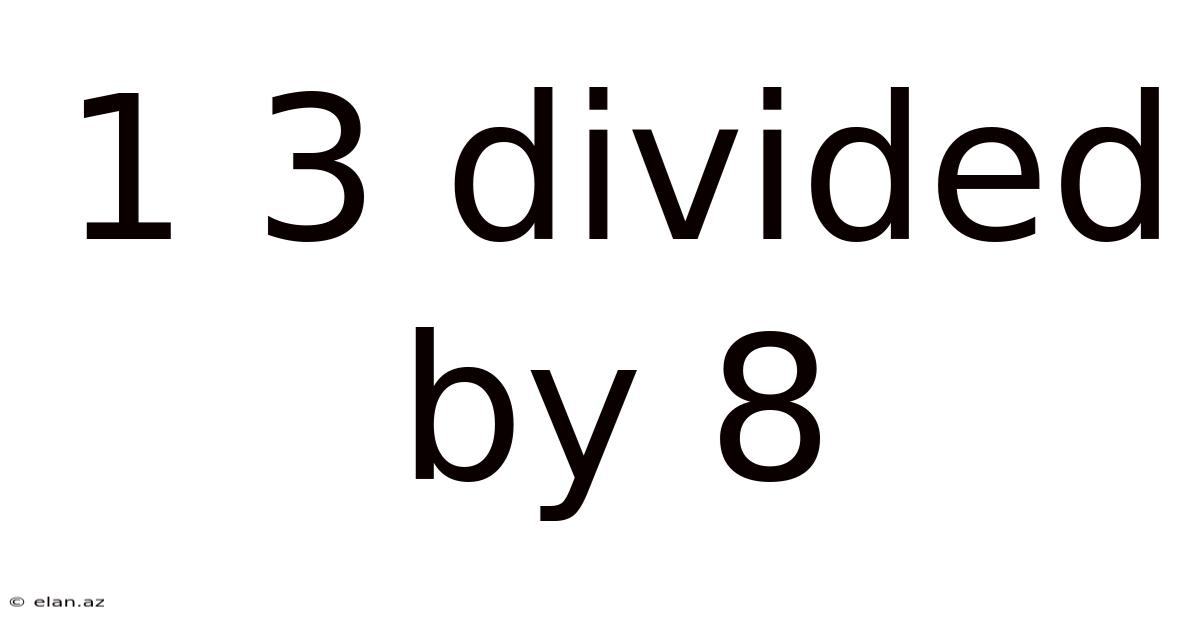
Table of Contents
Unpacking 1 3/8: A Deep Dive into Fractions and Their Applications
This article explores the seemingly simple calculation of 1 3/8, delving far beyond the basic arithmetic to reveal the underlying principles of fractions, their practical applications, and their importance in various fields. We'll uncover the different ways to interpret and manipulate this mixed number, demonstrating its significance in everyday life and advanced mathematics. Understanding 1 3/8 isn't just about finding the answer; it's about grasping the fundamental concepts that govern a significant portion of mathematics.
Understanding the Components: Mixed Numbers and Improper Fractions
Before we tackle 1 3/8, let's clarify the terminology. 1 3/8 is a mixed number. A mixed number combines a whole number (1 in this case) and a proper fraction (3/8). A proper fraction has a numerator (the top number, 3) smaller than the denominator (the bottom number, 8).
We can also represent 1 3/8 as an improper fraction. An improper fraction has a numerator greater than or equal to its denominator. To convert 1 3/8 to an improper fraction, we multiply the whole number (1) by the denominator (8), add the numerator (3), and keep the same denominator:
(1 * 8) + 3 = 11
Therefore, 1 3/8 is equivalent to 11/8. Both representations are valid and useful depending on the context.
Calculating 1 3/8 in Different Contexts
The simple act of "calculating" 1 3/8 depends on the operation involved. If the instruction is simply to represent it in a different form (as shown above), that's one type of calculation. However, if it's part of a larger equation, the approach will change. Let's explore different scenarios:
1. Simplifying the Fraction
In its current forms (1 3/8 or 11/8), the fraction is already in its simplest form. The numerator (11) and denominator (8) share no common factors other than 1. Simplification involves dividing both the numerator and denominator by their greatest common divisor (GCD). Since the GCD of 11 and 8 is 1, further simplification is not possible.
2. Converting to a Decimal
Converting a fraction to a decimal is a common task. To convert 11/8 to a decimal, we perform the division:
11 ÷ 8 = 1.375
Therefore, 1 3/8 is equal to 1.375. This decimal representation is particularly useful when working with calculators or computers, or when comparing fractions to decimal numbers.
3. Using 1 3/8 in Addition, Subtraction, Multiplication, and Division
The way we handle 1 3/8 changes dramatically depending on the operation.
- Addition/Subtraction: When adding or subtracting fractions, it's crucial to have a common denominator. If we're adding 1 3/8 to another fraction, we'll first convert it to an improper fraction (11/8) and then find a common denominator with the other fraction. For example:
1 3/8 + 1/2 = 11/8 + 4/8 = 15/8 = 1 7/8
- Multiplication: Multiplying fractions is relatively straightforward. We can multiply 1 3/8 by another fraction either in its mixed number form or improper fraction form. For instance, multiplying 1 3/8 by 2:
1 3/8 * 2 = 11/8 * 2 = 22/8 = 2 6/8 = 2 3/4
- Division: Dividing fractions involves inverting the second fraction and then multiplying. For example, dividing 1 3/8 by 1/4:
1 3/8 ÷ 1/4 = 11/8 ÷ 1/4 = 11/8 * 4/1 = 44/8 = 5 4/8 = 5 1/2
The Practical Applications of Understanding 1 3/8 and Fractions in General
The seemingly simple fraction 1 3/8 finds applications in numerous fields, showcasing the fundamental importance of fractional understanding:
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Fractions are used extensively in blueprints, material calculations, and ensuring structural integrity. A carpenter might need 1 3/8 inches of wood for a specific joinery.
-
Cooking and Baking: Recipes often call for fractional measurements of ingredients, ensuring consistent results. A baker might require 1 3/8 cups of flour for a particular bread recipe.
-
Finance: Fractions are used to represent portions of ownership (shares of stock) or interest rates. Understanding fractions is critical for making informed financial decisions.
-
Data Analysis and Statistics: Fractions and decimals are fundamental to data analysis and statistics. Representing proportions, calculating averages, and interpreting statistical results all rely on fractional understanding.
-
Science: Fractions are ubiquitous in scientific measurements and calculations. They are essential for understanding ratios, proportions, and representing experimental data.
-
Computer Science: While computers use binary systems, understanding fractions is crucial for programmers working with data representation, image manipulation, and game development.
Delving Deeper: Exploring Related Mathematical Concepts
Understanding 1 3/8 opens doors to more advanced mathematical concepts:
-
Ratio and Proportion: Fractions represent ratios, showing the relationship between two quantities. For example, 1 3/8 could represent a ratio of 11 parts to 8 parts. Understanding ratios is critical for solving proportion problems.
-
Percentage: Percentages are simply fractions expressed as parts of 100. We can convert 1 3/8 to a percentage by converting it to a decimal (1.375) and multiplying by 100: 137.5%.
-
Algebra: Fractions are integral to algebraic expressions and equations. Solving for variables often involves manipulating fractions.
-
Calculus: Calculus builds upon foundational mathematical concepts, including fractions, to deal with rates of change and areas under curves.
Frequently Asked Questions (FAQ)
-
What is the simplest form of 1 3/8? The simplest form is already 1 3/8 or its equivalent improper fraction, 11/8.
-
How do I convert 1 3/8 to a decimal? Divide the numerator (11) by the denominator (8): 11 ÷ 8 = 1.375
-
Can 1 3/8 be expressed as a percentage? Yes, 137.5%
-
What is the reciprocal of 1 3/8? The reciprocal is found by inverting the fraction. The reciprocal of 11/8 is 8/11.
-
Why are fractions important? Fractions are fundamental to many aspects of mathematics and science and essential for accurately representing parts of wholes. They are crucial for numerous practical applications in daily life and various professions.
Conclusion
While the calculation of 1 3/8 might appear trivial at first glance, this exploration reveals the rich mathematical landscape underlying this seemingly simple number. Understanding fractions, in their various forms (mixed numbers, improper fractions, decimals, percentages), is essential for navigating the world around us, whether it's measuring ingredients for a recipe, understanding financial reports, or tackling complex scientific problems. This deep dive into 1 3/8 illustrates not only the versatility of this specific fraction but also the broader importance of grasping fractional concepts within the larger context of mathematics and its numerous practical applications. The seemingly simple task of understanding 1 3/8 unlocks a world of mathematical possibilities.
Latest Posts
Latest Posts
-
Cscs Blue Card Mock Test
Sep 23, 2025
-
Social Enterprise Advantages And Disadvantages
Sep 23, 2025
-
X X 1 X 2
Sep 23, 2025
-
I Can Smell Your Nappy
Sep 23, 2025
-
Calculator For Coefficient Of Variation
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.