1 4 Divided By 3
elan
Sep 18, 2025 · 5 min read
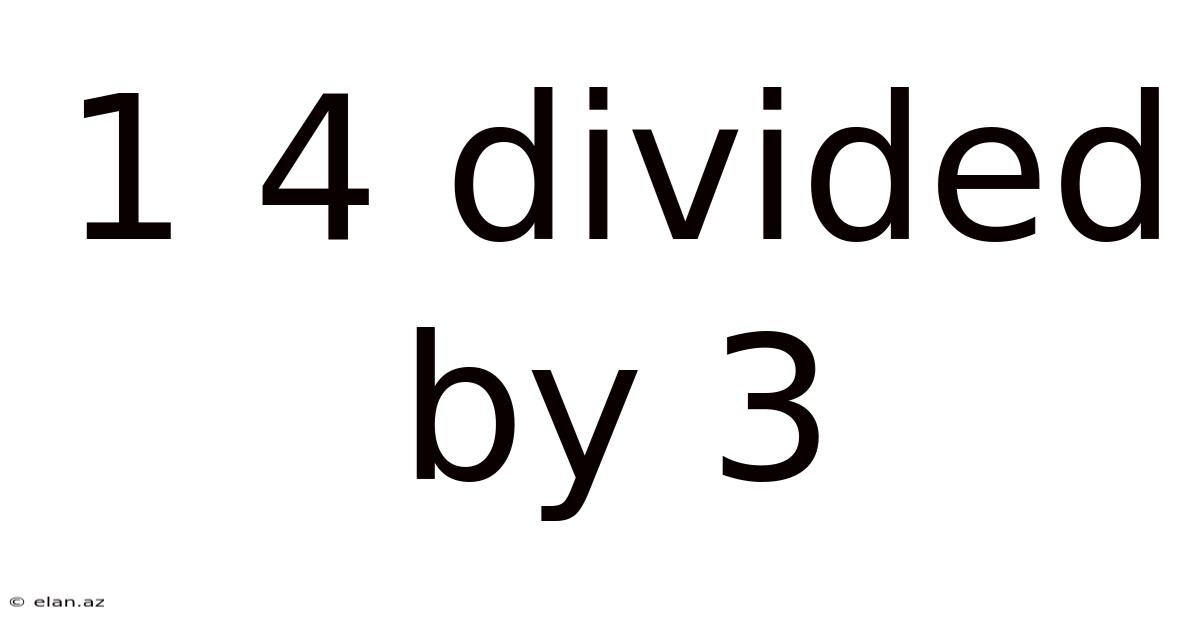
Table of Contents
Unpacking 1/4 Divided by 3: A Deep Dive into Fraction Division
Understanding fraction division can feel like navigating a mathematical maze, especially when dealing with seemingly simple problems like 1/4 divided by 3. This article will demystify this process, providing a comprehensive explanation that goes beyond a simple answer, exploring the underlying principles and offering multiple approaches to solve this problem and similar ones. We'll cover the conceptual understanding, various methods for solving the problem, practical applications, and frequently asked questions to ensure a complete and thorough grasp of the topic.
Understanding the Problem: 1/4 ÷ 3
At its core, the problem "1/4 divided by 3" asks: "If we divide one-quarter into three equal parts, what is the size of each part?" This highlights the crucial concept that division is about splitting something into a specified number of equal portions. We're not just manipulating numbers; we're dealing with proportional parts of a whole.
Method 1: The "Keep, Change, Flip" Method
This popular method provides a straightforward algorithm for dividing fractions. The steps are:
- Keep the first fraction the same: 1/4
- Change the division sign (÷) to a multiplication sign (×)
- Flip (find the reciprocal of) the second fraction. Since 3 can be written as 3/1, its reciprocal is 1/3.
So, the problem becomes: 1/4 × 1/3
Multiplying fractions involves multiplying the numerators together and the denominators together:
(1 × 1) / (4 × 3) = 1/12
Therefore, 1/4 divided by 3 equals 1/12.
Method 2: Visual Representation
Visualizing the problem can be incredibly helpful, especially for beginners. Imagine a pizza cut into four equal slices. You have one slice (1/4 of the pizza). Now, you need to divide that single slice into three equal parts. Each of these smaller parts represents 1/12 of the whole pizza.
Method 3: Understanding Division as Repeated Subtraction
While less efficient for this particular problem, understanding division as repeated subtraction provides valuable insight. How many times can you subtract 3 from 1/4? This approach is less intuitive with fractions, but it reinforces the fundamental concept of division. This method is better suited for whole numbers or when dealing with larger fractions. Instead, consider how many times 3 fits into 1/4, leading to the same solution of 1/12.
Method 4: Converting to Decimals
Another approach involves converting the fraction to its decimal equivalent before dividing.
1/4 = 0.25
Now, divide 0.25 by 3:
0.25 ÷ 3 ≈ 0.08333...
This decimal, 0.08333..., is the decimal representation of 1/12. While this method yields the correct answer, it's generally less precise and can lead to rounding errors, especially when dealing with repeating decimals.
The Importance of Understanding the Reciprocal
The "keep, change, flip" method relies heavily on the concept of the reciprocal. The reciprocal of a number is simply 1 divided by that number. For example:
- The reciprocal of 2 is 1/2
- The reciprocal of 5/7 is 7/5
- The reciprocal of 1 is 1
Understanding reciprocals is fundamental to mastering fraction division. When dividing by a fraction, we are essentially multiplying by its reciprocal. This is because division is the inverse operation of multiplication.
Practical Applications: Real-World Examples
Understanding fraction division isn't just an academic exercise; it has numerous real-world applications. Consider these examples:
- Baking: A recipe calls for 1/4 cup of sugar, but you want to make only 1/3 of the recipe. How much sugar do you need? (1/4 ÷ 3 = 1/12 cup)
- Construction: You need to cut a piece of wood that's 1/4 of a meter long into three equal pieces. How long is each piece? (1/4 ÷ 3 = 1/12 meter)
- Sharing Resources: You have 1/4 of a pizza and want to share it equally among three friends. How much pizza does each person get? (1/4 ÷ 3 = 1/12 of the pizza)
Expanding the Concept: Dividing Fractions by Fractions
The principles discussed above extend to problems involving dividing fractions by other fractions. For instance, consider the problem 2/5 ÷ 3/4. Using the "keep, change, flip" method:
- Keep: 2/5
- Change: ÷ becomes ×
- Flip: 3/4 becomes 4/3
The problem becomes: (2/5) × (4/3) = 8/15
Frequently Asked Questions (FAQ)
Q: Why does the "keep, change, flip" method work?
A: The method is a shortcut derived from the properties of multiplication and reciprocals. Dividing by a fraction is equivalent to multiplying by its reciprocal. This is because multiplying by a reciprocal "undoes" the division.
Q: Can I divide fractions using a calculator?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for problem-solving and avoiding reliance solely on technology.
Q: What if I have a mixed number (e.g., 1 1/4) involved in the division?
A: First, convert the mixed number into an improper fraction. For example, 1 1/4 becomes 5/4. Then, apply the "keep, change, flip" method or any other method you're comfortable with.
Q: Is there a difference between dividing a fraction by a whole number and dividing a whole number by a fraction?
A: Yes, there's a conceptual difference. Dividing a fraction by a whole number means splitting the fraction into smaller pieces. Dividing a whole number by a fraction means determining how many times the fraction fits into the whole number. The "keep, change, flip" method works for both scenarios, but the interpretation of the result differs.
Conclusion: Mastering Fraction Division
Mastering fraction division is a cornerstone of mathematical understanding. While the "keep, change, flip" method offers a streamlined approach, a deeper understanding of the underlying principles—including the concept of reciprocals and the different interpretations of division—is essential for applying these skills effectively in various contexts. By practicing different methods and visualizing the problems, you can build confidence and proficiency in tackling even more complex fraction division problems. Remember that mathematics is a journey of understanding, not just memorization; embrace the process and enjoy the challenge!
Latest Posts
Latest Posts
-
What Is Income From Operations
Sep 18, 2025
-
One Fifth In Decimal Form
Sep 18, 2025
-
Words Ending With A Y
Sep 18, 2025
-
Meaning Of Bought In Hindi
Sep 18, 2025
-
Put Into Use 8 Letters
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.