10 11 As A Decimal
elan
Sep 22, 2025 · 6 min read
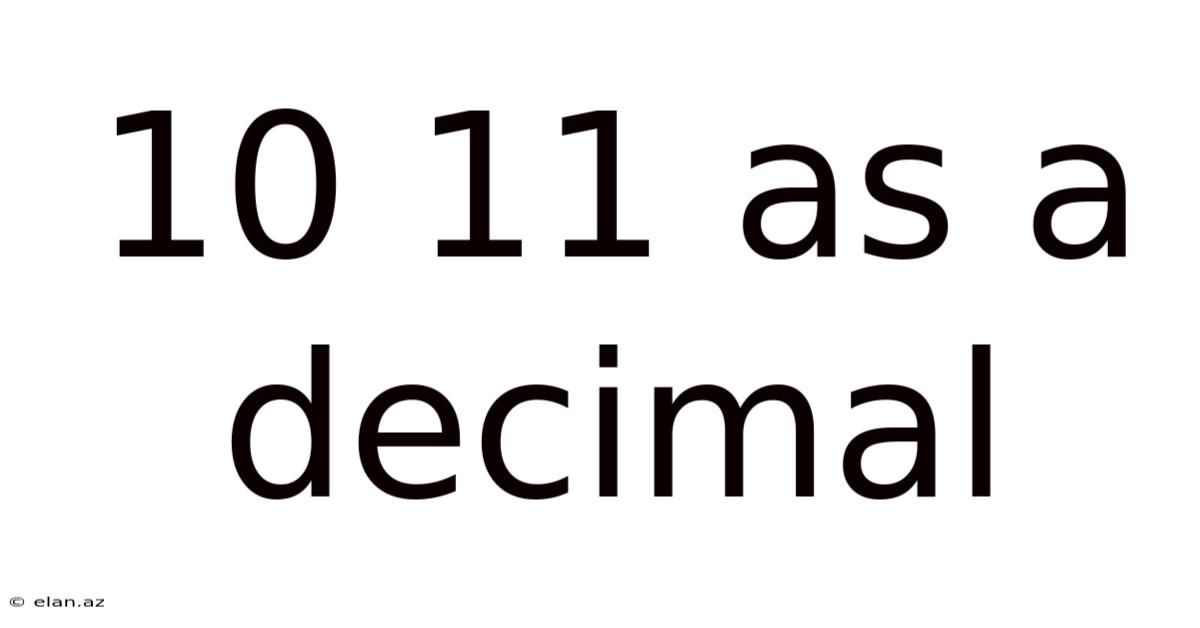
Table of Contents
Understanding 10/11 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide delves into the process of converting the fraction 10/11 into its decimal equivalent, exploring different methods, providing detailed explanations, and addressing frequently asked questions. Understanding this seemingly simple conversion unlocks a deeper appreciation of decimal representation and its relationship to fractions. We'll cover not only the how but also the why, ensuring a thorough and engaging learning experience.
Understanding Fractions and Decimals
Before diving into the conversion of 10/11, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 10/11, 10 is the numerator and 11 is the denominator. This means we have 10 parts out of a total of 11 equal parts.
A decimal, on the other hand, represents a number based on the power of 10. It uses a decimal point to separate the whole number part from the fractional part. For example, 0.5 represents one-half (1/2), and 0.75 represents three-quarters (3/4). Decimals are often preferred in practical applications because they are easier to manipulate in calculations and comparisons.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. In this method, we divide the numerator (10) by the denominator (11).
-
Set up the long division: Write 10 as the dividend (inside the division symbol) and 11 as the divisor (outside the division symbol). Add a decimal point followed by zeros to the dividend to facilitate the division process. This allows us to continue the division even if the division doesn't result in a whole number.
-
Perform the division: Begin by dividing 11 into 10. Since 11 is larger than 10, the result of this division is 0. Place the 0 above the 10.
-
Bring down the next digit: Since there is no remainder after dividing 10 by 11, add a zero to the dividend.
-
Continue the division: Now we have 100 as the new dividend. 11 goes into 100 nine times (9 x 11 = 99). Place the 9 above the zero you just brought down.
-
Subtract and bring down: Subtract 99 from 100, leaving a remainder of 1. Bring down another zero.
-
Repeat the process: Now we have 10 as the new dividend. The process repeats, and we find that the quotient is 0.909090...
-
Identify the repeating pattern: Notice that the digits 9 and 0 repeat indefinitely. This indicates that the decimal representation of 10/11 is a repeating decimal.
Therefore, 10/11 as a decimal is 0.90909090… This is often written as 0.$\overline{90}$, where the bar above 90 indicates the repeating sequence.
Method 2: Using a Calculator
Modern calculators provide a quick and efficient way to convert fractions to decimals. Simply enter the fraction 10/11 into the calculator and press the "equals" button. The calculator will directly display the decimal equivalent, which, in this case, will be 0.90909090... (or a similar representation showing the repeating nature of the decimal). While convenient, understanding the underlying principles of long division is crucial for grasping the mathematical concept.
The Significance of Repeating Decimals
The result of converting 10/11 to a decimal reveals a repeating decimal. This is common when the denominator of the fraction cannot be expressed as a product of only 2s and 5s (the prime factors of 10). Since the denominator, 11, is a prime number other than 2 or 5, the resulting decimal will be a repeating decimal. This highlights a key relationship between rational numbers (numbers expressible as fractions) and their decimal representations. Rational numbers can be represented either as terminating decimals (like 0.25 for 1/4) or as repeating decimals (like 0.$\overline{90}$ for 10/11).
Approximations and Rounding
In practical applications, it might be necessary to use an approximation of the decimal value instead of the infinitely repeating decimal. We can round the decimal to a specific number of decimal places. For example:
- Rounded to one decimal place: 0.9
- Rounded to two decimal places: 0.91
- Rounded to three decimal places: 0.909
The level of accuracy required dictates the number of decimal places to use. Remember that rounding introduces a small error, but often this is acceptable for many purposes.
Practical Applications of Decimal Conversions
Converting fractions to decimals is crucial in numerous applications:
-
Financial calculations: Calculating interest rates, discounts, and proportions often involve decimal representation.
-
Scientific measurements: Measurements in science and engineering frequently use decimal notation for precision.
-
Everyday calculations: Dividing quantities, sharing resources, or calculating percentages often necessitates fraction-to-decimal conversion.
-
Computer programming: Decimal representation is essential in computer programming for handling numerical data and performing calculations.
-
Data analysis and statistics: Decimal numbers are widely used in statistical analysis and data representation.
Frequently Asked Questions (FAQ)
Q1: Why is 10/11 a repeating decimal?
A1: A fraction results in a repeating decimal when its denominator (in its simplest form) contains prime factors other than 2 and 5. Since 11 is a prime number other than 2 or 5, the resulting decimal representation is a repeating decimal.
Q2: How accurate is rounding a repeating decimal?
A2: Rounding introduces a small error. The accuracy depends on the number of decimal places retained. The more decimal places retained, the smaller the error. However, the error will never be completely eliminated unless the entire repeating sequence is included, which is impossible for infinitely repeating decimals.
Q3: Are there other methods to convert fractions to decimals?
A3: While long division and calculators are the most common methods, other techniques exist, such as converting the fraction to an equivalent fraction with a denominator that is a power of 10. However, this method is not always feasible, especially for fractions with denominators that are not easily converted to powers of 10.
Q4: What if the fraction is an improper fraction (numerator is larger than denominator)?
A4: An improper fraction can be converted to a mixed number (a whole number and a proper fraction) before converting to a decimal. The whole number part remains unchanged, and the proper fraction part is converted to a decimal using the methods described above. For example, 12/11 = 1 + 1/11, and 1/11 can be converted to a decimal using long division.
Q5: Can all fractions be expressed as decimals?
A5: Yes, all fractions can be expressed as decimals. They will either be terminating decimals or repeating decimals.
Conclusion
Converting the fraction 10/11 to its decimal equivalent, 0.$\overline{90}$, illustrates a fundamental concept in mathematics: the relationship between fractions and decimals. Understanding the method of long division and recognizing the characteristics of repeating decimals are crucial skills for various mathematical applications. This detailed guide not only provides the answer but also equips you with the knowledge and understanding to tackle similar conversions confidently. Remember, the process is not just about finding the answer; it's about building a strong foundation in mathematical principles.
Latest Posts
Latest Posts
-
Oil Heater B And Q
Sep 22, 2025
-
Us Dollar To Senegal Cfa
Sep 22, 2025
-
170 Cm To Feet Inch
Sep 22, 2025
-
Cubic Metres To Cubic Feet
Sep 22, 2025
-
Sample Statement Of Account Template
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 10 11 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.