10 12 As A Percent
elan
Sep 24, 2025 · 5 min read
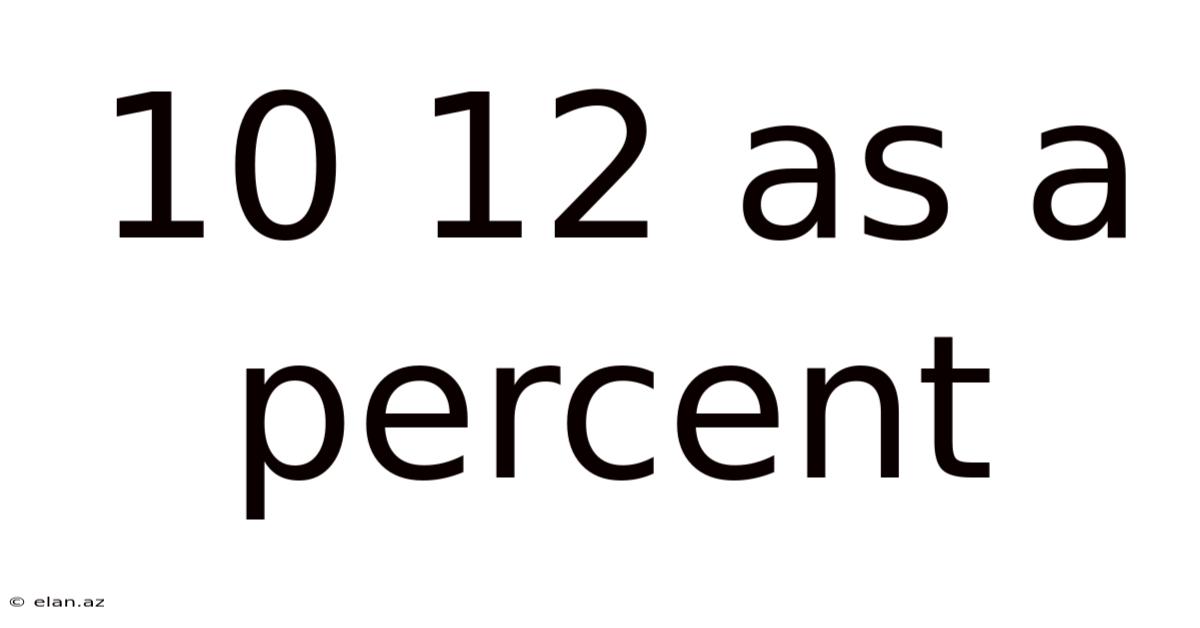
Table of Contents
Understanding 10/12 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This article delves deep into the process of converting the fraction 10/12 into a percentage, explaining the method step-by-step and exploring related concepts. We'll also address common misconceptions and provide additional examples to solidify your understanding. This guide aims to equip you with not just the answer, but a thorough grasp of the underlying principles.
Understanding Fractions and Percentages
Before we tackle 10/12, let's review the basics. A fraction represents a part of a whole. The top number is the numerator, indicating the number of parts we have, and the bottom number is the denominator, indicating the total number of parts in the whole. A percentage, on the other hand, represents a fraction out of 100. The symbol % signifies "per hundred."
Converting 10/12 to a Percentage: A Step-by-Step Guide
There are two main ways to convert a fraction like 10/12 to a percentage:
Method 1: Simplifying the Fraction and then Converting
This method involves simplifying the fraction to its lowest terms before converting it to a percentage. This often makes the calculations easier.
-
Simplify the fraction: Both 10 and 12 are divisible by 2. Therefore, we can simplify 10/12 by dividing both the numerator and the denominator by 2:
10 ÷ 2 / 12 ÷ 2 = 5/6
-
Convert the simplified fraction to a decimal: To convert a fraction to a decimal, divide the numerator by the denominator:
5 ÷ 6 ≈ 0.8333... (the 3s repeat infinitely)
-
Convert the decimal to a percentage: To convert a decimal to a percentage, multiply by 100 and add the % symbol:
0.8333... × 100 ≈ 83.33%
Therefore, 10/12 simplifies to approximately 83.33%. The "..." indicates that the decimal is recurring, meaning the 3s continue indefinitely. For practical purposes, rounding to two decimal places is usually sufficient.
Method 2: Direct Conversion to Percentage
This method involves directly converting the fraction to a percentage without simplifying first.
-
Convert the fraction to a decimal: Divide the numerator by the denominator:
10 ÷ 12 ≈ 0.8333...
-
Convert the decimal to a percentage: Multiply by 100 and add the % symbol:
0.8333... × 100 ≈ 83.33%
As you can see, both methods yield the same result. The first method, involving simplification, is often preferred as it can simplify subsequent calculations, particularly with larger fractions.
Understanding the Recurring Decimal
The recurring decimal 0.8333... is an important aspect of this conversion. It highlights that some fractions cannot be expressed exactly as a finite decimal. The recurring 3 signifies that the decimal continues infinitely. In practical applications, rounding to a suitable number of decimal places is necessary. For instance, you might round 83.333...% to 83.3% or even 83% depending on the required level of precision.
Real-World Applications of Percentage Conversions
Converting fractions to percentages is crucial in many real-world scenarios:
- Sales and discounts: If a store offers a discount of 10/12 (or 5/6) on an item, this translates to an 83.33% discount.
- Financial analysis: Percentage changes in stock prices, interest rates, and other financial metrics are frequently calculated using fraction-to-percentage conversions.
- Surveys and statistics: Data from surveys and polls is often presented as percentages, requiring the conversion of raw data (often in fractions) to percentage representation.
- Academic performance: Grades and test scores are often expressed as percentages, making understanding fraction-to-percentage conversions essential for evaluating academic performance.
- Scientific measurements and experiments: In many scientific applications, measurements and data are represented as fractions and percentages.
Further Examples
Let's apply the same method to other fractions to solidify your understanding:
-
Converting 1/4 to a percentage:
- Convert to decimal: 1 ÷ 4 = 0.25
- Convert to percentage: 0.25 × 100 = 25%
-
Converting 3/5 to a percentage:
- Convert to decimal: 3 ÷ 5 = 0.6
- Convert to percentage: 0.6 × 100 = 60%
-
Converting 7/8 to a percentage:
- Convert to decimal: 7 ÷ 8 = 0.875
- Convert to percentage: 0.875 × 100 = 87.5%
Frequently Asked Questions (FAQ)
-
Q: Why is it important to simplify fractions before converting to a percentage?
A: Simplifying makes the division process easier and reduces the chances of errors, particularly with larger fractions. It also results in a cleaner and more manageable decimal representation.
-
Q: What if I get a recurring decimal when converting a fraction to a percentage?
A: Recurring decimals are common when converting fractions to percentages. You should round the decimal to a reasonable number of decimal places based on the context of the problem.
-
Q: Can I convert a mixed number (e.g., 1 1/2) to a percentage?
A: Yes, first convert the mixed number to an improper fraction (in this case, 3/2), and then follow the steps outlined above to convert it to a percentage. 3/2 converts to 1.5, which equals 150%.
Conclusion
Converting 10/12 to a percentage, which results in approximately 83.33%, is a straightforward process that involves understanding the relationship between fractions, decimals, and percentages. By following the steps outlined above and practicing with different examples, you can build a strong understanding of this fundamental mathematical concept and apply it to a variety of real-world situations. Remember that the key is to first understand the underlying principles of fractions and percentages, and then practice the conversion process until it becomes second nature. The ability to confidently handle percentage calculations will prove incredibly valuable in various aspects of your life, both academic and professional.
Latest Posts
Latest Posts
-
Difference Between Profit And Revenue
Sep 24, 2025
-
Quota Sampling Advantages And Disadvantages
Sep 24, 2025
-
1 3 4 In Millimeters
Sep 24, 2025
-
National Game Of Sri Lanka
Sep 24, 2025
-
How To Sketch A Bottle
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 10 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.