11 20 As A Percent
elan
Sep 23, 2025 · 5 min read
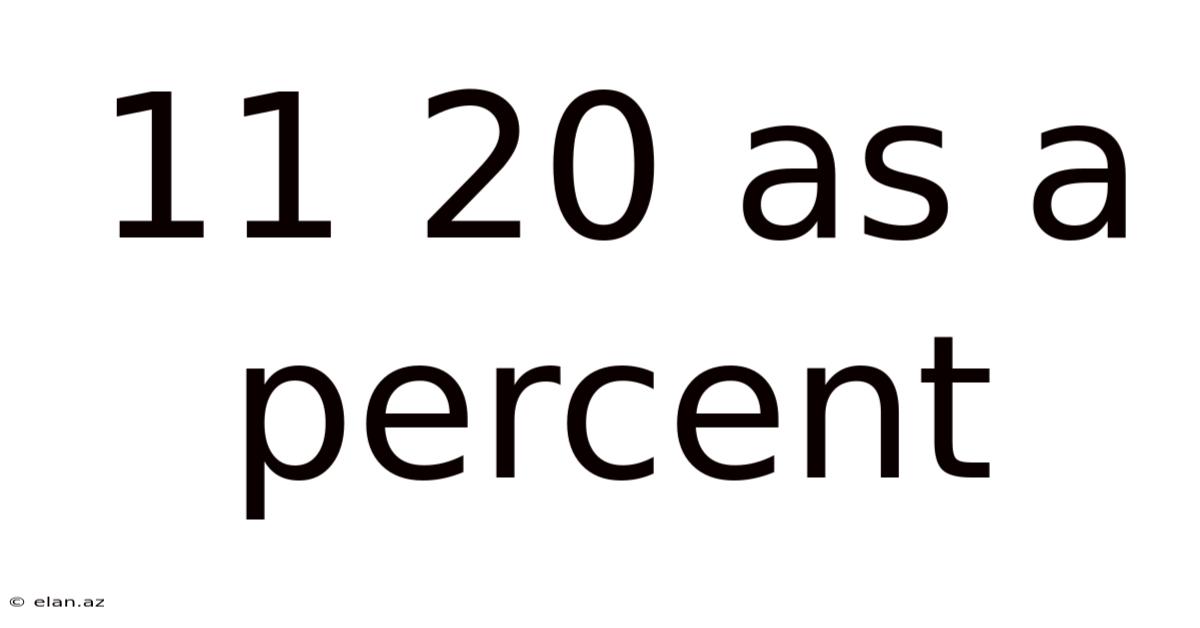
Table of Contents
11/20 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and sales tax to understanding statistics and interpreting data. This article provides a comprehensive guide on converting the fraction 11/20 into a percentage, explaining the process step-by-step, exploring the underlying mathematical principles, and offering practical examples. We'll also delve into related concepts and answer frequently asked questions to ensure a complete understanding.
Understanding Fractions and Percentages
Before diving into the conversion of 11/20, let's establish a solid foundation. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts out of 100 constitute a particular portion of the whole. Essentially, a percentage expresses a fraction with a denominator of 100.
Converting 11/20 to a Percentage: The Method
Converting a fraction to a percentage involves two key steps:
-
Convert the fraction to a decimal: This is done by dividing the numerator by the denominator. In our case, we divide 11 by 20:
11 ÷ 20 = 0.55
-
Convert the decimal to a percentage: This is done by multiplying the decimal by 100 and adding the percentage symbol (%).
0.55 × 100 = 55%
Therefore, 11/20 as a percentage is 55%.
A Deeper Dive into the Mathematics
The conversion from fraction to percentage fundamentally relies on the concept of equivalent fractions. We aim to find a fraction equivalent to 11/20 but with a denominator of 100. To achieve this, we can set up a proportion:
11/20 = x/100
Solving for 'x' involves cross-multiplication:
20x = 1100
x = 1100/20
x = 55
This confirms that 11/20 is equivalent to 55/100, which directly translates to 55%.
Practical Applications and Real-World Examples
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Sales and Discounts: A store offers a 11/20 discount on an item. Knowing that 11/20 is 55%, you can easily calculate the discount amount.
-
Statistics and Data Analysis: Percentages are widely used to represent proportions and probabilities in data analysis. Understanding fraction-to-percentage conversion helps in interpreting statistical findings.
-
Financial Calculations: Calculating interest rates, tax rates, and profit margins often involves converting fractions to percentages.
-
Grade Calculations: If you score 11 out of 20 on a test, your percentage score is 55%.
-
Recipe Scaling: Adjusting recipe ingredients often involves scaling up or down using fractions and percentages.
Alternative Methods for Conversion
While the division method is straightforward, there are alternative approaches to convert fractions to percentages:
-
Using a Calculator: Most calculators have a percentage function that directly converts fractions to percentages. Simply enter the fraction (11/20) and use the percentage function.
-
Mental Math (for simpler fractions): For some fractions, you might be able to mentally convert them to percentages if you recognize their decimal equivalents. For example, 1/2 = 50%, 1/4 = 25%, 3/4 = 75%, etc.
Understanding the Context: Why is this Important?
The ability to confidently convert fractions to percentages extends beyond simple arithmetic. It demonstrates a deeper understanding of numerical relationships and proportional reasoning. This skill is essential for:
- Problem-Solving: It enables efficient and accurate problem-solving in diverse contexts.
- Data Interpretation: Understanding percentages is crucial for interpreting data presented in various forms.
- Critical Thinking: It allows for critical analysis of information and making informed decisions based on numerical data.
Frequently Asked Questions (FAQs)
Q1: Can all fractions be converted to percentages?
A: Yes, all fractions can be converted to percentages. This is because any fraction can be expressed as a decimal, and any decimal can be expressed as a percentage.
Q2: What if the fraction results in a repeating decimal?
A: If the division results in a repeating decimal (for example, 1/3 = 0.333...), you can round the decimal to a suitable number of decimal places before converting it to a percentage.
Q3: How do I convert a percentage back to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 55% = 55/100 = 11/20.
Q4: What are some common percentage equivalents of fractions?
A: It's helpful to memorize some common equivalents:
- 1/2 = 50%
- 1/4 = 25%
- 3/4 = 75%
- 1/5 = 20%
- 1/10 = 10%
- 1/100 = 1%
Q5: Are there any online tools to help with fraction-to-percentage conversion?
A: Yes, many websites and online calculators can perform this conversion automatically. However, understanding the underlying principles is crucial for a deeper comprehension of the mathematics involved.
Conclusion: Mastering Fraction-to-Percentage Conversion
Converting 11/20 to a percentage, resulting in 55%, is a straightforward process that involves dividing the numerator by the denominator and multiplying the result by 100. However, this simple calculation represents a much larger concept—a cornerstone of mathematical understanding with far-reaching applications in various aspects of life. By mastering this skill, you equip yourself with a powerful tool for problem-solving, data interpretation, and critical thinking. The ability to confidently convert fractions to percentages is not just about numbers; it's about understanding relationships, proportions, and the language of data. This skill, once mastered, will undoubtedly serve you well throughout your academic and professional life.
Latest Posts
Latest Posts
-
What Is 44cm In Inches
Sep 23, 2025
-
Story About Akbar And Birbal
Sep 23, 2025
-
Of The Body 8 Letters
Sep 23, 2025
-
Improve Crossword Clue 7 Letters
Sep 23, 2025
-
1500 Sq Feet To Meters
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 11 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.