13 10 As A Decimal
elan
Sep 15, 2025 · 6 min read
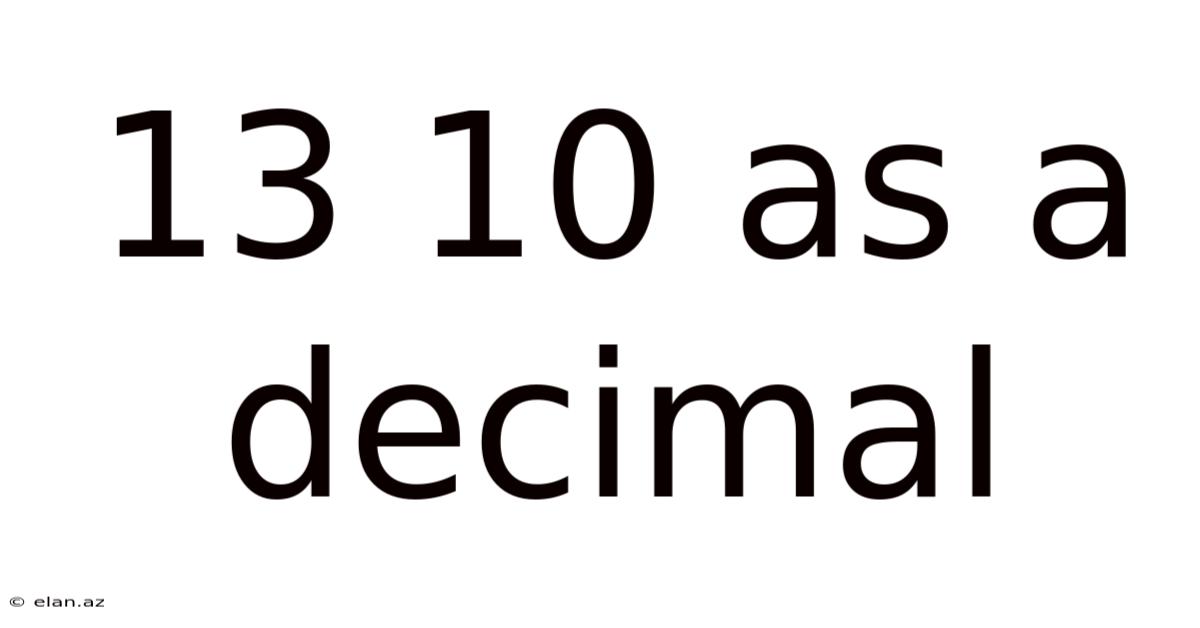
Table of Contents
Understanding 13 10 as a Decimal: A Comprehensive Guide
Converting numbers from different number systems is a fundamental concept in mathematics. This article dives deep into understanding how to represent the number "13 10" as a decimal, exploring the underlying principles, different interpretations, and potential ambiguities. We'll cover various scenarios and provide a clear, step-by-step explanation suitable for learners of all levels. Understanding this seemingly simple conversion opens doors to more complex mathematical operations and strengthens your foundation in numerical representation.
What Does "13 10" Even Mean?
Before we begin the conversion process, it's crucial to address the inherent ambiguity in the notation "13 10". This representation lacks clarity regarding its intended number system. Is it:
- A mixed number? This interpretation suggests 13 and 10/x, where 'x' represents an unspecified denominator. Without knowing 'x', we cannot perform a conversion.
- Two separate numbers? This implies two distinct numbers, 13 and 10, with no defined relationship.
- A number in a non-decimal base? Perhaps "13" and "10" represent digits in a base other than 10 (our standard decimal system). This possibility requires further investigation.
To proceed accurately, we must assume a specific context or clarify the representation's meaning. Let's explore the most likely scenarios.
Scenario 1: 13 10 as a Mixed Number (Base 10)
This interpretation assumes "13 10" represents a mixed number in base 10 – specifically, 13 and 10/x. However, without knowing the value of 'x' (the denominator), we cannot accurately convert it to a decimal. We need more information to define the fraction portion. For example, if x were 100, then 13 10 would mean 13 + 10/100 = 13.1. If x were 1, it would be 13+10 = 23. This scenario highlights the importance of clear notation.
Scenario 2: 13 10 as Two Separate Decimal Numbers
If we treat 13 and 10 as separate decimal numbers, there's no direct conversion needed. They are already expressed in base 10. However, we can perform operations on them:
- Addition: 13 + 10 = 23
- Subtraction: 13 - 10 = 3
- Multiplication: 13 * 10 = 130
- Division: 13 / 10 = 1.3; 10 / 13 ≈ 0.769
The operation performed will determine the resulting decimal value. Without knowing the intended arithmetic operation, a single decimal equivalent is impossible to determine.
Scenario 3: 13 10 as a Number in a Non-Decimal Base
This scenario assumes "13" and "10" represent digits within a base other than 10. Let's explore the most common alternatives:
-
Base 12 (Duodecimal): In base 12, the digits range from 0 to 11. The number "13" would not be valid in base 12, as it uses a digit beyond the permitted range. Similarly, "10" is a valid number representing 12 in base 10.
-
Base 16 (Hexadecimal): Similarly to base 12, base 16 uses digits from 0-15, commonly represented as 0-9 and A-F. The numbers "13" and "10" are valid hexadecimal numbers. Let's convert them to decimal:
- 13 (hexadecimal) = 116¹ + 316⁰ = 16 + 3 = 19 (decimal)
- 10 (hexadecimal) = 116¹ + 016⁰ = 16 + 0 = 16 (decimal)
Again, the meaning depends on the operation. Addition would result in 19 + 16 = 35 (decimal).
-
Other Bases: Similar conversions can be performed for other bases. The general formula for converting a number from base b to base 10 is:
(d<sub>n</sub> * b<sup>n</sup>) + (d<sub>n-1</sub> * b<sup>n-1</sup>) + ... + (d<sub>1</sub> * b<sup>1</sup>) + (d<sub>0</sub> * b<sup>0</sup>)
where:
- d<sub>i</sub> are the digits of the number in base b
- b is the base
- n is the highest power of b
Therefore, it's vital to specify the base when dealing with numbers not written in base 10.
Detailed Example: Converting from Base 16 to Base 10
Let's convert the hexadecimal number A2F to decimal. Remember that A represents 10, B represents 11, C represents 12, D represents 13, E represents 14, and F represents 15 in the hexadecimal system.
-
Identify the digits and their place values:
- A (10) is in the 16² place (256)
- 2 is in the 16¹ place (16)
- F (15) is in the 16⁰ place (1)
-
Perform the calculation:
(10 * 16²) + (2 * 16¹) + (15 * 16⁰) = (10 * 256) + (2 * 16) + (15 * 1) = 2560 + 32 + 15 = 2607
Therefore, the hexadecimal number A2F is equal to 2607 in decimal.
Common Mistakes and How to Avoid Them
Several common mistakes can arise when working with number bases:
- Confusing the base: Always clearly identify the base of the number you're working with.
- Incorrect digit values: Ensure you're using the correct digit values for the specified base.
- Arithmetic errors: Carefully perform the calculations to avoid mistakes in the conversion process.
- Assuming a base without confirmation: This is the most common mistake and why specifying the base is so crucial.
Paying careful attention to these points will help you avoid errors and ensure accurate conversions.
Frequently Asked Questions (FAQs)
Q1: What is the difference between a decimal and a binary number?
A1: A decimal number uses base 10 (digits 0-9), while a binary number uses base 2 (digits 0-1). Binary is frequently used in computer science.
Q2: How can I convert a decimal number to another base?
A2: To convert a decimal number to another base (let's say base b), repeatedly divide the decimal number by b and record the remainders. The remainders, read in reverse order, form the representation of the number in base b.
Q3: What if the number "13 10" represents a coordinate?
A3: In this context, "13 10" would represent a point on a two-dimensional plane, where 13 is the x-coordinate and 10 is the y-coordinate. This has nothing to do with a direct numerical base conversion.
Q4: Are there other number systems besides decimal, binary, and hexadecimal?
A4: Yes! There are numerous number systems, including octal (base 8), ternary (base 3), and many more, each with its specific applications and uses.
Conclusion
Converting "13 10" to a decimal value depends entirely on the context of the notation. It is not a uniquely solvable problem without further information. If "13 10" represents two separate decimal numbers, it requires a defined arithmetic operation. If it represents a number in a non-decimal base, the base must be specified. Understanding different number systems, the potential for ambiguity in notation, and the importance of specifying the base is paramount for accurate mathematical operations and avoids confusion. This article provided a robust explanation for various interpretations of "13 10," emphasizing the need for clear communication and a strong understanding of base conversion principles. Remember that the core of this topic lies in precision and attention to detail. Mastering these concepts forms a strong foundation for further exploration of mathematical ideas.
Latest Posts
Latest Posts
-
Step Up Step Down Transformer
Sep 15, 2025
-
Group Of Six Crossword Clue
Sep 15, 2025
-
Toy Demonstrating Archimedes Buoyancy Principle
Sep 15, 2025
-
35 Percent As A Fraction
Sep 15, 2025
-
Malt With Cod Liver Oil
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 13 10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.