15 22 As A Percentage
elan
Sep 20, 2025 · 5 min read
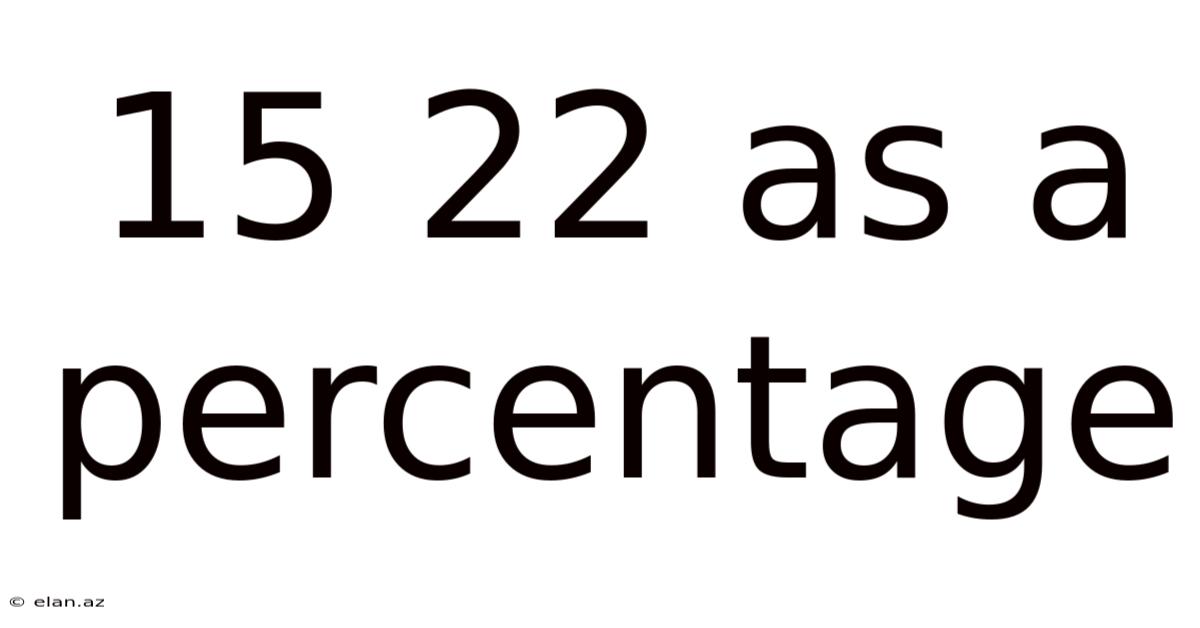
Table of Contents
Decoding 15 out of 22: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex scientific calculations. This article dives deep into calculating the percentage that 15 represents out of 22, explaining the method step-by-step, exploring the underlying mathematical principles, and addressing common questions surrounding percentage calculations. We'll also examine practical applications and explore how to perform these calculations using different methods, making this a comprehensive resource for anyone seeking to master percentage computations.
Understanding the Basics of Percentages
Before we tackle the specific problem of "15 out of 22 as a percentage," let's establish a firm grasp of fundamental percentage concepts. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
The core formula for calculating a percentage is:
(Part / Whole) * 100% = Percentage
Where:
- Part: Represents the specific portion you're interested in expressing as a percentage.
- Whole: Represents the total amount or the complete quantity.
- Percentage: The resulting value expressing the part as a fraction of the whole, represented as a percentage.
Calculating 15 out of 22 as a Percentage: A Step-by-Step Guide
Now, let's apply this formula to determine what percentage 15 represents out of 22.
Step 1: Identify the Part and the Whole
In our problem, the Part is 15, and the Whole is 22.
Step 2: Substitute the Values into the Formula
We substitute these values into our formula:
(15 / 22) * 100% = Percentage
Step 3: Perform the Calculation
First, divide 15 by 22:
15 / 22 ≈ 0.6818
Next, multiply the result by 100%:
0.6818 * 100% ≈ 68.18%
Step 4: Rounding the Result
The result, 68.18%, can be rounded to the desired level of precision. For most practical purposes, rounding to one or two decimal places is sufficient. Therefore, 15 out of 22 is approximately 68.18%.
Different Methods for Calculating Percentages
While the formula (Part / Whole) * 100% is the most straightforward method, other approaches can be equally effective, particularly when dealing with more complex scenarios or when using calculators or software.
-
Using a Calculator: Most calculators have a percentage function (%) which simplifies the calculation. You simply enter 15 ÷ 22 × 100 and press the % button, resulting directly in 68.18%.
-
Using Proportions: This method is useful for understanding the underlying relationship between the parts and the whole. You set up a proportion:
15/22 = x/100
Solving for x (the percentage) involves cross-multiplication:
22x = 1500
x = 1500/22 ≈ 68.18%
- Using Decimal Conversion: Convert the fraction to a decimal (15/22 ≈ 0.6818) and then multiply by 100 to obtain the percentage (0.6818 * 100 = 68.18%).
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations.
-
Science: Percentages are frequently used to express experimental results, statistical data, and measurement uncertainties. For example, expressing the percentage of a certain element in a compound or the percentage change in a population.
-
Education: Grading systems, test scores, and performance evaluations often utilize percentages to represent achievement levels.
-
Retail: Discounts, sales tax, and profit margins are all calculated using percentages.
-
Everyday Life: Calculating tips, understanding nutritional information on food labels, and interpreting statistical data in news reports all involve percentages.
Expanding on the Concept: Percentage Increase and Decrease
While this article primarily focuses on calculating the percentage one number represents of another, it's important to also understand percentage increases and decreases. These concepts involve calculating the change in a quantity as a percentage of the original quantity.
- Percentage Increase: This involves calculating the percentage change when a quantity increases. The formula is:
[(New Value - Original Value) / Original Value] * 100%
- Percentage Decrease: This involves calculating the percentage change when a quantity decreases. The formula is:
[(Original Value - New Value) / Original Value] * 100%
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage with a larger or smaller whole number?
A: The process remains the same. Simply replace the "Part" and "Whole" values in the formula (Part/Whole) * 100% with your specific numbers and perform the calculation.
Q: How do I handle rounding errors?
A: Rounding errors are inherent in many calculations. It's important to maintain consistency in your rounding method (e.g., rounding to two decimal places) throughout your calculations. For extremely precise results, consider using software or tools capable of handling high-precision numbers.
Q: Can I calculate percentages with negative numbers?
A: Yes, you can. However, interpreting the results requires careful consideration of the context. Negative percentages often signify a decrease or loss.
Q: Are there any online calculators for percentage calculations?
A: Yes, numerous online calculators are available that can perform percentage calculations automatically, saving you the manual calculations. However, understanding the underlying principles remains crucial for proper interpretation of the results.
Conclusion: Mastering Percentage Calculations
Calculating percentages is a fundamental mathematical skill that finds applications across various aspects of life. Understanding the formula, (Part/Whole) * 100%, and the steps involved allows for accurate and efficient calculation. By mastering this skill, you'll be better equipped to analyze data, interpret information, and make informed decisions in various contexts—from your personal finances to your professional endeavors. Remember that while calculators and online tools can assist with the computation, a solid understanding of the underlying concepts remains essential for accurate interpretation and application of percentage calculations. This comprehensive guide serves as a valuable resource, enabling you to confidently tackle percentage problems and apply this essential skill in your daily life.
Latest Posts
Latest Posts
-
Words That Start With Za
Sep 20, 2025
-
How To Subtract Mixed Fractions
Sep 20, 2025
-
X 3 X 1 4
Sep 20, 2025
-
Difference Between Immigration And Migration
Sep 20, 2025
-
How Long Is 24 Inches
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 15 22 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.