17 30 As A Percentage
elan
Sep 18, 2025 · 5 min read
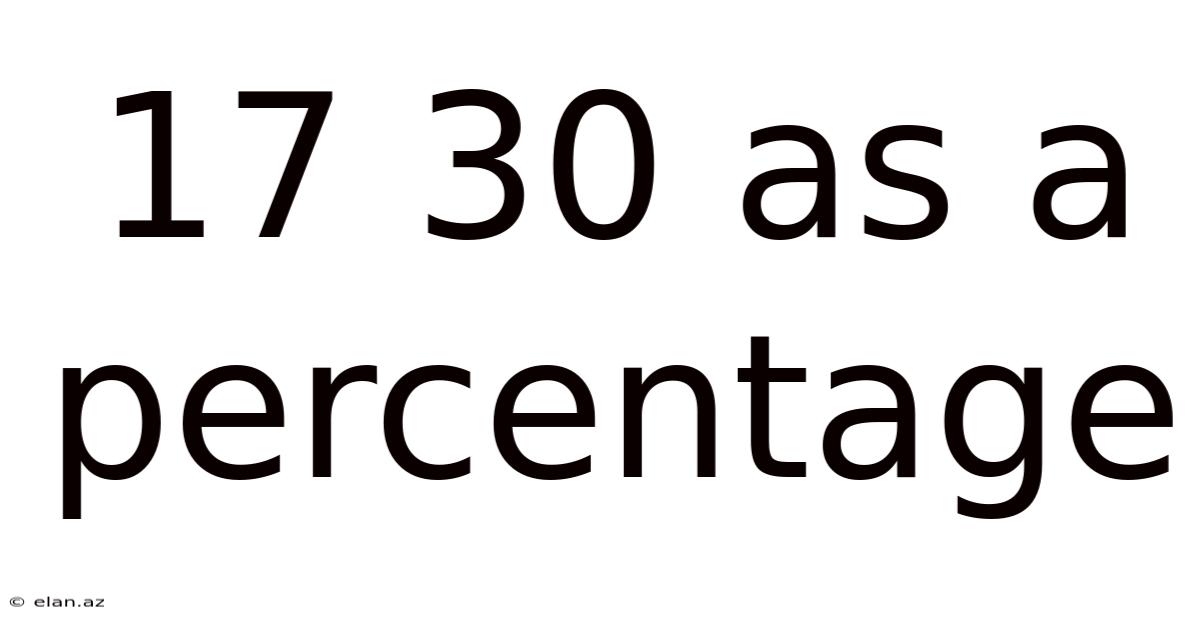
Table of Contents
17/30 as a Percentage: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from everyday budgeting to complex scientific calculations. This article provides a comprehensive guide on converting the fraction 17/30 into a percentage, explaining the process step-by-step and exploring the broader concepts involved. We'll delve into the underlying mathematics, offer multiple approaches to solve the problem, and address frequently asked questions to ensure a complete understanding of this crucial concept.
Understanding Fractions and Percentages
Before we tackle the conversion of 17/30, let's briefly review the basics of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For instance, in the fraction 17/30, 17 represents the parts we're interested in, and 30 represents the total number of parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of 100. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or 1/2.
Converting 17/30 to a Percentage: The Primary Method
The most straightforward method to convert a fraction to a percentage involves two simple steps:
Step 1: Convert the fraction to a decimal.
To do this, divide the numerator (17) by the denominator (30):
17 ÷ 30 = 0.566666...
The result is a recurring decimal, meaning the digit 6 repeats infinitely. We'll address how to handle this precision issue shortly.
Step 2: Convert the decimal to a percentage.
Multiply the decimal by 100:
0.566666... × 100 = 56.6666...%
Therefore, 17/30 is approximately 56.67%. The rounding to two decimal places is a common practice for percentages, offering sufficient accuracy for most applications.
Handling Recurring Decimals: Precision and Rounding
As you've seen, the conversion of 17/30 leads to a recurring decimal. The accuracy of the percentage depends on how many decimal places you retain. While we rounded to 56.67% for practical purposes, it's important to understand the implications of rounding:
-
Rounding Error: Rounding introduces a small error. The more decimal places you retain, the smaller the error. However, for most everyday calculations, two decimal places are sufficient.
-
Exact Representation: To represent the exact value, you would need to use the recurring decimal notation (56.666...%) or express it as a fraction (17/30).
Alternative Methods for Conversion
While the primary method is the most common, there are alternative approaches to convert 17/30 to a percentage:
Method 2: Using Proportions
This method uses the concept of proportions. We know that a percentage is a fraction out of 100. We can set up a proportion:
17/30 = x/100
To solve for x (the percentage), cross-multiply:
30x = 1700
x = 1700/30 = 56.666...
Again, we arrive at the approximate percentage of 56.67%.
Method 3: Scaling to 100
This method involves finding an equivalent fraction with a denominator of 100. This requires finding a number to multiply both the numerator and denominator of 17/30 to achieve a denominator of 100. Unfortunately, there is no whole number that will allow us to do this exactly. This highlights why the division method is generally preferred for fractions that don't easily scale to 100.
The Importance of Understanding Percentage Calculations
The ability to convert fractions to percentages is crucial for various reasons:
-
Financial Literacy: Understanding percentages is essential for managing personal finances, calculating interest rates, discounts, taxes, and tips.
-
Data Analysis: Percentages are widely used in data analysis to represent proportions, trends, and changes in data sets. Graphs and charts often use percentages to visually represent data.
-
Scientific Applications: Percentages are used extensively in scientific fields to express concentrations, yields, and statistical probabilities.
Frequently Asked Questions (FAQ)
Q1: What if the fraction has a larger numerator than denominator?
A1: If the numerator is larger than the denominator, the fraction is greater than 1. When converting to a percentage, the resulting percentage will be greater than 100%. For example, 30/17 as a percentage is (30/17)*100 ≈ 176.47%
Q2: Can I use a calculator for these conversions?
A2: Absolutely! Calculators are a valuable tool for these calculations, especially when dealing with complex fractions or recurring decimals. Most calculators have a percentage function that simplifies the process.
Q3: Why do we round percentages?
A3: We round percentages for practicality and to avoid excessively long decimal places. The level of precision needed depends on the context. In many cases, two decimal places offer a sufficient level of accuracy.
Q4: Are there any online tools to convert fractions to percentages?
A4: Yes, many online calculators and converters are available to perform this conversion quickly and easily. However, understanding the underlying mathematical process is crucial for true comprehension.
Conclusion
Converting 17/30 to a percentage involves dividing the numerator by the denominator and then multiplying the result by 100. This yields approximately 56.67%. Understanding the different methods for conversion and the implications of recurring decimals provides a more complete understanding of this fundamental mathematical concept. The ability to perform this conversion is vital for various applications in everyday life and across different disciplines. Mastering this skill enhances numerical literacy and problem-solving abilities. This comprehensive guide aims to not only provide the solution but also to build a strong foundational understanding of fraction-to-percentage conversion, empowering you to tackle similar problems with confidence.
Latest Posts
Latest Posts
-
Direct Current Or Alternating Current
Sep 18, 2025
-
Words With X 2 Letter
Sep 18, 2025
-
Spelling Words For Year 3
Sep 18, 2025
-
Example Of An Energy Transfer
Sep 18, 2025
-
Words That Start With Ti
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 17 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.