18 24 In Simplest Form
elan
Sep 20, 2025 · 6 min read
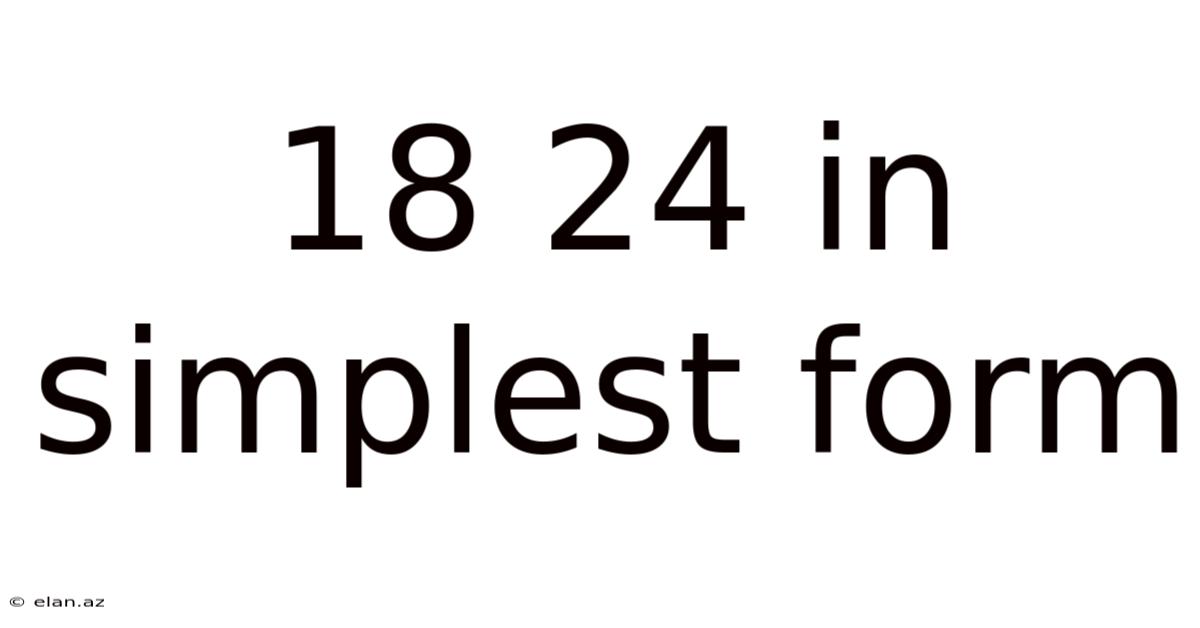
Table of Contents
Simplifying 18/24: A Comprehensive Guide to Fractions
Understanding fractions is a fundamental skill in mathematics, forming the bedrock for more advanced concepts. This article will delve into the simplification of the fraction 18/24, explaining the process in a clear and accessible manner, suitable for learners of all levels. We'll explore the concept of greatest common divisors (GCD), provide step-by-step instructions, and address frequently asked questions to ensure a complete understanding of fraction simplification. This guide will cover not only how to simplify 18/24 but also why the process works, building a strong foundation in mathematical reasoning.
Introduction to Fractions and Simplification
A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 18/24, 18 is the numerator and 24 is the denominator. This fraction indicates 18 parts out of a total of 24 parts.
Simplifying a fraction, also known as reducing a fraction to its lowest terms, means finding an equivalent fraction with a smaller numerator and denominator. This simplified fraction represents the same value as the original fraction but is expressed in its most concise form. Simplifying fractions is crucial for several reasons: it makes calculations easier, improves readability, and provides a clearer understanding of the proportion represented.
Finding the Greatest Common Divisor (GCD)
The key to simplifying fractions lies in finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. There are several ways to find the GCD:
-
Listing Factors: List all the factors (numbers that divide evenly) of both the numerator and denominator. Then, identify the largest factor they have in common.
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- The common factors are 1, 2, 3, and 6. The greatest common factor is 6.
-
Prime Factorization: Break down both the numerator and denominator into their prime factors (numbers divisible only by 1 and themselves). The GCD is the product of the common prime factors raised to the lowest power.
- 18 = 2 x 3 x 3 = 2 x 3²
- 24 = 2 x 2 x 2 x 3 = 2³ x 3
- The common prime factors are 2 and 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3¹. Therefore, the GCD is 2 x 3 = 6.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 24 by 18: 24 = 18 x 1 + 6
- Divide 18 by the remainder 6: 18 = 6 x 3 + 0
- The last non-zero remainder is 6, so the GCD is 6.
Step-by-Step Simplification of 18/24
Now that we've established the GCD of 18 and 24 is 6, we can simplify the fraction:
-
Identify the GCD: As determined above, the GCD of 18 and 24 is 6.
-
Divide both the numerator and denominator by the GCD:
- Numerator: 18 ÷ 6 = 3
- Denominator: 24 ÷ 6 = 4
-
Write the simplified fraction: The simplified fraction is 3/4.
Therefore, 18/24 simplified to its lowest terms is 3/4.
Visual Representation of Fraction Simplification
Imagine you have a pizza cut into 24 slices. The fraction 18/24 represents having 18 of those 24 slices. To simplify, we can group the slices. If we group the slices into sets of 6, we'll have 3 groups of 6 slices out of a total of 4 groups of 6 slices. This visually demonstrates how 18/24 is equivalent to 3/4.
Further Applications and Advanced Concepts
The ability to simplify fractions is essential for various mathematical operations:
-
Addition and Subtraction of Fractions: Before adding or subtracting fractions, they must have a common denominator. Simplifying fractions often makes finding a common denominator easier.
-
Multiplication and Division of Fractions: Simplifying fractions before performing multiplication or division can significantly reduce the complexity of the calculations. It allows you to cancel out common factors, simplifying the process.
-
Solving Equations: Many equations involve fractions. Simplifying fractions within these equations helps to make them more manageable and easier to solve.
-
Ratios and Proportions: Fractions are fundamental to understanding ratios and proportions. Simplifying fractions allows for a clearer and more concise representation of these relationships.
Frequently Asked Questions (FAQ)
Q: What if I don't find the greatest common divisor?
A: If you don't find the greatest common divisor initially, you can still simplify the fraction by dividing the numerator and denominator by any common factor. You'll just need to repeat the process until you reach the simplest form. For example, you could divide 18/24 by 2 initially, resulting in 9/12. Then you could divide by 3, resulting in 3/4.
Q: Is there a way to check if a fraction is in its simplest form?
A: Once you've simplified a fraction, you can check if it's in its simplest form by ensuring that the GCD of the numerator and denominator is 1. If the only common factor is 1, the fraction is in its simplest form.
Q: What if the numerator is larger than the denominator?
A: If the numerator is larger than the denominator, the fraction is called an improper fraction. You can simplify improper fractions in the same way as proper fractions (where the numerator is smaller than the denominator). You can also convert an improper fraction into a mixed number (a whole number and a proper fraction). For example, the improper fraction 24/18 simplifies to 4/3, which is equivalent to the mixed number 1 1/3.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes calculations easier and more efficient. It allows for a clearer understanding of the proportion represented, and it's a crucial skill for more advanced mathematical concepts.
Conclusion: Mastering Fraction Simplification
Simplifying fractions, as demonstrated with the example of 18/24, is a straightforward yet crucial skill in mathematics. By understanding the concept of the greatest common divisor and applying the steps outlined above, you can confidently simplify any fraction. Mastering this skill not only improves your mathematical abilities but also provides a strong foundation for tackling more complex problems in algebra, calculus, and other advanced mathematical fields. Remember, practice is key to mastering this fundamental concept! Work through several examples to solidify your understanding and build confidence in your ability to simplify fractions. The more you practice, the easier and faster it will become.
Latest Posts
Latest Posts
-
Usb 2 V Usb 3
Sep 20, 2025
-
What Can The Matter Be
Sep 20, 2025
-
Two Letter Words With X
Sep 20, 2025
-
Example Of An Acute Disease
Sep 20, 2025
-
Fmcg What Does It Mean
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 18 24 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.