18 30 As A Percentage
elan
Sep 17, 2025 · 5 min read
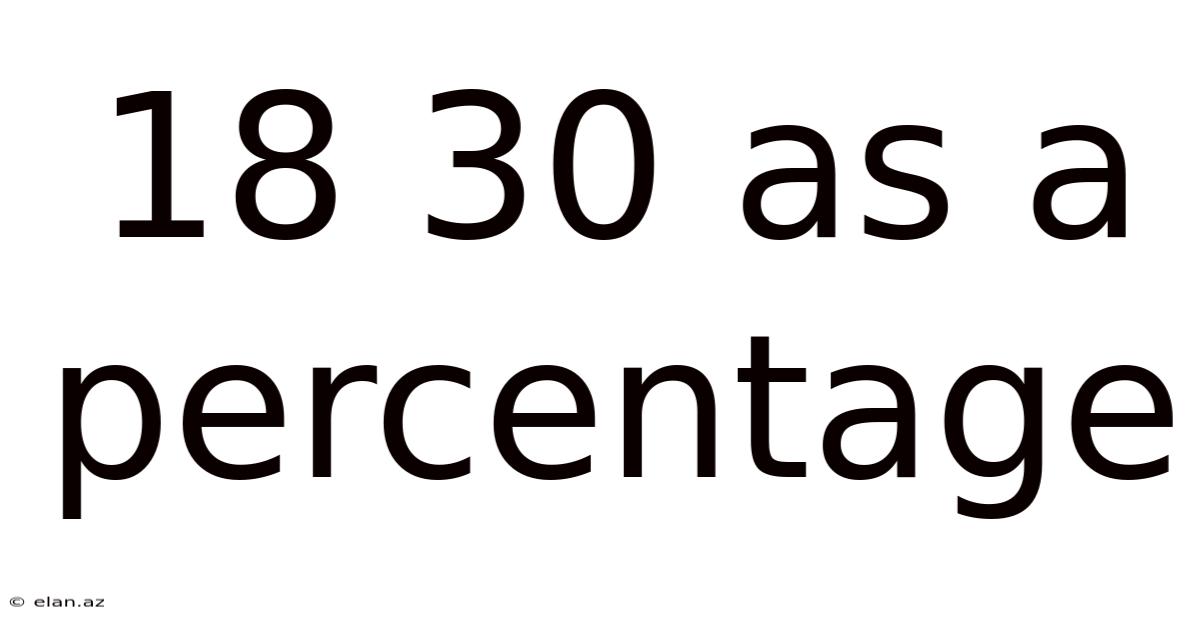
Table of Contents
18/30 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analysis. This comprehensive guide will delve into calculating 18/30 as a percentage, explaining the process step-by-step and exploring the broader context of percentage calculations. We will cover different methods, address common misconceptions, and even explore the application of this specific calculation in real-world scenarios. By the end, you'll not only know the answer but also possess a deeper understanding of percentage calculations.
Understanding Percentages: The Fundamentals
A percentage represents a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." To express a fraction or decimal as a percentage, we simply multiply it by 100 and add the "%" symbol. Conversely, to convert a percentage to a decimal, we divide it by 100.
For instance, 50% represents 50/100, which simplifies to 1/2 or 0.5. Similarly, 0.75 is equivalent to 75/100 or 75%.
Calculating 18/30 as a Percentage: Method 1 (Fraction to Decimal to Percentage)
The most straightforward approach involves converting the fraction 18/30 to a decimal first and then to a percentage.
-
Simplify the Fraction: Before converting, simplify the fraction if possible. 18/30 can be simplified by dividing both the numerator (18) and the denominator (30) by their greatest common divisor (GCD), which is 6. This simplifies the fraction to 3/5.
-
Convert the Fraction to a Decimal: To convert the simplified fraction 3/5 to a decimal, divide the numerator (3) by the denominator (5): 3 ÷ 5 = 0.6
-
Convert the Decimal to a Percentage: Multiply the decimal (0.6) by 100 and add the percentage symbol (%): 0.6 * 100 = 60%.
Therefore, 18/30 is equal to 60%.
Calculating 18/30 as a Percentage: Method 2 (Direct Percentage Calculation)
Alternatively, we can directly calculate the percentage without simplifying the fraction first.
-
Set up the Proportion: We can set up a proportion to solve for the percentage:
18/30 = x/100
Where 'x' represents the percentage we want to find.
-
Cross-Multiply: Cross-multiply to solve for 'x':
30x = 18 * 100 30x = 1800
-
Solve for x: Divide both sides by 30:
x = 1800 ÷ 30 x = 60
Therefore, x = 60%, confirming our previous result.
Understanding the Significance of 60%
A score of 60% generally represents a passing grade in many educational systems. However, the interpretation of 60% depends heavily on the context.
-
Academic Performance: In an academic setting, 60% might be considered a satisfactory or passing grade, but it doesn't necessarily indicate excellence. It suggests a basic understanding of the material.
-
Business and Finance: In business and finance, 60% could represent a significant portion of a market share, a profit margin, or a completion rate for a project. Its significance varies depending on the specific industry and target.
-
Surveys and Statistics: In surveys and statistical analyses, 60% indicates a considerable portion of a sample population holding a specific opinion or exhibiting a particular characteristic.
Common Misconceptions about Percentage Calculations
Several common errors can arise when dealing with percentages:
-
Confusing Percentage Change with Percentage Points: A change from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage itself. This distinction is crucial in interpreting percentage changes accurately.
-
Incorrect Order of Operations: When performing multiple calculations involving percentages, it's vital to follow the correct order of operations (PEMDAS/BODMAS).
-
Improperly Handling Percentages of Percentages: Calculating percentages of percentages requires careful attention to ensure the calculations are performed correctly. For example, a 10% discount on an item already discounted by 20% is not a 30% discount.
Advanced Applications of Percentage Calculations
Beyond the basic calculations, percentages are used in:
-
Compound Interest: Calculating compound interest involves repeated application of percentage calculations.
-
Financial Modeling: Percentages are crucial in financial modeling to project future earnings, expenses, and investment returns.
-
Statistical Analysis: Percentages are essential for summarizing and interpreting statistical data.
-
Data Visualization: Percentages are frequently used in charts and graphs to present data clearly and concisely.
Frequently Asked Questions (FAQs)
Q: Can I calculate percentages using a calculator?
A: Yes, most calculators have a percentage function (%) that simplifies the calculation. You can either directly input the fraction (e.g., 18/30) or convert it to a decimal first and then use the percentage function.
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new and old values, divide the difference by the old value, and multiply by 100. For a percentage decrease, the process is the same but with a negative result indicating a decrease.
Q: What if the denominator is zero?
A: Dividing by zero is undefined. You cannot calculate a percentage if the denominator of the fraction is zero.
Q: How do I calculate the percentage of a specific value?
A: To find the percentage of a value, multiply the value by the percentage (expressed as a decimal). For example, to find 25% of 80, you would calculate 0.25 * 80 = 20.
Conclusion
Calculating 18/30 as a percentage is a simple yet illustrative example of applying fundamental mathematical concepts. Understanding percentages is not just about performing calculations; it's about interpreting and applying this knowledge effectively across various contexts. By grasping the fundamentals and avoiding common pitfalls, you'll enhance your numeracy skills and improve your ability to analyze and interpret data in diverse situations. Remember, the key is to approach percentage calculations methodically, whether using the direct method or a step-by-step approach of converting fractions to decimals and then to percentages. This understanding empowers you to confidently tackle more complex percentage-based problems in your academic pursuits, professional endeavors, and everyday life.
Latest Posts
Latest Posts
-
Synaptic Transmission A Level Biology
Sep 17, 2025
-
Capitals Of All European Countries
Sep 17, 2025
-
Liquids On The Periodic Table
Sep 17, 2025
-
Aerobic And Anaerobic Respiration Equation
Sep 17, 2025
-
Advantages And Disadvantages Star Topology
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 18 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.