18 40 As A Percentage
elan
Sep 17, 2025 · 5 min read
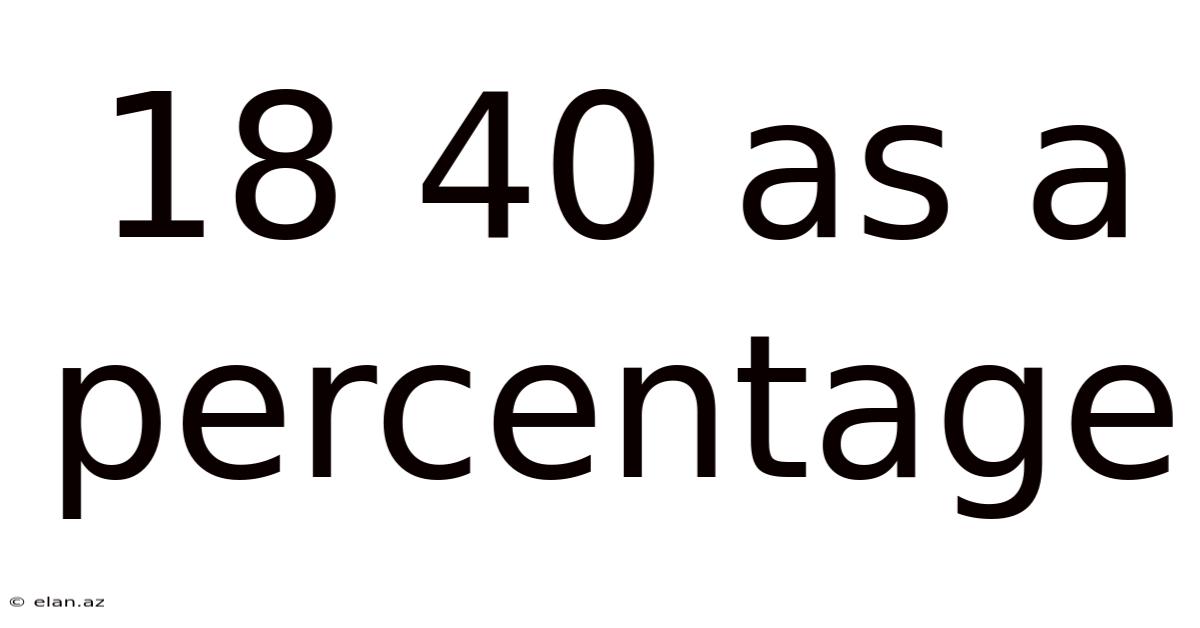
Table of Contents
Understanding 18/40 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday life. This article delves into the process of converting the fraction 18/40 into a percentage, explaining the steps involved, providing practical examples, and exploring the broader concept of percentage calculations. We'll also cover related concepts and frequently asked questions to ensure a comprehensive understanding.
Introduction: From Fractions to Percentages
A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "out of one hundred." Converting a fraction like 18/40 to a percentage involves finding the equivalent fraction with a denominator of 100, then expressing the numerator as a percentage. This process is crucial for understanding proportions, ratios, and various real-world applications involving comparisons and proportions. Mastering this skill provides a strong foundation for more advanced mathematical concepts.
Method 1: Direct Conversion using Division
The most straightforward method for converting 18/40 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (18) by the denominator (40). 18 ÷ 40 = 0.45
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add a percentage sign (%). 0.45 x 100 = 45%
Therefore, 18/40 is equivalent to 45%.
Method 2: Simplifying the Fraction First
While the direct division method is efficient, simplifying the fraction before conversion can sometimes make the calculation easier. This is particularly helpful when dealing with larger numbers.
-
Find the greatest common divisor (GCD) of the numerator and denominator: The GCD of 18 and 40 is 2.
-
Simplify the fraction by dividing both the numerator and denominator by the GCD: 18 ÷ 2 = 9 40 ÷ 2 = 20
This simplifies the fraction to 9/20.
-
Convert the simplified fraction to a decimal: 9 ÷ 20 = 0.45
-
Convert the decimal to a percentage: 0.45 x 100 = 45%
As you can see, simplifying the fraction first doesn't change the final result; it just provides an alternative approach that might be simpler in certain cases.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We set up a proportion where the fraction 18/40 is equal to x/100, where x represents the percentage we're trying to find.
-
Set up the proportion: 18/40 = x/100
-
Cross-multiply: 18 * 100 = 40 * x 1800 = 40x
-
Solve for x: x = 1800 ÷ 40 x = 45
Therefore, x = 45%, confirming our previous results.
Visual Representation: Understanding the Percentage
Imagine you have 40 apples, and 18 of them are red. To find the percentage of red apples, you would use the same process: 18/40 = 45%. This means 45 out of every 100 apples would be red if the proportion remained consistent. Visualizing the problem in this way can make it more intuitive and easier to grasp.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages is vital in numerous real-world situations:
- Calculating grades: If you answered 18 questions correctly out of 40, your score is 45%.
- Financial analysis: Calculating interest rates, discounts, profit margins, and tax rates all rely on percentage calculations.
- Statistical analysis: Percentages are fundamental to expressing proportions and probabilities in data analysis.
- Everyday comparisons: Comparing prices, sales, and various other metrics often involves percentage changes.
Understanding Percentage Increase and Decrease
While this article focuses on converting a fraction to a percentage representing a part of a whole, it's important to understand related concepts like percentage increase and decrease. These involve calculating the change in a value as a percentage of the original value. For instance, if a price increases from 40 to 45, the percentage increase is calculated as follows:
-
Find the difference: 45 - 40 = 5
-
Divide the difference by the original value: 5 ÷ 40 = 0.125
-
Multiply by 100 to express as a percentage: 0.125 x 100 = 12.5%
Therefore, the price increased by 12.5%.
Advanced Concepts: Percentages and Proportions
The connection between percentages and proportions is fundamental. A percentage is essentially a ratio expressed as a fraction of 100. Understanding proportions allows you to solve for unknown values in various scenarios involving ratios and percentages. For example, if 18 out of 40 students passed an exam, and you have a larger class of 200 students with the same pass rate, you can use proportions to determine how many students would pass in that larger class:
18/40 = x/200
Cross-multiplying and solving for x would reveal the number of students expected to pass in the larger class.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 18/40 to a percentage?
A: Yes, simply divide 18 by 40 and then multiply the result by 100. Most calculators have a percentage function that simplifies this process further.
Q: What if the fraction doesn't simplify easily?
A: Even if the fraction doesn't simplify easily, the direct division method will still work. You can use a calculator to perform the division accurately.
Q: Are there any other methods to convert fractions to percentages?
A: Yes, there are other methods, such as using the concept of equivalent fractions or employing more advanced mathematical techniques, but the methods described in this article are the most commonly used and easily understood.
Q: How can I improve my understanding of percentages?
A: Practice is key. Try converting various fractions to percentages, work through word problems involving percentages, and try visual representations to strengthen your understanding.
Conclusion: Mastering Percentage Calculations
Converting fractions to percentages is a valuable skill with wide-ranging applications. Understanding the different methods for converting fractions like 18/40 to a percentage – whether through direct division, simplifying the fraction first, or utilizing proportions – empowers you to solve various mathematical problems and interpret data more effectively. Through consistent practice and a clear understanding of the underlying concepts, you can build a strong foundation in percentage calculations and apply this skill to numerous real-world scenarios. Remember, the key is not just to get the answer (45%), but to understand the why behind the calculation, enhancing your overall mathematical proficiency.
Latest Posts
Latest Posts
-
Liquids On The Periodic Table
Sep 17, 2025
-
Aerobic And Anaerobic Respiration Equation
Sep 17, 2025
-
Advantages And Disadvantages Star Topology
Sep 17, 2025
-
5 6 As A Decimal
Sep 17, 2025
-
Horse Fly Repellent For Humans
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 18 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.