2 10 As A Percent
elan
Sep 14, 2025 · 6 min read
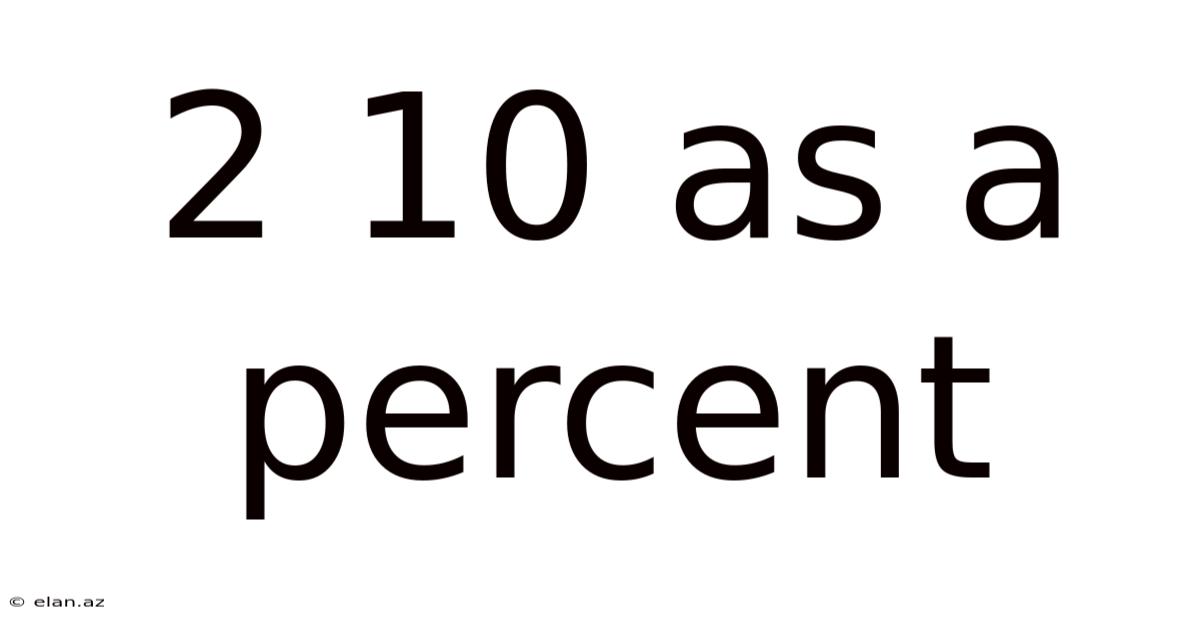
Table of Contents
Understanding 2/10 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and sales tax to understanding financial statements and statistical data. This comprehensive guide will explore how to convert the fraction 2/10 into a percentage, explaining the process step-by-step and delving into the underlying mathematical concepts. We'll also examine practical applications and address frequently asked questions to ensure a thorough understanding of this important concept.
Introduction: Fractions, Decimals, and Percentages – A Unified Perspective
Before we dive into converting 2/10 to a percentage, let's establish a clear understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole. A fraction expresses a part of a whole using a numerator (the top number) and a denominator (the bottom number). A decimal expresses a part of a whole using a base-ten system, with a decimal point separating the whole number from the fractional part. A percentage expresses a part of a whole as a fraction of 100. They are all interconnected and easily convertible from one form to another.
Converting 2/10 to a Percentage: A Step-by-Step Guide
Converting 2/10 to a percentage involves two straightforward steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, you simply divide the numerator by the denominator. In this case:
2 ÷ 10 = 0.2
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent symbol (%). Therefore:
0.2 x 100 = 20%
Therefore, 2/10 is equal to 20%.
Understanding the Concept of Percentage
A percentage represents a proportion out of 100. When we say something is 20%, we mean it represents 20 parts out of every 100 parts. This concept is crucial in various contexts, including:
- Sales and Discounts: A 20% discount means you pay 80% of the original price (100% - 20% = 80%).
- Taxes: Sales tax is often expressed as a percentage of the purchase price.
- Financial Statements: Financial reports frequently utilize percentages to represent ratios, profits, and losses.
- Statistics and Probability: Percentages are used to represent probabilities and proportions in statistical analysis.
- Grade Calculations: Academic grades are often expressed as percentages reflecting the proportion of correct answers.
Practical Applications of 20%
Understanding 20% as a percentage has many practical applications. Here are a few examples:
- Calculating Discounts: If an item is priced at $50 and is offered at a 20% discount, the discount amount is 20% of $50, which is ($50 * 0.20) = $10. The final price would be $40 ($50 - $10).
- Calculating Sales Tax: If the sales tax rate is 20%, and you purchase an item for $100, the tax amount would be ($100 * 0.20) = $20. The total cost would be $120 ($100 + $20).
- Understanding Proportions: Imagine a survey where 20% of 500 respondents answered "yes" to a particular question. This means (500 * 0.20) = 100 respondents answered "yes."
- Financial Analysis: In financial statements, a 20% increase in revenue would indicate significant growth. Conversely, a 20% decrease would signal a decline.
Further Exploration: Converting Other Fractions to Percentages
The process of converting fractions to percentages is consistent regardless of the fraction's complexity. For instance, let's consider converting 3/5 to a percentage:
Step 1: Convert to a Decimal:
3 ÷ 5 = 0.6
Step 2: Convert to a Percentage:
0.6 x 100 = 60%
Therefore, 3/5 is equal to 60%.
We can also handle more complex fractions. Let's take 7/8:
Step 1: Convert to a Decimal:
7 ÷ 8 = 0.875
Step 2: Convert to a Percentage:
0.875 x 100 = 87.5%
Therefore, 7/8 is equal to 87.5%.
This process demonstrates the general method for transforming any fraction into a percentage. The key is to understand the fundamental relationship between fractions, decimals, and percentages, and to apply the steps consistently.
The Importance of Understanding Percentages in Different Contexts
The ability to convert fractions to percentages and to understand the meaning of percentages is crucial in a multitude of fields. Here are some examples:
- Business and Finance: Essential for understanding profit margins, financial ratios, investment returns, and various aspects of financial modeling.
- Science and Engineering: Used extensively in data analysis, experimental results interpretation, and the presentation of scientific findings.
- Healthcare: Used in calculating dosages, interpreting medical test results, and monitoring patient progress.
- Education: Essential for grading, evaluating student performance, and tracking learning outcomes.
- Everyday Life: Helpful in making informed decisions regarding budgeting, shopping, and comparing prices.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to convert a fraction to a percentage?
A1: The easiest way is to first convert the fraction to a decimal by dividing the numerator by the denominator. Then, multiply the decimal by 100 and add the % sign.
Q2: Can I convert a mixed number (a whole number and a fraction) to a percentage?
A2: Yes, you can. First, convert the mixed number into an improper fraction (where the numerator is greater than the denominator). Then, follow the steps outlined above to convert the improper fraction to a percentage.
Q3: What if the fraction results in a repeating decimal when converting to a percentage?
A3: If you encounter a repeating decimal, you can round it to a suitable number of decimal places for practical purposes. For example, 1/3 converts to 0.3333... You can round this to 33.3% or 33.33% depending on the required level of precision.
Q4: Why is understanding percentages important?
A4: Percentages provide a standardized way to compare proportions and make comparisons across different datasets, making data interpretation easier and more intuitive. They are a crucial tool for effective communication of numerical information.
Q5: Are there any online tools to help convert fractions to percentages?
A5: While there are many online calculators available to assist with this conversion, understanding the underlying process is paramount for true comprehension and application in various scenarios.
Conclusion: Mastering the Art of Percentage Conversions
Converting 2/10 to a percentage (20%) is a simple yet fundamental mathematical operation with wide-ranging practical applications. This comprehensive guide has not only detailed the steps involved in this conversion but has also explored the broader concepts of fractions, decimals, and percentages, emphasizing their interconnectedness and importance in various fields. By mastering these concepts, you'll be well-equipped to tackle various real-world problems and confidently navigate quantitative information presented in various formats. Remember, the key is to practice consistently and apply your understanding in diverse contexts to reinforce your knowledge and build your confidence.
Latest Posts
Latest Posts
-
Exact Values For Trig Functions
Sep 14, 2025
-
300 Square Feet To Metres
Sep 14, 2025
-
Is Displacement A Vector Quantity
Sep 14, 2025
-
Words That Start With Mon
Sep 14, 2025
-
Hcf And Lcm Venn Diagram
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 10 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.