2 2/5 As A Decimal
elan
Sep 14, 2025 · 5 min read
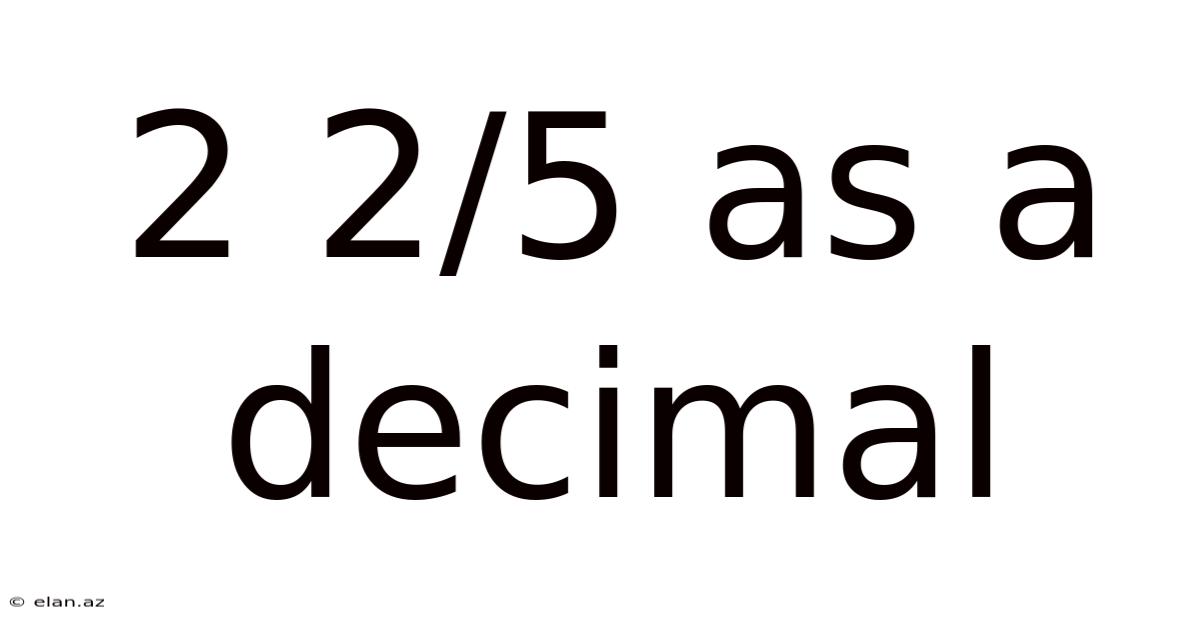
Table of Contents
2 2/5 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 2 2/5 into its decimal equivalent, explaining the underlying principles and providing various methods to solve similar problems. We'll explore different approaches, delve into the reasoning behind each step, and address common questions, making this concept clear and accessible for everyone, from beginners to those looking for a refresher. This guide will equip you with the knowledge and confidence to tackle any fraction-to-decimal conversion.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's quickly review the components of a mixed number like 2 2/5. A mixed number combines a whole number (2 in this case) and a proper fraction (2/5). The whole number represents a complete unit, while the fraction represents a part of a unit. The numerator (2) indicates the number of parts we have, and the denominator (5) indicates the total number of equal parts the unit is divided into.
Method 1: Converting the Fraction to a Decimal, then Adding the Whole Number
This is perhaps the most straightforward method. We'll first convert the fraction 2/5 into a decimal and then add the whole number 2.
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator by the denominator. In this case, we divide 2 by 5:
2 ÷ 5 = 0.4
Step 2: Add the whole number.
Now, we simply add the whole number (2) to the decimal equivalent of the fraction (0.4):
2 + 0.4 = 2.4
Therefore, 2 2/5 as a decimal is 2.4.
Method 2: Converting the Mixed Number to an Improper Fraction, then to a Decimal
This method involves transforming the mixed number into an improper fraction before converting it to a decimal. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
Step 1: Convert the mixed number to an improper fraction.
To convert 2 2/5 to an improper fraction, we multiply the whole number (2) by the denominator (5) and add the numerator (2). This result becomes the new numerator, while the denominator remains the same:
(2 * 5) + 2 = 12
The improper fraction is 12/5.
Step 2: Convert the improper fraction to a decimal.
Now, we divide the numerator (12) by the denominator (5):
12 ÷ 5 = 2.4
Again, we arrive at the same answer: 2 2/5 as a decimal is 2.4.
Method 3: Using the Concept of Place Value
This method emphasizes understanding the place value system in decimals. The fraction 2/5 represents two-fifths of a whole. Since we know that one-fifth (1/5) is equal to 0.2 (because 1 ÷ 5 = 0.2), then two-fifths (2/5) is simply twice that value:
0.2 * 2 = 0.4
Adding the whole number 2, we get:
2 + 0.4 = 2.4
This approach reinforces the connection between fractions and decimals, strengthening your understanding of the underlying principles.
Understanding Decimal Place Value
It’s crucial to understand the place value system in decimals. The number 2.4 can be broken down as follows:
- 2: Represents the whole number, signifying two complete units.
- 4: Represents four-tenths (4/10), indicating a portion of a unit.
This understanding helps interpret the decimal value in the context of the original mixed number.
Why These Methods Work: A Deeper Dive into the Mathematics
The core principle behind all these methods is the fundamental definition of a fraction: it represents a division. A fraction a/b is equivalent to a ÷ b. Therefore, converting a fraction to a decimal always involves performing this division. The methods differ only in their approach to handling the whole number component of a mixed number. Converting to an improper fraction first simplifies the process by dealing with a single fraction before performing the division.
Applying the Knowledge: Converting Other Mixed Numbers
Let's practice with a few more examples to solidify your understanding:
- 3 1/4: 1/4 = 0.25; 3 + 0.25 = 3.25
- 1 3/10: 3/10 = 0.3; 1 + 0.3 = 1.3
- 5 7/8: 7/8 = 0.875; 5 + 0.875 = 5.875
These examples demonstrate how the same principles can be applied consistently to different mixed numbers. Remember to always divide the numerator by the denominator when converting a fraction to a decimal.
Frequently Asked Questions (FAQs)
Q: What if the denominator of the fraction doesn't divide evenly into the numerator?
A: In such cases, the decimal representation will be a repeating decimal or a terminating decimal with many digits. For example, 1/3 = 0.333... (a repeating decimal) while 1/8 = 0.125 (a terminating decimal). You can use long division to find the decimal representation, or a calculator.
Q: Can I use a calculator to convert a mixed number to a decimal?
A: Yes, most calculators can perform this conversion directly. Simply enter the mixed number (e.g., 2 + 2/5 or 12/5) and the calculator will provide the decimal equivalent.
Q: Are there other ways to represent 2 2/5 besides 2.4?
A: While 2.4 is the most common and straightforward decimal representation, you could also represent it as a percentage (240%). The core value remains the same; only the representation changes.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting fractions, particularly mixed numbers, to decimals is a valuable skill with practical applications across various fields. Understanding the underlying mathematical principles and employing different approaches will help you develop a stronger foundation in mathematics. Practice is key to mastering this skill. By working through various examples and applying the methods explained above, you'll gain confidence and proficiency in converting fractions to decimals and vice versa. Remember, the process is straightforward once you grasp the core concept of division inherent in fractions. This skill will not only aid you in academic pursuits but also prove useful in everyday life, from calculating proportions to understanding financial data.
Latest Posts
Latest Posts
-
Logarithm Rules A Level Maths
Sep 14, 2025
-
Perimeter Of Half Circle Calculator
Sep 14, 2025
-
The Schoolboy By William Blake
Sep 14, 2025
-
What Is An Nth Term
Sep 14, 2025
-
Nice Words Start With A
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 2/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.