2 25 As A Percent
elan
Sep 15, 2025 · 5 min read
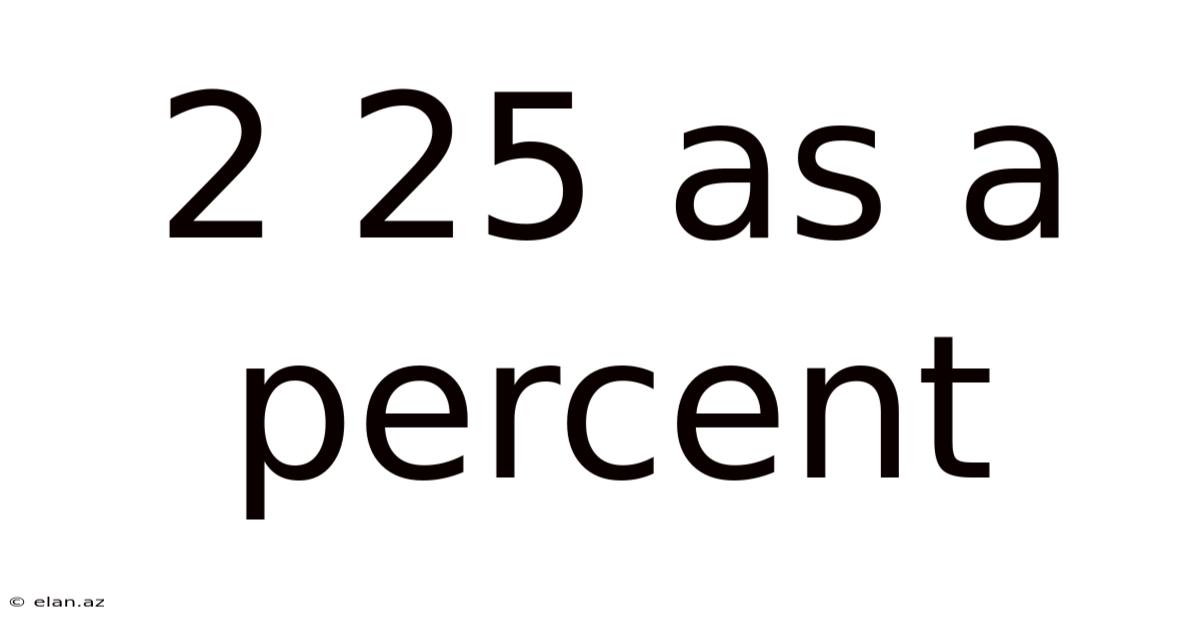
Table of Contents
2/25 as a Percent: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This comprehensive guide will delve into how to convert the fraction 2/25 into a percentage, explaining the process step-by-step and exploring the underlying mathematical concepts. We'll also examine practical applications and address frequently asked questions. This guide aims to not only provide the answer but also build a robust understanding of the principles involved.
Understanding Fractions and Percentages
Before diving into the conversion of 2/25, let's briefly review the concepts of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 2/25, 2 represents the number of parts we have, and 25 represents the total number of equal parts the whole is divided into.
A percentage is a way of expressing a fraction or decimal as a proportion of 100. The word "percent" literally means "per hundred," indicating the number of parts out of 100. Percentages are widely used because they provide a standardized way to compare and understand proportions. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 2/25 to a Percentage: The Step-by-Step Process
There are several ways to convert the fraction 2/25 into a percentage. Here are two common methods:
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This method involves two steps: first, converting the fraction to a decimal, and then converting the decimal to a percentage.
-
Convert the fraction to a decimal: To convert a fraction to a decimal, we divide the numerator by the denominator. In this case, we divide 2 by 25:
2 ÷ 25 = 0.08
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent sign (%).
0.08 × 100 = 8%
Therefore, 2/25 is equal to 8%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. Since percentages are based on 100, this directly gives us the percentage.
-
Determine the multiplication factor: We need to find a number that, when multiplied by the denominator (25), results in 100. This number is 4 (25 x 4 = 100).
-
Multiply both the numerator and the denominator by the factor: To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by the same factor.
(2 × 4) / (25 × 4) = 8/100
-
Express as a percentage: Since the denominator is now 100, the numerator directly represents the percentage.
8/100 = 8%
Therefore, using this method also confirms that 2/25 is equal to 8%.
Mathematical Explanation: Proportions and Ratios
The conversion from a fraction to a percentage fundamentally relies on the concept of proportions and ratios. A ratio is a comparison of two quantities, while a proportion states that two ratios are equal.
In the context of 2/25, the ratio is 2:25. Converting this to a percentage involves finding an equivalent ratio where the second term (the denominator) is 100. This is achieved through the proportional equation:
2/25 = x/100
Solving for 'x' (using cross-multiplication), we get:
25x = 200 x = 200/25 x = 8
This confirms that 2/25 is equivalent to 8/100, or 8%.
Practical Applications of Percentage Conversions
Understanding percentage conversions is crucial in various real-world scenarios:
-
Financial Calculations: Calculating interest rates, discounts, taxes, and profit margins all involve percentage conversions. For example, a 8% discount on a $100 item means a reduction of $8.
-
Statistical Analysis: Percentages are essential for interpreting data and presenting findings in a clear and concise manner. For instance, understanding that 8% of a population holds a certain characteristic provides valuable insight.
-
Everyday Life: We encounter percentages regularly when calculating tips, understanding sales, or interpreting nutritional information on food labels.
-
Science and Engineering: Percentages are used extensively in various scientific and engineering fields to express proportions, concentrations, and errors.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, you can convert any fraction to a percentage using the methods described above.
Q2: What if the decimal representation of the fraction is recurring (e.g., 1/3)?
A2: You can still express the fraction as a percentage, but the percentage will be an approximation if the decimal has repeating digits. For example, 1/3 ≈ 33.33%.
Q3: Is there a quicker way to calculate percentages in my head?
A3: For some common fractions, memorizing their percentage equivalents can be helpful. For other calculations, using simple mental arithmetic techniques can aid speed and accuracy. For example, finding 10% of a number is the same as dividing by 10.
Conclusion
Converting 2/25 to a percentage, resulting in 8%, demonstrates a fundamental mathematical skill with far-reaching applications. Mastering this conversion method provides a solid foundation for understanding and applying percentages in various aspects of life, from personal finance to scientific analysis. The methods outlined above, coupled with an understanding of the underlying mathematical principles of proportions and ratios, empower you to confidently tackle similar fraction-to-percentage conversions with ease and accuracy. Remember to practice regularly to solidify your understanding and build confidence in your mathematical skills. Understanding percentages is not just about solving problems; it's about developing a critical thinking skill that enables you to interpret and analyze information effectively in the real world.
Latest Posts
Latest Posts
-
Words Ending In One Z
Sep 15, 2025
-
Comparison With Or Comparison To
Sep 15, 2025
-
Contact Solution With Boric Acid
Sep 15, 2025
-
Two Letter Words Containing V
Sep 15, 2025
-
Partial Fraction Of Repeated Roots
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 2 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.