2 4 As A Decimal
elan
Sep 18, 2025 · 6 min read
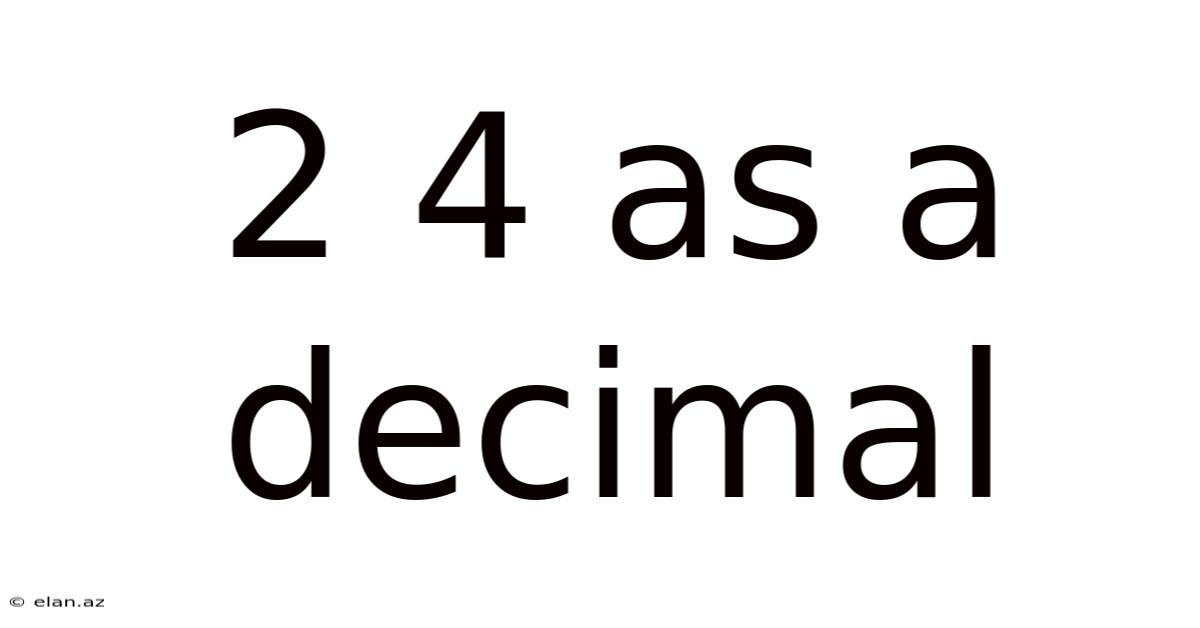
Table of Contents
Understanding 2/4 as a Decimal: A Comprehensive Guide
The seemingly simple fraction 2/4 often serves as a foundational stepping stone in understanding decimals. This article will delve deep into converting 2/4 to its decimal equivalent, exploring the underlying mathematical principles and providing a comprehensive understanding for learners of all levels. We'll cover various methods for conversion, address common misconceptions, and explore the broader implications of this seemingly basic concept. By the end, you'll not only know the decimal value of 2/4 but also possess a robust understanding of fraction-to-decimal conversion.
Introduction to Fractions and Decimals
Before diving into the conversion of 2/4, let's briefly review the fundamental concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 2/4, 2 is the numerator and 4 is the denominator. This means we have 2 parts out of a total of 4 equal parts.
A decimal, on the other hand, represents a number based on powers of 10. The decimal point separates the whole number part from the fractional part. For instance, 0.5 represents five-tenths (5/10), and 0.25 represents twenty-five hundredths (25/100). Understanding the relationship between fractions and decimals is crucial for various mathematical operations.
Method 1: Simplifying the Fraction
The simplest and most intuitive method to convert 2/4 to a decimal involves simplifying the fraction first. Notice that both the numerator (2) and the denominator (4) are divisible by 2. Simplifying the fraction means finding an equivalent fraction with smaller numbers.
Dividing both the numerator and the denominator by 2, we get:
2 ÷ 2 / 4 ÷ 2 = 1/2
Now, we have a much simpler fraction, 1/2. This is a common fraction, and its decimal equivalent is readily known to many: 0.5. Therefore, 2/4 simplified to 1/2 is equal to 0.5 as a decimal.
Method 2: Long Division
Another method for converting a fraction to a decimal involves using long division. This method is particularly useful when dealing with fractions that are not easily simplified. To convert 2/4 to a decimal using long division, we divide the numerator (2) by the denominator (4):
0.5
4 | 2.0
-2.0
0
We add a decimal point and a zero to the numerator (2) to facilitate the division. 4 goes into 2 zero times, so we place a zero above the decimal point. Then, 4 goes into 20 five times (4 x 5 = 20). The remainder is 0, indicating that the division is complete. Therefore, the decimal equivalent of 2/4 is 0.5.
Method 3: Using Equivalent Fractions with a Denominator of 10, 100, etc.
This method involves finding an equivalent fraction where the denominator is a power of 10 (10, 100, 1000, etc.). This is because decimals are based on powers of 10. In the case of 2/4, we already simplified it to 1/2. To express 1/2 as a decimal using this method, we need to find an equivalent fraction with a denominator of 10:
To change the denominator from 2 to 10, we multiply it by 5. To maintain the equivalence, we must also multiply the numerator by 5:
(1 x 5) / (2 x 5) = 5/10
Now, 5/10 can be easily written as a decimal: 0.5.
Understanding the Concept of Equivalence
It's crucial to understand that simplifying a fraction doesn't change its value; it only represents it in a simpler form. The fractions 2/4 and 1/2 are equivalent; they represent the same amount. Similarly, the fraction 5/10 and 1/2 are also equivalent, and all three represent the same decimal value: 0.5. This concept of equivalence is fundamental in understanding fractions and their decimal representations.
Applying the Concept: Real-World Examples
The conversion of fractions to decimals is not just an abstract mathematical exercise; it has numerous real-world applications. Consider these examples:
-
Calculating percentages: Percentages are essentially fractions with a denominator of 100. Converting a fraction to a decimal makes it easier to calculate percentages. For instance, if you scored 2 out of 4 points on a quiz (2/4), that's equivalent to 0.5 or 50%.
-
Measuring quantities: Many measurements involve decimals. If a recipe calls for 1/2 a cup of flour, it's equivalent to 0.5 cups, which can be easily measured using a measuring cup with decimal markings.
-
Financial calculations: In finance, decimals are commonly used to represent amounts of money. Converting fractions to decimals simplifies financial calculations, such as calculating interest rates or discounts.
-
Data analysis: In data analysis and statistics, decimals are frequently used to represent proportions and probabilities. Converting fractions to decimals simplifies data representation and analysis.
Frequently Asked Questions (FAQs)
Q: Why is it important to simplify fractions before converting them to decimals?
A: Simplifying fractions makes the conversion process easier and less prone to errors. Working with smaller numbers simplifies the long division process and reduces the risk of calculation mistakes.
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that are not factors of powers of 10 (i.e., not divisible by only 2 and/or 5) will result in repeating or non-terminating decimals. For example, 1/3 results in the repeating decimal 0.333...
Q: What if I get a remainder in the long division method?
A: If you have a remainder after long division, it means the decimal is either repeating or non-terminating. You can continue the division to a certain number of decimal places for practical purposes.
Q: Are there other methods to convert fractions to decimals?
A: Yes, calculators are a common and efficient way to convert fractions to decimals. More advanced mathematical techniques also exist, but they are typically used for more complex fractions.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting 2/4 to its decimal equivalent (0.5) is a fundamental skill in mathematics. This seemingly simple conversion process underlies many more complex mathematical concepts. By understanding the different methods for conversion – simplification, long division, and using equivalent fractions – and appreciating the concept of equivalence, you build a solid foundation for more advanced mathematical studies and real-world applications. Mastering this skill not only improves your mathematical prowess but also enhances your problem-solving capabilities across various disciplines. Remember, practice is key to mastering this skill, so work through various examples to reinforce your understanding and build confidence.
Latest Posts
Latest Posts
-
Inequality In A Number Line
Sep 18, 2025
-
Meaning Of The Name Fox
Sep 18, 2025
-
1 3 Multiplied By 2
Sep 18, 2025
-
Bad Words Beginning With M
Sep 18, 2025
-
Accrued Income Vs Deferred Income
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2 4 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.