2 X 2 X 12
elan
Sep 23, 2025 · 6 min read
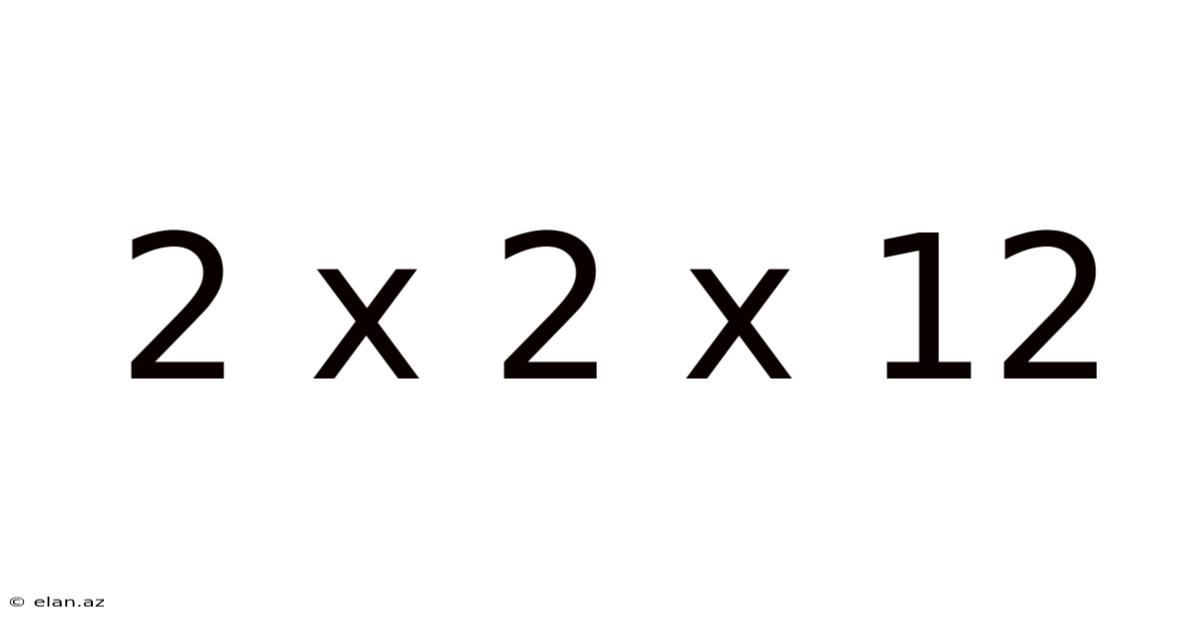
Table of Contents
Decomposing 2 x 2 x 12: A Deep Dive into Multiplication, Factors, and Volume
This article explores the seemingly simple mathematical expression "2 x 2 x 12," delving far beyond the basic arithmetic answer of 48. We'll uncover the underlying principles of multiplication, examine the factors involved, explore its geometrical representation, and connect it to real-world applications. This exploration will be suitable for learners of all levels, from those grasping the basics of multiplication to those seeking a deeper understanding of mathematical concepts.
Introduction: Beyond the Obvious Calculation
At first glance, 2 x 2 x 12 appears straightforward. A quick calculation yields the answer 48. However, this seemingly simple equation offers a rich opportunity to explore several fundamental mathematical concepts. This exploration extends beyond simply finding the product; we'll delve into the factors, explore the concept of volume, and investigate the various ways this calculation can be represented and applied. We'll also touch upon the commutative and associative properties of multiplication.
Understanding the Factors: Building Blocks of Multiplication
The expression 2 x 2 x 12 involves three factors: 2, 2, and 12. A factor is a number that divides another number without leaving a remainder. Understanding factors is crucial to grasping the concept of multiplication. In this instance:
- 2: Is a prime number, meaning it's only divisible by 1 and itself. It appears twice in the expression, highlighting the concept of repeated multiplication.
- 12: Is a composite number, meaning it has more than two factors (1, 2, 3, 4, 6, and 12). This factor introduces more complexity and opportunities for further analysis. We can break down 12 into its prime factorization: 2 x 2 x 3.
This prime factorization of 12 is particularly insightful. Substituting the prime factorization into the original equation, we get: 2 x 2 x (2 x 2 x 3) = 2 x 2 x 2 x 2 x 3 = 48. This demonstrates that any number can be represented by its prime factors, providing a foundational understanding of number theory.
The Commutative and Associative Properties: Rearranging the Equation
Multiplication possesses two crucial properties that allow us to rearrange the factors without altering the product:
-
Commutative Property: The order of the factors doesn't affect the product. This means 2 x 2 x 12 = 2 x 12 x 2 = 12 x 2 x 2 = 48. This property is essential for simplifying calculations and solving more complex equations.
-
Associative Property: The grouping of factors doesn't affect the product. This means (2 x 2) x 12 = 2 x (2 x 12) = 4 x 12 = 2 x 24 = 48. This property aids in streamlining calculations, particularly with more significant numbers.
By understanding and applying these properties, we can manipulate the equation to make calculations more efficient.
Geometrical Representation: Volume of a Rectangular Prism
The expression 2 x 2 x 12 has a strong geometrical interpretation. It represents the volume of a rectangular prism (or cuboid). Imagine a box with:
- Length: 12 units
- Width: 2 units
- Height: 2 units
The volume of this box is calculated by multiplying the length, width, and height: 12 x 2 x 2 = 48 cubic units. This connection between arithmetic and geometry is fundamental in mathematics and has numerous practical applications in fields like engineering, architecture, and physics. Visualizing the equation in this way provides a concrete understanding of what the calculation represents. You could imagine this as a box of chocolates, a storage container, or even a building block.
Real-World Applications: Beyond Abstract Concepts
The calculation 2 x 2 x 12, while seemingly abstract, finds its place in various real-world situations:
-
Packaging and Shipping: Companies use these calculations to determine the volume of packaging needed for products. Knowing the dimensions of the product allows them to optimize packaging size and minimize shipping costs.
-
Construction and Engineering: Architects and engineers use these calculations to determine the volume of materials needed for construction projects. This is critical for accurate cost estimations and project planning.
-
Data Storage: In computer science, storage capacity is often expressed in terms of volume (e.g., gigabytes). Understanding multiplication helps in calculating total storage capacity.
-
Everyday Scenarios: Consider arranging items in a grid. If you have 12 rows, each containing 2 x 2 items, then you have a total of 48 items.
Further Exploration: Factors, Multiples, and Prime Factorization
We've already touched upon factors and prime factorization. Let's expand this understanding further:
-
Factors of 48: Beyond the factors 2, 2, and 12, we can identify all factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. This demonstrates the various ways 48 can be decomposed into smaller multiplicative components.
-
Multiples of 48: Multiples of 48 are numbers that are divisible by 48 without a remainder. Some examples are 48, 96, 144, 192, etc. Understanding multiples is important in many mathematical contexts, including finding least common multiples and greatest common divisors.
-
Prime Factorization of 48: As we've seen, the prime factorization of 48 is 2 x 2 x 2 x 2 x 3 (or 2<sup>4</sup> x 3). This factorization is unique to 48 and is fundamental to many number theory concepts.
Advanced Concepts: Exponents and Powers
The repeated multiplication of 2 in the expression 2 x 2 x 12 can be simplified using exponents. We can rewrite 2 x 2 as 2², meaning 2 raised to the power of 2. Thus, the expression becomes 2² x 12 = 4 x 12 = 48. This introduces the concept of exponents, a powerful tool for representing repeated multiplication and simplifying complex calculations. Understanding exponents is crucial for higher-level mathematics, including algebra, calculus, and beyond.
Frequently Asked Questions (FAQ)
-
Q: What is the only even prime number? A: The only even prime number is 2.
-
Q: What is the difference between a factor and a multiple? A: A factor divides a number without a remainder, while a multiple is a number that is the product of a given number and an integer.
-
Q: How do I find the prime factorization of a number? A: Start by dividing the number by the smallest prime number (2). Continue dividing by prime numbers until you reach 1. The prime numbers you used are the prime factorization.
-
Q: What are the practical uses of understanding 2 x 2 x 12? A: It has applications in calculating volumes, areas, optimizing packaging, and many other real-world scenarios, particularly those involving spatial measurements and organization.
-
Q: Can I use a calculator for this? A: Yes, a basic calculator will provide the answer quickly (48). However, this exercise emphasizes understanding the underlying mathematical concepts, which a calculator alone cannot teach.
Conclusion: A Comprehensive Look at a Simple Equation
While the calculation 2 x 2 x 12 may seem trivial at first glance, its exploration reveals a wealth of mathematical principles. We've delved into the concepts of factors, multiples, prime factorization, the commutative and associative properties of multiplication, and the geometrical representation of volume. The ability to understand and apply these concepts is crucial for success in mathematics and its numerous real-world applications. This exercise illustrates how seemingly simple equations can offer a deep dive into fundamental mathematical principles. The exploration extends beyond the simple answer of 48, opening the door to a broader understanding of numbers, their relationships, and their impact on our world. Remember, even in the simplest calculations, profound mathematical concepts lie waiting to be discovered.
Latest Posts
Latest Posts
-
Different Types Of Organisational Structures
Sep 23, 2025
-
Use Immediately In A Sentence
Sep 23, 2025
-
Best Christmas Present For Husband
Sep 23, 2025
-
Are Fish Cold Blooded Animals
Sep 23, 2025
-
8th Letter Of The Alphabet
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.