2 X 5 X 3
elan
Sep 18, 2025 · 6 min read
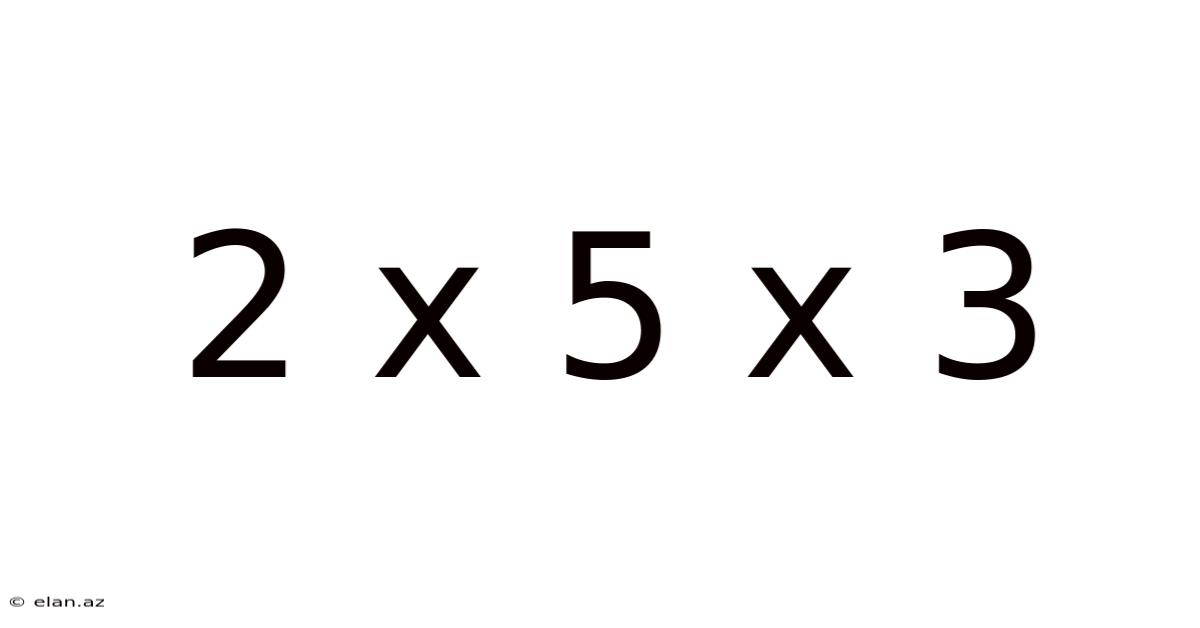
Table of Contents
Decoding 2 x 5 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "2 x 5 x 3," delving beyond the immediate answer to uncover the underlying principles of multiplication, its various applications in everyday life, and its significance in more advanced mathematical concepts. We'll explore different methods of solving this equation, discuss its real-world implications, and even touch upon its role in higher-level mathematics. This comprehensive guide is perfect for anyone looking to solidify their understanding of basic arithmetic and explore its wider context.
Introduction: Understanding the Fundamentals of Multiplication
At its core, multiplication is repeated addition. The expression "2 x 5 x 3" signifies that we are adding the number 2, five times, and then multiplying the result by 3. It's a concise way of representing a repetitive addition problem. Understanding this fundamental relationship between addition and multiplication is crucial for grasping the concept thoroughly.
We can visualize this problem in several ways. Imagine having 2 bags of apples, with each bag containing 5 apples. To find the total number of apples, we would multiply 2 (bags) by 5 (apples per bag). Then, imagine that we have 3 such sets of bags and apples. To get the grand total, we multiply the initial result by 3. This simple example showcases how multiplication simplifies complex counting scenarios.
Methods for Solving 2 x 5 x 3
There are several ways to approach solving "2 x 5 x 3," highlighting the commutative and associative properties of multiplication.
-
Method 1: Sequential Multiplication: This involves solving the equation step-by-step, from left to right. First, we calculate 2 x 5 = 10. Then, we multiply the result by 3: 10 x 3 = 30. This is a straightforward and commonly used method.
-
Method 2: Commutative Property: The commutative property of multiplication states that the order of numbers does not affect the product. Therefore, we can rearrange the numbers in any order: 5 x 2 x 3, 3 x 2 x 5, and so on. This flexibility allows us to choose an order that simplifies the calculation. For example, 2 x 3 = 6, then 6 x 5 = 30.
-
Method 3: Associative Property: The associative property states that the grouping of numbers does not affect the product. We can group the numbers in different ways: (2 x 5) x 3 or 2 x (5 x 3). This allows for a strategic approach, potentially simplifying calculations. For instance, 5 x 3 = 15, and then 2 x 15 = 30.
All three methods lead to the same answer: 30. The choice of method depends on personal preference and the specific context of the problem. However, understanding these properties is vital for more complex calculations and algebraic manipulations.
Real-World Applications: Beyond the Classroom
The seemingly simple equation "2 x 5 x 3" has numerous applications in everyday life, often without us even realizing it:
-
Shopping: Imagine buying 2 packs of cookies, with each pack containing 5 cookies, and you need 3 such sets for a party. The total number of cookies needed is 2 x 5 x 3 = 30 cookies.
-
Construction: A builder needs to lay 2 rows of bricks, each row consisting of 5 bricks, and they need to repeat this pattern across 3 sections of a wall. The total number of bricks required would be 2 x 5 x 3 = 30 bricks.
-
Cooking: A recipe calls for 2 tablespoons of flour for each batch of cookies, and you need to make 5 batches. If you need to triple the recipe, the total amount of flour would be 2 x 5 x 3 = 30 tablespoons.
-
Gardening: You plant 2 rows of flowers, each row containing 5 plants, and you need to plant 3 such flower beds. You'll need a total of 2 x 5 x 3 = 30 plants.
These examples highlight how multiplication, even in its simplest form, is integral to our daily routines, helping us efficiently calculate quantities and solve everyday problems.
Expanding the Concept: Multiplication in Advanced Mathematics
While "2 x 5 x 3" represents basic arithmetic, the underlying principles extend to far more complex mathematical concepts:
-
Algebra: The concept of multiplication is fundamental to algebraic expressions and equations. Variables can be multiplied just like numbers, allowing us to represent and solve problems involving unknown quantities. For example, 2x * 5y * 3z = 30xyz.
-
Calculus: Multiplication plays a critical role in differentiation and integration, two core concepts in calculus. Derivatives and integrals often involve multiplying functions and their components.
-
Linear Algebra: Matrices are rectangular arrays of numbers, and matrix multiplication is a fundamental operation in linear algebra, used extensively in computer graphics, data analysis, and other fields.
-
Number Theory: The concept of prime factorization, where numbers are broken down into their prime factors (e.g., 30 = 2 x 3 x 5), is central to number theory, a branch of mathematics that deals with the properties of integers. The expression 2 x 5 x 3 is a prime factorization of 30.
This demonstrates how a simple concept like "2 x 5 x 3" forms the foundation of more advanced mathematical principles and applications.
Exploring Factors and Multiples
The expression 2 x 5 x 3 introduces the concepts of factors and multiples.
-
Factors: The numbers 2, 3, and 5 are factors of 30 because they divide 30 evenly without leaving a remainder. Finding factors is crucial in simplifying fractions and solving equations.
-
Multiples: 30 is a multiple of 2, 3, 5, 6, 10, and 15 because it can be obtained by multiplying each of these numbers by an integer. Understanding multiples helps in determining common denominators and solving problems involving proportions.
The interplay between factors and multiples is critical in numerous mathematical applications.
Frequently Asked Questions (FAQs)
-
What is the answer to 2 x 5 x 3? The answer is 30.
-
Can I solve this equation using a calculator? Yes, you can simply enter "2 * 5 * 3" into any calculator to get the answer 30.
-
What are the different ways to write this multiplication problem? You can write it as 2 x 5 x 3, (2 x 5) x 3, 2 x (5 x 3), 5 x 2 x 3, etc. The order and grouping don't change the result.
-
Why is understanding multiplication important? Multiplication is fundamental for everyday calculations, from shopping to construction, and it forms the basis of more advanced mathematical concepts.
-
How can I practice my multiplication skills? Practice regularly using flashcards, worksheets, or interactive online games. Focus on understanding the underlying concepts rather than just memorizing multiplication tables.
Conclusion: The Enduring Significance of a Simple Equation
While the equation "2 x 5 x 3" appears simple, its significance extends far beyond the immediate answer of 30. It embodies fundamental mathematical principles, provides a foundation for more advanced concepts, and finds practical applications in numerous real-world scenarios. Understanding this seemingly simple equation provides a robust base for tackling more intricate mathematical problems and develops crucial problem-solving skills applicable across various disciplines. By mastering the principles behind this simple multiplication, we unlock a deeper appreciation for the power and versatility of mathematics in our lives. It’s not just about getting the answer; it's about understanding the 'why' behind the answer, which empowers us to tackle even more complex challenges in the future.
Latest Posts
Latest Posts
-
What Are Client Server Networks
Sep 19, 2025
-
171cm In Ft And Inches
Sep 19, 2025
-
Volume Of Cubes And Cuboids
Sep 19, 2025
-
My Mother Taught Me Song
Sep 19, 2025
-
Fruit That Begins With H
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2 X 5 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.