20 Percent As A Fraction
elan
Sep 12, 2025 · 6 min read
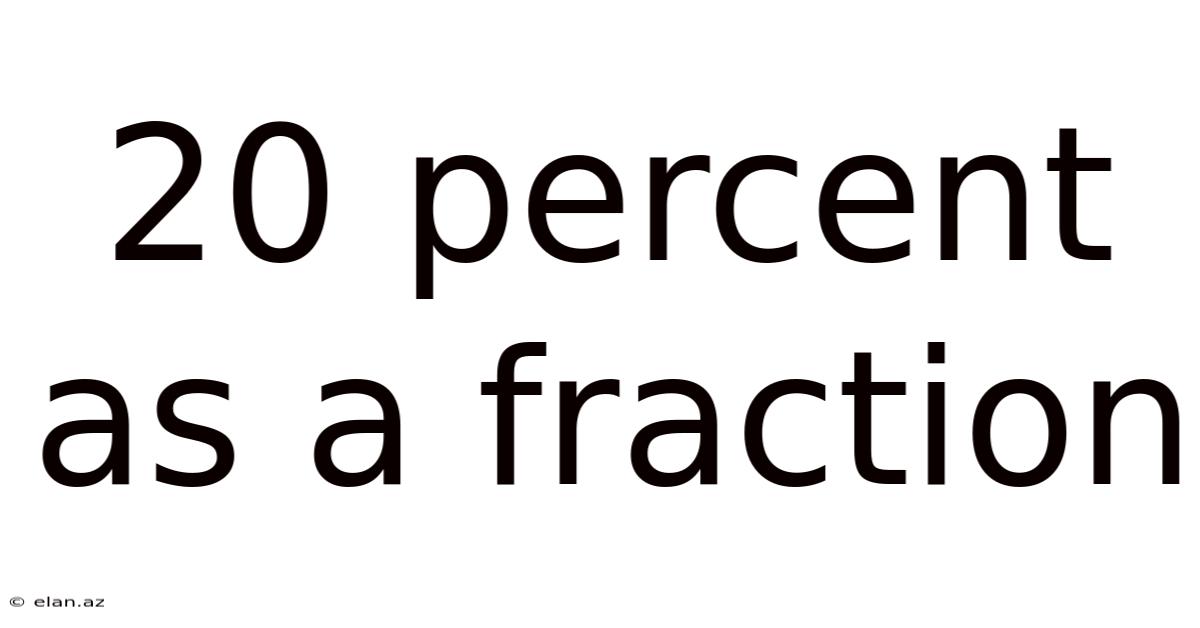
Table of Contents
20 Percent as a Fraction: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics, crucial for everyday life and various professional fields. This comprehensive guide delves into the concept of 20 percent, explaining its representation as a fraction, simplifying it to its lowest terms, and exploring its applications in different contexts. We'll cover everything from the basic conversion process to more advanced applications, ensuring a thorough understanding for learners of all levels. This article will equip you with the knowledge to confidently handle percentage calculations involving 20 percent in fractions and decimals.
Understanding Percentages and Fractions
Before diving into the specifics of 20 percent, let's establish a solid foundation. A percentage represents a fraction of 100. The word "percent" itself originates from the Latin phrase "per centum," meaning "out of one hundred." Therefore, 20 percent literally means 20 out of 100.
Fractions, on the other hand, express parts of a whole. They are represented by a numerator (the top number) and a denominator (the bottom number), separated by a line. The denominator indicates the total number of parts, while the numerator indicates the number of parts being considered.
Converting 20 Percent to a Fraction
Converting a percentage to a fraction is a straightforward process. Here's how to convert 20 percent to a fraction:
-
Write the percentage as a fraction with a denominator of 100. Since percent means "per hundred," 20 percent can be written as 20/100.
-
Simplify the fraction. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. The GCD of 20 and 100 is 20. Dividing both the numerator and the denominator by 20, we get:
20/100 = (20 ÷ 20) / (100 ÷ 20) = 1/5
Therefore, 20 percent as a fraction is 1/5.
Different Representations of 20 Percent
While 1/5 is the simplest form, 20 percent can be represented by other equivalent fractions. Any fraction that simplifies to 1/5 is equal to 20 percent. For example:
- 2/10: This fraction simplifies to 1/5 when both the numerator and denominator are divided by 2.
- 4/20: This fraction simplifies to 1/5 when both the numerator and denominator are divided by 4.
- 10/50: This fraction simplifies to 1/5 when both the numerator and denominator are divided by 10.
These equivalent fractions all represent the same proportion: 20 percent or 1/5.
Applications of 20 Percent as a Fraction (1/5)
The fraction 1/5, representing 20 percent, has numerous practical applications across various fields:
-
Calculating Discounts: If a store offers a 20 percent discount, you can easily calculate the discount amount by multiplying the original price by 1/5. For instance, a $100 item with a 20 percent discount would be reduced by $100 x (1/5) = $20.
-
Determining Portions: Imagine dividing a pizza into 5 equal slices. One slice represents 1/5 or 20 percent of the whole pizza.
-
Financial Calculations: Interest rates, profit margins, and tax calculations often involve percentages. Understanding how to convert percentages to fractions simplifies these calculations. For example, calculating 20% interest on a $5000 loan is equivalent to calculating (1/5) * $5000 = $1000.
-
Data Analysis: In statistics and data analysis, percentages are frequently used to represent proportions within a dataset. Converting these percentages to fractions can help in simplifying calculations and interpreting the data more efficiently.
Working with 20 Percent in Decimal Form
While fractions are useful for understanding proportions, decimals are often more practical for calculations, especially when using calculators or computers. To convert 20 percent to a decimal, simply divide the percentage by 100:
20% ÷ 100 = 0.20 or 0.2
Converting Decimals Back to Fractions
It's important to be able to convert decimals back to fractions as well. To convert 0.2 to a fraction, follow these steps:
-
Write the decimal as a fraction with a denominator of 1. 0.2 can be written as 0.2/1.
-
Multiply both the numerator and denominator by a power of 10 to eliminate the decimal point. In this case, multiplying by 10 will remove the decimal: (0.2 x 10) / (1 x 10) = 2/10.
-
Simplify the fraction. 2/10 simplifies to 1/5 by dividing both numerator and denominator by their GCD, which is 2.
This demonstrates the equivalence between 0.2, 20%, and 1/5.
Advanced Applications: Proportions and Ratios
Understanding 20 percent as a fraction (1/5) is key to solving proportion and ratio problems. For example:
-
Problem: A recipe calls for 20 percent of the ingredients to be sugar. If the total weight of ingredients is 500 grams, how many grams of sugar are needed?
-
Solution: 20 percent is equivalent to 1/5. Therefore, the amount of sugar needed is (1/5) * 500 grams = 100 grams.
This example illustrates how easily we can apply the fraction representation of 20 percent to solve real-world problems.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand and work with. It presents the proportion in its most concise and efficient form. For example, 20/100 is less intuitive than 1/5.
Q2: Can I use a calculator to convert percentages to fractions?
A2: While you can't directly convert percentages to fractions using most basic calculators, you can use it to find the decimal equivalent (20%/100 = 0.2) and then convert that decimal to a fraction manually or using a fraction calculator.
Q3: What if I have a percentage that doesn't easily simplify to a whole number fraction?
A3: Some percentages will result in fractions with larger numbers. For instance, 23% is 23/100 and does not simplify further. In these cases, the fraction is still a valid representation.
Q4: How does understanding 20% as a fraction help in real-world situations?
A4: It allows for quick mental calculations, especially in scenarios involving estimations and approximations. For instance, quickly determining a 20% tip at a restaurant becomes much easier with the understanding of 1/5.
Q5: Are there any online tools to help with percentage-to-fraction conversions?
A5: Yes, many online calculators and converters can perform this conversion. However, understanding the underlying mathematical principles is crucial for developing a solid grasp of the concept.
Conclusion
Understanding 20 percent as a fraction, specifically its simplified form 1/5, is a valuable mathematical skill. This comprehensive guide has explored the conversion process, demonstrated its practical applications in diverse scenarios, and addressed frequently asked questions. By mastering this concept, you'll gain confidence in handling percentage calculations and enhance your problem-solving abilities in various contexts. Remember that the ability to easily switch between percentages, fractions, and decimals is essential for success in mathematics and its various applications in the real world. Continue practicing these conversions to solidify your understanding and become proficient in working with percentages and fractions.
Latest Posts
Latest Posts
-
10 Algebra Questions And Answers
Sep 12, 2025
-
180 Sq Meters In Feet
Sep 12, 2025
-
What Percent Is 2 Thirds
Sep 12, 2025
-
Melting Point And Boiling Point
Sep 12, 2025
-
Will Be Send Or Sent
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.