28 40 As A Percentage
elan
Sep 16, 2025 · 5 min read
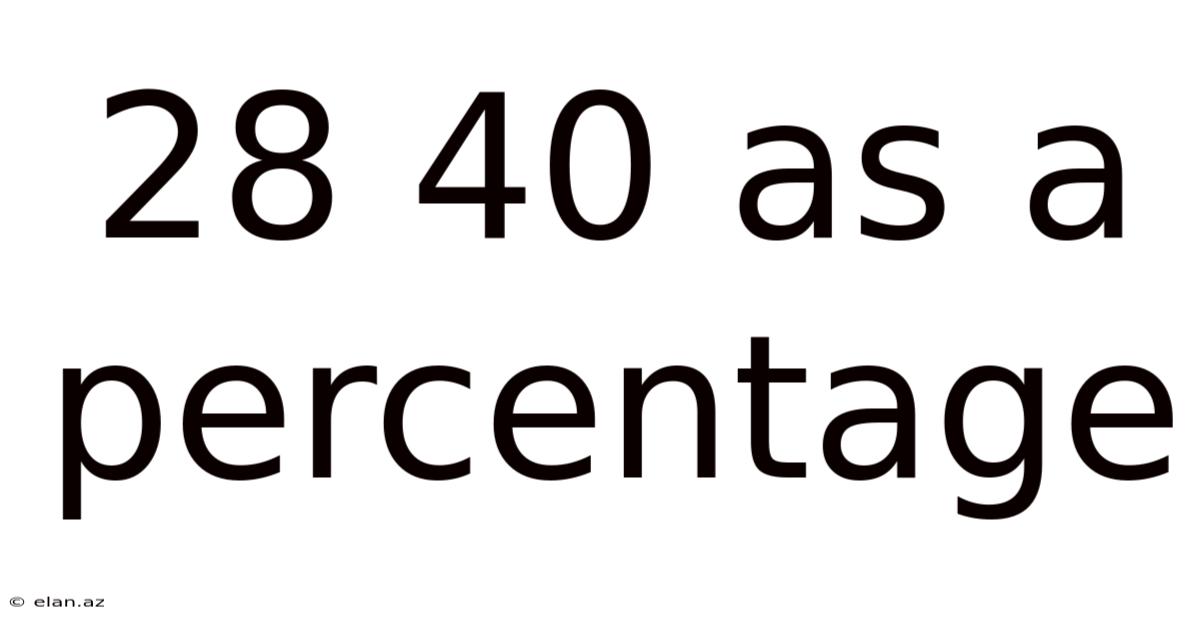
Table of Contents
Decoding 28 out of 40: A Comprehensive Guide to Percentage Calculations and Their Applications
Understanding percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial planning and everyday life. This article delves into the calculation of 28 out of 40 as a percentage, providing a step-by-step guide, exploring different calculation methods, and demonstrating the broader implications of percentage calculations. We will also address common misconceptions and answer frequently asked questions to ensure a thorough understanding of this crucial mathematical concept.
Understanding the Basics: What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The symbol % represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are useful for comparing proportions, showing changes over time, or representing parts of a whole.
Calculating 28 out of 40 as a Percentage: Step-by-Step Guide
The fundamental method for calculating a percentage involves these three simple steps:
-
Form a Fraction: Express the given numbers as a fraction. In this case, it's 28/40. This fraction represents the proportion of 28 out of a total of 40.
-
Convert the Fraction to a Decimal: Divide the numerator (28) by the denominator (40). 28 ÷ 40 = 0.7
-
Convert the Decimal to a Percentage: Multiply the decimal by 100. 0.7 x 100 = 70
Therefore, 28 out of 40 is 70%.
Alternative Calculation Methods
While the above method is the most straightforward, alternative approaches can be equally effective, especially for those comfortable with mental math or using calculators.
-
Simplifying the Fraction: Before converting to a decimal, you can simplify the fraction 28/40 by finding the greatest common divisor (GCD) of 28 and 40, which is 4. Dividing both the numerator and the denominator by 4 gives us 7/10. This simplifies the conversion to a decimal and percentage, as 7/10 = 0.7, and 0.7 x 100 = 70%.
-
Using Proportions: Set up a proportion:
28/40 = x/100. Cross-multiply and solve for x:40x = 2800. Divide both sides by 40:x = 70. Therefore, x represents 70%. -
Using a Calculator: Most calculators have a percentage function. Simply input 28 ÷ 40 and then multiply by 100. The calculator will directly provide the answer: 70%.
Understanding the Context: Applications of Percentage Calculations
The application of percentage calculations extends far beyond simple mathematical problems. Here are some real-world examples:
-
Academic Performance: If a student scores 28 out of 40 on a test, their score is 70%. This allows for easy comparison of performance across different tests or students.
-
Financial Analysis: Businesses use percentages to track various metrics like profit margins, revenue growth, and expense ratios. For example, a 70% profit margin signifies that 70% of revenue is profit.
-
Data Representation: Percentages are crucial for visually representing data in charts and graphs, making it easier to understand complex information at a glance. Pie charts and bar graphs frequently utilize percentages to illustrate proportions.
-
Discount Calculations: Sales and discounts are often expressed as percentages. A 70% discount means the price is reduced by 70% of the original price.
-
Interest Rates: Interest rates on loans and investments are expressed as percentages. A 7% interest rate means that for every 100 units invested, you'll earn 7 units in interest.
-
Tax Calculations: Taxes are often calculated as a percentage of income or the value of goods and services.
Common Misconceptions about Percentage Calculations
Several common misconceptions can lead to errors in percentage calculations:
-
Confusing Percentage with Decimal: Remember that a percentage is a fraction out of 100, while a decimal represents a fraction. You need to convert between them using the appropriate multiplication or division.
-
Incorrectly Calculating Percentage Increase/Decrease: Calculating percentage change requires careful consideration of the original value. Percentage increase is calculated as [(New Value - Old Value) / Old Value] x 100, while percentage decrease is calculated as [(Old Value - New Value) / Old Value] x 100.
-
Ignoring Significant Figures: In scientific and engineering contexts, paying attention to significant figures is crucial for maintaining accuracy.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage of a number?
- A: To find the percentage of a number, convert the percentage to a decimal by dividing by 100, then multiply the decimal by the number. For example, to find 70% of 200, calculate 0.7 x 200 = 140.
-
Q: How do I express a fraction as a percentage?
- A: Divide the numerator by the denominator to get a decimal, then multiply the decimal by 100 and add the % symbol.
-
Q: What if the number is larger than 100%?
- A: Percentages can exceed 100%. This indicates that the value is more than the reference value (the whole). For example, a 120% increase means the value has increased by 20% more than the original value.
-
Q: How can I improve my percentage calculation skills?
- A: Practice is key. Work through various problems, starting with simple ones and gradually increasing the complexity. Use different methods to build a solid understanding. You can also find numerous online resources and practice exercises.
Conclusion
Calculating 28 out of 40 as a percentage (70%) is a simple yet fundamental process with wide-ranging applications. Mastering percentage calculations is vital for success in many academic, professional, and personal situations. By understanding the underlying principles and common pitfalls, you can confidently tackle percentage problems and use them effectively to analyze data, make informed decisions, and better comprehend the world around you. Remember to practice regularly, and don't hesitate to utilize different methods to find the one that best suits your learning style. The more you practice, the more intuitive percentage calculations will become.
Latest Posts
Latest Posts
-
Simple Heart Diagram With Labels
Sep 16, 2025
-
1 100 In Decimal Form
Sep 16, 2025
-
Where Are Magnetic Fields Strongest
Sep 16, 2025
-
Animal That Starts With M
Sep 16, 2025
-
Words Using The Prefix Sub
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 28 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.