29 35 As A Percentage
elan
Sep 15, 2025 · 5 min read
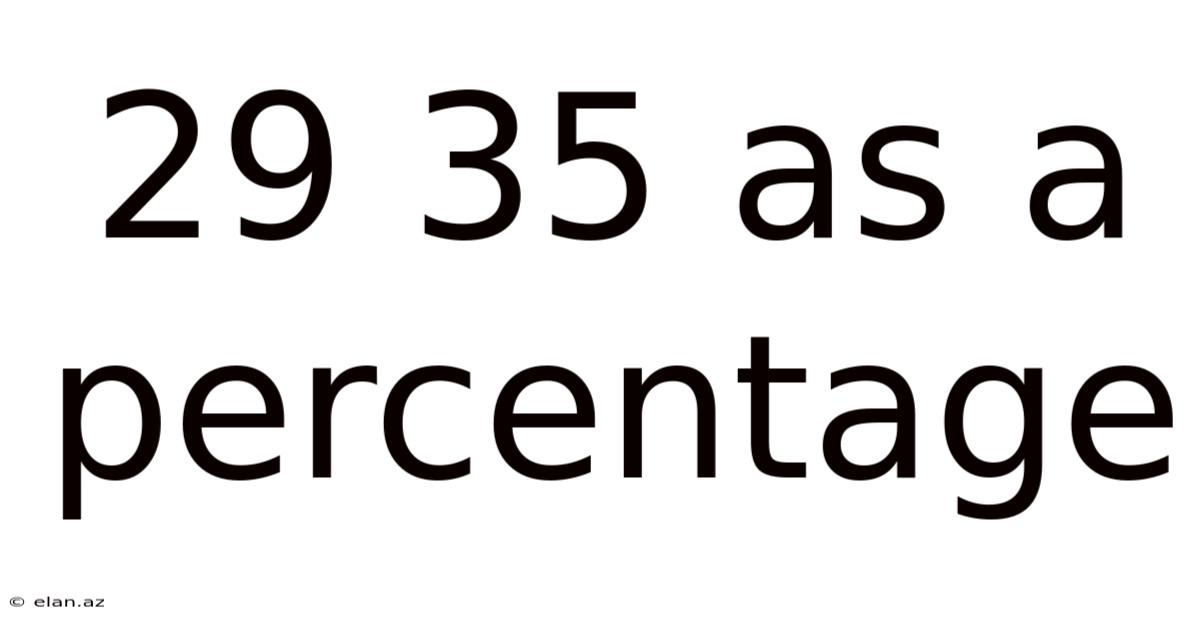
Table of Contents
29 out of 35 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to advanced statistical analysis. Understanding how to express one number as a percentage of another is crucial for interpreting data and making informed decisions. This article will comprehensively explain how to calculate 29 out of 35 as a percentage, delve into the underlying mathematical principles, explore different methods of calculation, and offer practical examples to solidify your understanding. We'll also address common misconceptions and answer frequently asked questions. This guide ensures you not only get the answer but also gain a deeper appreciation of percentage calculations.
Understanding Percentages
A percentage is simply a fraction expressed as a portion of 100. The symbol "%" represents "per cent," meaning "out of one hundred." To express a fraction as a percentage, we need to find its equivalent fraction with a denominator of 100. For example, 1/2 is equivalent to 50/100, or 50%. This concept is central to understanding how to calculate 29 out of 35 as a percentage.
Calculating 29 out of 35 as a Percentage: The Step-by-Step Guide
There are several ways to calculate 29 out of 35 as a percentage. Let's explore the most common methods:
Method 1: Using the Fraction Method
-
Express the numbers as a fraction: The problem "29 out of 35" can be represented as the fraction 29/35.
-
Convert the fraction to a decimal: To convert a fraction to a decimal, divide the numerator (29) by the denominator (35). 29 ÷ 35 ≈ 0.8286
-
Convert the decimal to a percentage: Multiply the decimal by 100 to express it as a percentage. 0.8286 x 100 = 82.86%
Therefore, 29 out of 35 is approximately 82.86%.
Method 2: Using Proportions
This method utilizes the concept of proportions to solve the problem.
-
Set up a proportion: We can set up a proportion to solve for the percentage:
29/35 = x/100
-
Cross-multiply: Cross-multiply the proportion:
35x = 2900
-
Solve for x: Divide both sides by 35:
x = 2900/35 ≈ 82.86
Therefore, x ≈ 82.86%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the calculation significantly. Simply divide 29 by 35 and then multiply the result by 100. The calculator will directly provide the percentage value of approximately 82.86%.
Rounding and Accuracy
In the above calculations, we obtained the result 82.8571428571...%. This is an infinitely repeating decimal. For practical purposes, we usually round the percentage to a reasonable number of decimal places. Rounding to two decimal places, as we did earlier, gives us 82.86%. The level of rounding depends on the context; for some applications, rounding to the nearest whole number (83%) might suffice.
Practical Applications and Real-World Examples
Understanding percentage calculations is essential in various real-world scenarios:
-
Academic Performance: If a student scores 29 out of 35 on a test, their percentage score is 82.86%, providing a clear representation of their performance.
-
Sales and Marketing: Businesses use percentages to track sales figures, growth rates, and conversion rates. For example, if a company sold 29 units out of a target of 35, their sales performance can be represented as 82.86%.
-
Financial Calculations: Interest rates, discounts, and tax calculations all involve percentages.
-
Statistical Analysis: Percentages are fundamental to interpreting statistical data, expressing probabilities, and comparing different datasets.
Beyond the Calculation: Understanding the Context
While knowing that 29 out of 35 is approximately 82.86% is important, understanding the context is crucial. In an academic setting, 82.86% might represent a high grade, whereas in a sales context, it might indicate room for improvement. The interpretation of the percentage depends heavily on the situation.
Common Misconceptions about Percentages
-
Adding percentages directly: You cannot simply add percentages directly if they represent different quantities. For example, if you have a 10% increase followed by a 10% decrease, the final result is not 0%.
-
Confusing percentage change with absolute change: A percentage change describes the relative change, while an absolute change describes the raw numerical difference. Understanding both is essential for accurate interpretation.
-
Improper rounding: Incorrect rounding can lead to significant errors, especially when dealing with large numbers or sensitive calculations.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage increase or decrease?
A1: To calculate a percentage increase or decrease, find the difference between the new value and the original value, divide this difference by the original value, and then multiply by 100.
Q2: What is the difference between a percentage and a proportion?
A2: A proportion is a ratio of two numbers, while a percentage is a specific type of proportion expressed as a fraction of 100.
Q3: Can I use a spreadsheet program like Excel to calculate percentages?
A3: Yes, spreadsheet programs offer built-in functions to calculate percentages easily and efficiently. Simply use the appropriate formula, such as =29/35*100 in an Excel cell.
Q4: How do I express a percentage as a fraction or a decimal?
A4: To convert a percentage to a decimal, divide it by 100. To convert a percentage to a fraction, write it as a fraction with a denominator of 100 and then simplify.
Conclusion
Calculating 29 out of 35 as a percentage is a straightforward process, yielding a result of approximately 82.86%. Mastering this skill involves not only understanding the mathematical steps but also appreciating the context in which percentages are used and interpreting the results appropriately. This comprehensive guide provides a strong foundation for working with percentages in various real-world situations. Remember that while the calculation is relatively simple, the interpretation and application of the percentage are just as important for drawing meaningful conclusions. By understanding the underlying principles and avoiding common misconceptions, you can confidently tackle percentage calculations and apply them effectively in your daily life and professional endeavors.
Latest Posts
Latest Posts
-
Step Up Step Down Transformer
Sep 15, 2025
-
Group Of Six Crossword Clue
Sep 15, 2025
-
Toy Demonstrating Archimedes Buoyancy Principle
Sep 15, 2025
-
35 Percent As A Fraction
Sep 15, 2025
-
Malt With Cod Liver Oil
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 29 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.