29 50 As A Percentage
elan
Sep 16, 2025 · 6 min read
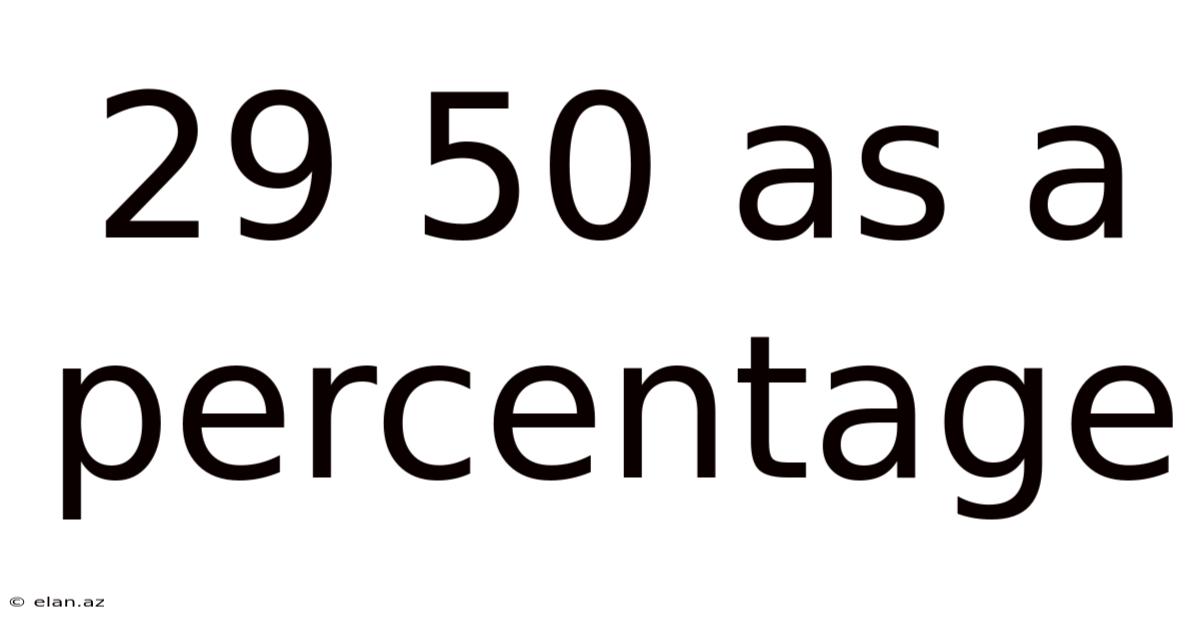
Table of Contents
Decoding 29/50 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to comprehending statistical data and financial reports. This article delves into the process of converting fractions to percentages, specifically focusing on how to express the fraction 29/50 as a percentage. We will not only provide the solution but also explore the underlying concepts, offering a comprehensive understanding for students, educators, and anyone seeking to enhance their mathematical proficiency. This guide includes practical examples, step-by-step instructions, and frequently asked questions, making the process clear and accessible for all.
Understanding Fractions and Percentages
Before diving into the conversion of 29/50 to a percentage, let's review the basic definitions. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates the total number of equal parts the whole is divided into.
A percentage is a way of expressing a fraction or ratio as a number out of 100. The term "percent" literally means "per hundred." Therefore, a percentage represents the proportion of a whole expressed as a fraction of 100. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or simplified, 1/2.
Converting Fractions to Percentages: A Step-by-Step Guide
The process of converting a fraction to a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator. In our case, we have the fraction 29/50. Therefore, we perform the division:
29 ÷ 50 = 0.58
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%). In our case:
0.58 × 100 = 58
Therefore, 0.58 is equal to 58%.
Conclusion: 29/50 as a Percentage
Following these steps, we can definitively state that 29/50 is equal to 58%.
Alternative Method: Using Equivalent Fractions
An alternative approach involves finding an equivalent fraction with a denominator of 100. Since percentages are based on 100, this method provides a direct conversion.
To find an equivalent fraction with a denominator of 100, we need to determine what number, when multiplied by 50, gives us 100. That number is 2 (50 x 2 = 100). To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by the same number:
(29 × 2) / (50 × 2) = 58/100
Since 58/100 means 58 out of 100, this directly translates to 58%. This method provides a clear visual representation of the percentage.
Real-World Applications of Percentage Conversions
The ability to convert fractions to percentages has numerous practical applications in various fields:
- Finance: Calculating interest rates, discounts, profit margins, and tax amounts. For example, if a store offers a 58% discount on an item, understanding this percentage is crucial for calculating the final price.
- Statistics: Representing data in a more easily understandable format. Percentages are commonly used to express proportions in surveys, polls, and statistical analyses. For example, if 29 out of 50 people surveyed preferred a particular product, representing this as 58% makes the result immediately clear.
- Science: Expressing concentrations, yields, and error rates. In scientific experiments, percentages are used to represent the success rate of an experiment or the concentration of a substance in a solution.
- Everyday Life: Calculating tips, sales tax, and understanding proportions in recipes. Understanding percentages makes daily calculations easier and faster, such as calculating a 15% tip at a restaurant.
Understanding Percentage Increase and Decrease
While this article focuses on converting a single fraction to a percentage, it’s important to also understand how percentages relate to increases and decreases. Consider the following scenarios:
- Percentage Increase: If you start with a value of 50 and increase it by 58%, you would calculate 50 x 0.58 = 29. Adding this increase to the original value gives you 50 + 29 = 79.
- Percentage Decrease: If you start with a value of 79 and decrease it by 58%, you would calculate 79 x 0.58 = 45.82. Subtracting this decrease from the original value gives you 79 - 45.82 = 33.18.
These calculations illustrate the practical use of percentages in determining changes in values.
Advanced Applications: Working with Percentages in Equations
Percentages can be incorporated into more complex mathematical equations. For example, if you're solving for an unknown value (x) in an equation that includes a percentage, you can use algebraic techniques to isolate and solve for x. Let's consider a simple example:
- x + 58% of x = 79
To solve this equation:
- Convert the percentage to a decimal: 58% = 0.58
- Rewrite the equation: x + 0.58x = 79
- Combine like terms: 1.58x = 79
- Solve for x: x = 79 / 1.58 ≈ 50
This example shows how understanding percentage conversions is essential for solving more advanced mathematical problems.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, absolutely. Any fraction can be converted to a percentage by following the steps outlined above: dividing the numerator by the denominator to obtain a decimal and then multiplying the decimal by 100 to get the percentage.
Q2: What if the decimal resulting from the division is very long?
A2: You can round the decimal to a certain number of decimal places to obtain a more manageable percentage. For example, if the decimal is 0.58333..., you could round it to 0.58 or 0.583, depending on the required level of precision.
Q3: Are there any online tools or calculators to help with this conversion?
A3: Yes, many online calculators are available that can quickly convert fractions to percentages. However, understanding the underlying process is crucial for developing a strong mathematical foundation.
Q4: Why is understanding percentages important?
A4: Percentages are fundamental for comprehending and applying mathematical concepts in various aspects of life, from personal finance to professional fields. A solid grasp of percentages allows for more informed decision-making and a deeper understanding of numerical data.
Q5: How can I improve my understanding of percentages?
A5: Practice is key. Try converting different fractions to percentages, working through examples, and seeking assistance when needed. You can also find numerous online resources, including videos and practice exercises, to further enhance your understanding.
Conclusion
Converting fractions to percentages is a vital mathematical skill with broad applicability. This article has provided a thorough explanation of how to convert 29/50 to its percentage equivalent (58%), along with detailed explanations, alternative methods, real-world applications, and frequently asked questions. Mastering this concept will significantly improve your ability to interpret and utilize numerical data in various contexts. Remember that consistent practice and a clear understanding of the underlying principles are key to mastering this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Electric Current Is Measured In
Sep 16, 2025
-
Simple Heart Diagram With Labels
Sep 16, 2025
-
1 100 In Decimal Form
Sep 16, 2025
-
Where Are Magnetic Fields Strongest
Sep 16, 2025
-
Animal That Starts With M
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 29 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.