3 20 As A Decimal
elan
Sep 16, 2025 · 5 min read
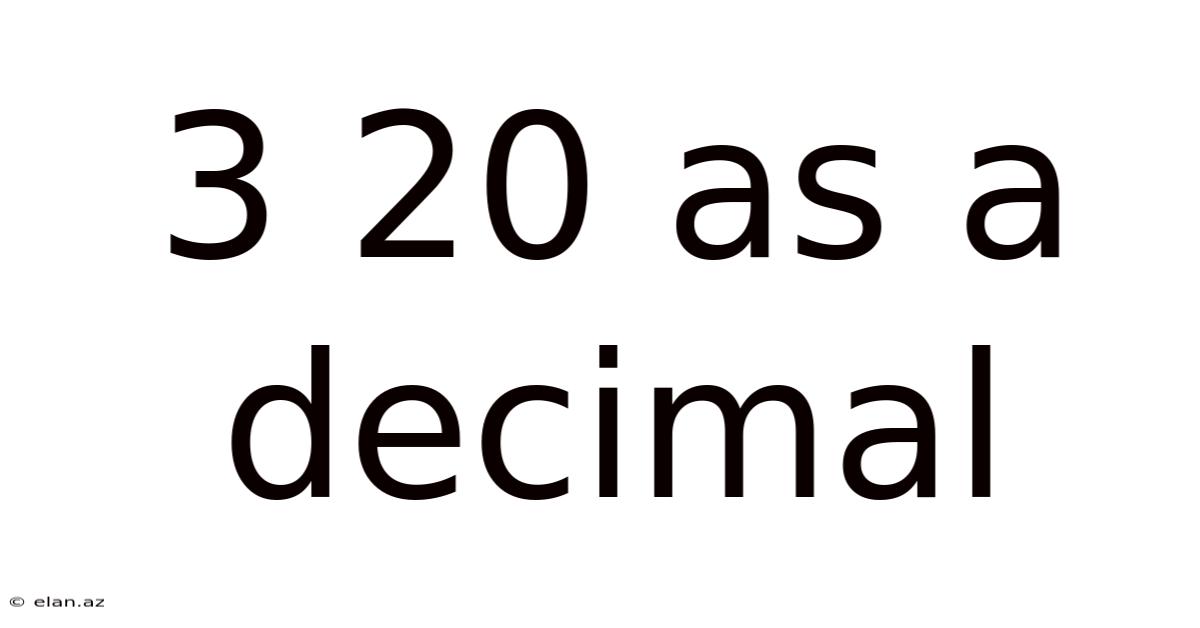
Table of Contents
Understanding 3 20 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article delves deep into the conversion of the mixed number 3 20 to its decimal equivalent, exploring the underlying principles and providing a step-by-step guide accessible to all levels. We'll also touch upon related concepts and answer frequently asked questions to ensure a comprehensive understanding. This guide aims to demystify the process and empower you with the confidence to tackle similar conversions independently.
Understanding Mixed Numbers and Decimals
Before we dive into the conversion, let's clarify the terms involved. A mixed number, like 3 20, combines a whole number (3 in this case) and a proper fraction (2/20). A decimal, on the other hand, represents a number using base-10, where the position of each digit represents a power of 10. For instance, 3.14 has 3 as the whole number and 14/100 (or 0.14) as the fractional part. Our goal is to express 3 20 as a decimal number with a whole number part and a fractional part expressed after a decimal point.
Step-by-Step Conversion of 3 20 to Decimal
The conversion process involves two key steps:
-
Convert the Fraction to a Decimal: The fraction 2/20 needs to be converted into its decimal equivalent. We achieve this by dividing the numerator (2) by the denominator (20):
2 ÷ 20 = 0.1
-
Combine the Whole Number and Decimal Part: Now, we combine the whole number part (3) from the mixed number with the decimal equivalent of the fraction (0.1) we just calculated:
3 + 0.1 = 3.1
Therefore, 3 20 as a decimal is 3.1.
Alternative Methods for Conversion
While the method above is straightforward, let's explore alternative approaches that can be useful in different scenarios:
-
Simplifying the Fraction: Before performing the division, simplifying the fraction can often make the calculation easier. In this case, we can simplify 2/20 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 2:
2/20 = (2 ÷ 2) / (20 ÷ 2) = 1/10
Now, converting 1/10 to a decimal is even simpler:
1 ÷ 10 = 0.1
We then add the whole number: 3 + 0.1 = 3.1
-
Using Decimal Equivalents of Common Fractions: Memorizing the decimal equivalents of common fractions (like 1/2 = 0.5, 1/4 = 0.25, 1/10 = 0.1, etc.) can significantly speed up the conversion process. Since 2/20 simplifies to 1/10, we directly know its decimal equivalent is 0.1.
-
Long Division: For more complex fractions, long division offers a reliable method. While not necessary for 2/20, understanding long division is crucial for tackling more challenging fraction-to-decimal conversions. The process involves repeatedly dividing the numerator by the denominator, adding zeros as needed, until you reach the desired level of accuracy or a repeating pattern emerges.
Understanding the Concept of Decimal Places
The number of digits after the decimal point is called the number of decimal places. In the case of 3.1, we have one decimal place. The value of each digit after the decimal point represents a power of 10. For example, in 3.1:
- The digit 1 in the tenths place represents 1/10 or 0.1.
- The digit 3 in the ones place represents 3 x 1 or 3.
Decimal Representation and Place Value
It's important to understand the relationship between decimal representation and place value. Each position to the right of the decimal point represents a decreasing power of 10: tenths, hundredths, thousandths, and so on. This system allows for the precise representation of fractional values. The number 3.1 can also be written as:
3 + 1/10 = 31/10
This highlights the connection between fractions and decimals, reinforcing the idea that they are simply different ways of representing the same numerical value.
Practical Applications of Decimal Conversion
Converting fractions to decimals is crucial in many real-world applications, including:
- Financial Calculations: Dealing with money often involves decimals. Converting fractional amounts (like shares of stock) to decimals is essential for accurate calculations.
- Measurement: Many measurement systems (metric system) utilize decimal notation. Converting fractional measurements to decimals ensures consistency and accurate calculations.
- Scientific Computations: Decimals are fundamental in scientific calculations, enabling precise representation of values and facilitating complex computations.
- Data Analysis: Data analysis often requires converting fractional data to decimals for statistical calculations and graph representation.
- Programming and Computing: Computers primarily use binary systems (base-2), but decimal representations are extensively used in programming languages and input/output operations for user-friendliness.
Frequently Asked Questions (FAQ)
Q: What if the fraction doesn't divide evenly?
A: Some fractions result in repeating decimals (e.g., 1/3 = 0.333...). In these cases, you can either round off to a desired number of decimal places or use a bar notation (e.g., 0.3̅) to indicate the repeating digit(s).
Q: How do I convert a decimal back to a fraction?
A: To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (10, 100, 1000, etc.), depending on the number of decimal places. Then simplify the fraction to its lowest terms. For instance, 0.25 can be written as 25/100, which simplifies to 1/4.
Q: Can I use a calculator for this conversion?
A: Yes, calculators can efficiently perform these conversions. Simply divide the numerator of the fraction by the denominator to obtain the decimal equivalent.
Q: Why is understanding decimal conversion important?
A: Decimal conversion is a critical skill for various applications, from everyday calculations to complex scientific and technological tasks. A strong understanding of this concept forms a solid foundation for further mathematical and scientific learning.
Conclusion
Converting 3 20 to its decimal equivalent, 3.1, is a straightforward process that underscores the fundamental relationship between fractions and decimals. Understanding the underlying principles, exploring different methods of conversion, and grasping the significance of decimal places will enhance your mathematical proficiency and provide you with the tools to confidently tackle similar conversions. The ability to fluently convert between fractions and decimals is an invaluable skill that will serve you well in various academic and professional endeavors. Remember to practice regularly to solidify your understanding and improve your speed and accuracy. This understanding of decimal conversions empowers you to tackle more complex mathematical problems and strengthens your overall mathematical literacy.
Latest Posts
Latest Posts
-
Meaning Of Silly In Urdu
Sep 16, 2025
-
What Is 2 Of 2000
Sep 16, 2025
-
Light Dependent Reaction Of Photosynthesis
Sep 16, 2025
-
Words That Have Three Syllables
Sep 16, 2025
-
Pictures Of Flowers To Draw
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 20 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.