3 20 As A Percent
elan
Sep 12, 2025 · 6 min read
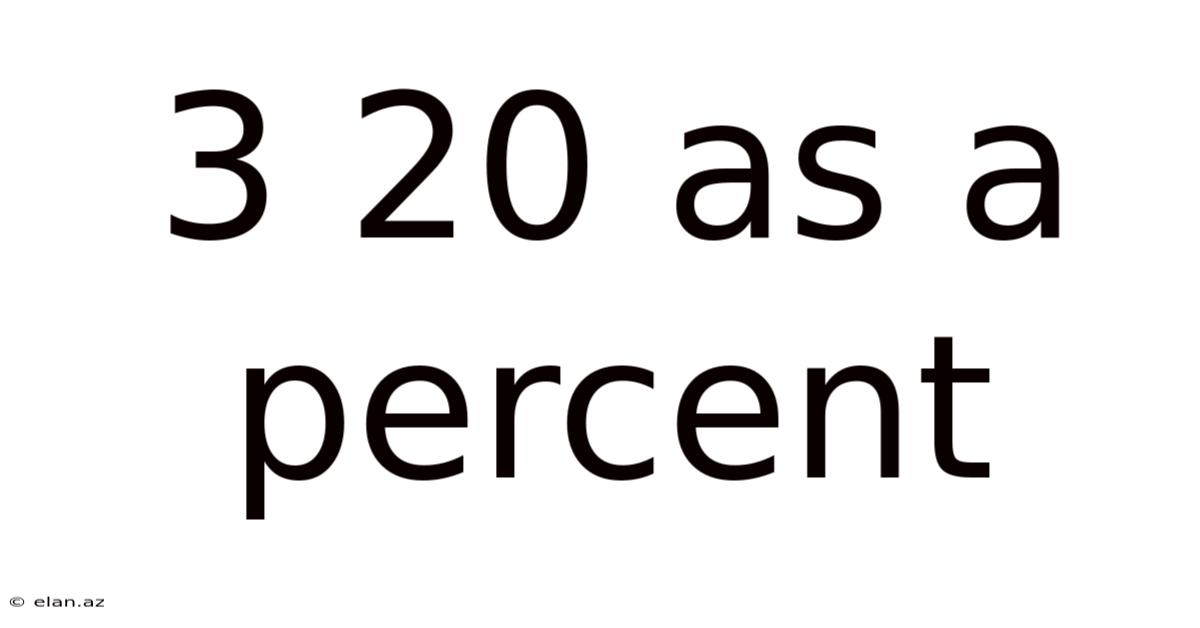
Table of Contents
Understanding 3/20 as a Percent: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 3/20 into a percentage, explaining the underlying principles and providing practical examples. We'll explore different methods, address common misconceptions, and even touch upon the broader implications of understanding fractional percentages. This will equip you with a solid grasp of this crucial mathematical concept.
Introduction: Fractions, Decimals, and Percentages – A Triad
Before we tackle the specific conversion of 3/20, let's clarify the relationship between fractions, decimals, and percentages. These three represent different ways of expressing the same numerical value, forming a triad easily interchangeable with basic mathematical operations.
-
Fractions: Represent a part of a whole, expressed as a ratio of two numbers (numerator/denominator). For example, 3/20 signifies 3 parts out of a total of 20 parts.
-
Decimals: Represent a part of a whole using base-10 notation, where a decimal point separates the whole number from fractional parts. Decimals are inherently linked to percentages as they represent parts of a hundred.
-
Percentages: Represent a part of a whole as a fraction of 100. The symbol "%" indicates "per hundred." A percentage is essentially a fraction with a denominator of 100.
Understanding these interrelationships is crucial for seamless conversion between the three formats.
Method 1: The Direct Conversion Method
This method involves directly converting the fraction into an equivalent fraction with a denominator of 100. This then allows for a direct read-off of the percentage.
To convert 3/20 to a percentage, we need to find an equivalent fraction with 100 as the denominator. We can achieve this by multiplying both the numerator and the denominator by the same number. Since 20 multiplied by 5 equals 100, we multiply both the numerator and the denominator of 3/20 by 5:
(3 * 5) / (20 * 5) = 15/100
Since a percentage is a fraction out of 100, 15/100 is directly equivalent to 15%. This is the simplest and most intuitive method for this specific fraction.
Method 2: The Decimal Conversion Method
This method involves first converting the fraction to a decimal and then converting the decimal to a percentage. This approach is generally more applicable when dealing with fractions that don't easily convert to a denominator of 100.
Step 1: Convert the fraction to a decimal.
To convert 3/20 to a decimal, we simply divide the numerator (3) by the denominator (20):
3 ÷ 20 = 0.15
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol.
0.15 * 100 = 15%
Therefore, 3/20 is equivalent to 15% using the decimal conversion method.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. This method is useful for understanding the underlying relationship and is easily adaptable for more complex fractions.
We can set up a proportion:
3/20 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
20x = 300
x = 300/20
x = 15
Therefore, 3/20 is equal to 15%.
Illustrative Examples and Real-World Applications
Let's consider some real-world scenarios where understanding 3/20 as 15% is beneficial:
-
Sales and Discounts: A store offers a 15% discount on an item. If the original price is $100, the discount amount is 15% of $100, which is $15. This is equivalent to a fraction of 15/100 or 3/20 of the original price.
-
Grade Calculation: A student answers 3 out of 20 questions correctly on a quiz. Their score is 15%, representing their performance relative to the total number of questions.
-
Statistical Analysis: In a survey of 20 people, 3 preferred a particular product. This represents a 15% preference rate for that product.
Addressing Common Misconceptions
-
Multiplying by 100%: Incorrect Approach: A common mistake is multiplying the fraction directly by 100%. While seemingly logical, this is incorrect. The correct approach involves either converting to a decimal first or finding an equivalent fraction with a denominator of 100.
-
Confusing Numerator and Denominator: It's crucial to remember that the numerator (3) represents the part, and the denominator (20) represents the whole. Incorrectly placing these values can lead to erroneous calculations.
-
Ignoring the Percentage Symbol: Always remember to add the "%" symbol after converting to a percentage; it's integral to representing the value correctly.
The Significance of Understanding Percentages
Understanding how to convert fractions to percentages isn't just about rote calculations; it's about developing a deeper understanding of numerical relationships. This ability is essential for:
-
Financial Literacy: Calculating interest rates, discounts, tax amounts, and understanding financial statements all rely on a solid grasp of percentages.
-
Data Analysis: Percentages are fundamental to interpreting and representing data in various fields, such as statistics, market research, and scientific studies.
-
Problem-Solving: Many real-world problems can be solved efficiently by converting fractions to percentages and then applying percentage-based calculations.
-
Everyday Life: From calculating tips in restaurants to understanding sale prices in shops, percentages are ubiquitous in our daily lives.
Frequently Asked Questions (FAQ)
-
Q: Can I convert any fraction to a percentage? A: Yes, any fraction can be converted to a percentage by dividing the numerator by the denominator and then multiplying by 100.
-
Q: What if the resulting decimal has many digits? A: You can round the decimal to a suitable number of decimal places depending on the required precision.
-
Q: Are there online calculators to help with this conversion? A: Yes, many online calculators are readily available for converting fractions to percentages. However, understanding the underlying process is crucial for problem-solving and critical thinking.
-
Q: Why is the percentage important in financial calculations? A: Percentages provide a standardized way to compare different financial values and calculate proportions easily, regardless of the original amounts involved.
Conclusion: Mastering the Art of Percentage Conversions
Converting fractions like 3/20 to percentages is a fundamental skill with widespread applicability. Through this guide, we've explored multiple methods—direct conversion, decimal conversion, and proportions—to achieve this transformation. Understanding the underlying principles, avoiding common misconceptions, and appreciating the real-world implications are key to mastering this essential mathematical skill. With practice and a clear understanding of the concepts, you'll confidently navigate the world of fractions, decimals, and percentages, empowering you to tackle a wide range of numerical challenges. Remember, the ability to convert between these formats is a building block for more advanced mathematical concepts and a valuable tool in many aspects of life.
Latest Posts
Latest Posts
-
Positive Words Starting With W
Sep 12, 2025
-
Lb Ft3 To Kg M3
Sep 12, 2025
-
Eukaryotic Cells A Level Biology
Sep 12, 2025
-
How Does Temperature Affect Humidity
Sep 12, 2025
-
5 Letter Word Starting Ha
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.