3 25 As A Percent
elan
Sep 17, 2025 · 5 min read
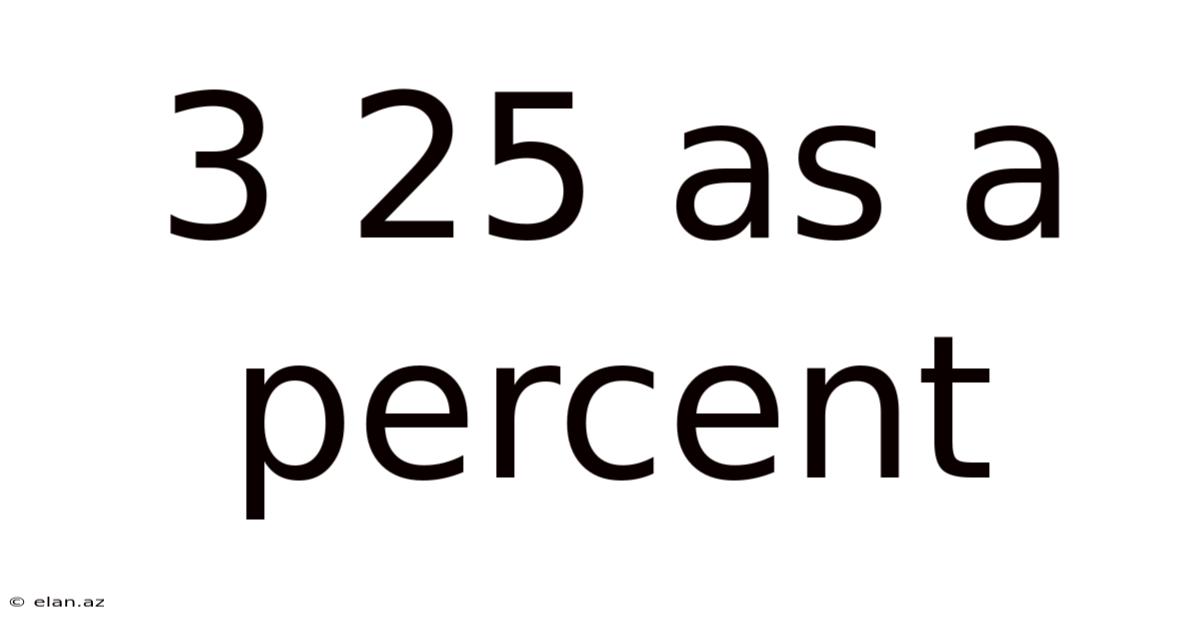
Table of Contents
Understanding 3/25 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life calculations. This comprehensive guide will delve into the process of converting the fraction 3/25 into a percentage, explaining the steps involved, providing illustrative examples, and exploring the underlying mathematical concepts. We will also address frequently asked questions (FAQs) to solidify your understanding. Understanding how to represent fractions as percentages is crucial for data interpretation, comparison, and problem-solving. This article will equip you with the knowledge and confidence to tackle similar fraction-to-percentage conversions.
Introduction: Fractions, Decimals, and Percentages
Before we dive into converting 3/25 into a percentage, let's briefly revisit the relationship between fractions, decimals, and percentages. These three forms represent proportions of a whole, but they use different notations.
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 3/25 indicates 3 parts out of a total of 25 parts.
-
Decimals: Represent a part of a whole using the base-ten number system. The decimal point separates the whole number from the fractional part.
-
Percentages: Represent a part of a whole as a proportion of 100. The symbol "%" denotes a percentage.
These three representations are interchangeable; you can convert one form into another without changing the underlying value. Understanding this interchangeability is key to mastering mathematical calculations involving proportions.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is perhaps the most common and straightforward method. It involves two steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, divide the numerator by the denominator. In our case:
3 ÷ 25 = 0.12
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
0.12 × 100 = 12%
Therefore, 3/25 is equal to 12%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the fact that percentages are always expressed as a proportion of 100. We can achieve this by finding an equivalent fraction of 3/25 that has a denominator of 100.
To do this, we need to determine what number, when multiplied by 25, gives us 100. This is 4 (25 x 4 = 100). Since we multiply the denominator by 4, we must also multiply the numerator by 4 to maintain the same value:
(3 x 4) / (25 x 4) = 12/100
Since 12/100 means 12 parts out of 100, this directly translates to 12%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We can set up a proportion where x represents the percentage we're looking for:
3/25 = x/100
To solve for x, we can cross-multiply:
25x = 300
Then, divide both sides by 25:
x = 300/25 = 12
Therefore, x = 12, meaning 3/25 is equal to 12%.
Illustrative Examples: Applying the Conversion
Let's explore a few real-world examples to demonstrate the practical application of converting 3/25 to a percentage:
Example 1: Test Scores:
Imagine you answered 3 out of 25 questions correctly on a quiz. Your score as a percentage would be 12%, calculated as (3/25) * 100 = 12%.
Example 2: Sales Commission:
Let's say you earn a commission of 3 dollars for every 25 dollars of sales. Your commission rate is 12%, calculated as (3/25) * 100 = 12%.
Example 3: Discount:
A store offers a discount of 3 dollars for every 25 dollars spent. The discount percentage is 12%, which is (3/25) * 100 = 12%.
Mathematical Explanation: The Underlying Principles
The conversion from fraction to percentage relies on the fundamental concept of ratios and proportions. A percentage is essentially a fraction with a denominator of 100. Therefore, converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100 or using a proportion to solve for the equivalent percentage. The multiplication by 100 in the decimal-to-percentage conversion simply scales the decimal value to represent the proportion out of 100.
Frequently Asked Questions (FAQs)
Q1: Can I convert any fraction to a percentage?
Yes, absolutely! Any fraction can be converted to a percentage by following the methods outlined above.
Q2: What if the fraction is an improper fraction (numerator > denominator)?
Even with improper fractions, the method remains the same. You divide the numerator by the denominator to obtain a decimal, which is then converted to a percentage. The resulting percentage will be greater than 100%.
Q3: Are there any shortcuts for converting fractions to percentages?
While the methods described are straightforward, some fractions might have easily recognizable decimal equivalents (e.g., 1/4 = 0.25 = 25%). Recognizing these can speed up the process. However, the methods discussed provide a reliable approach for any fraction.
Q4: Why is understanding percentage conversion important?
Percentage conversion is crucial for interpreting data, comparing proportions, calculating discounts, understanding interest rates, analyzing statistical data, and much more. It’s a fundamental skill across various disciplines.
Q5: What if I get a decimal answer that doesn't terminate?
Some fractions result in non-terminating decimals (like 1/3 = 0.333...). In such cases, you can round the decimal to a suitable number of decimal places before converting to a percentage. The level of precision required depends on the context of the problem.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a versatile mathematical skill with wide-ranging applications. The methods discussed in this article – converting to a decimal then to a percentage, finding an equivalent fraction with a denominator of 100, and using proportions – provide a comprehensive understanding of this crucial conversion. Mastering these methods will enhance your problem-solving capabilities in various numerical contexts and deepen your understanding of proportional relationships. Remember to practice regularly to build proficiency and confidence in handling fraction-to-percentage conversions. By understanding the underlying principles, you can effectively apply this knowledge to a wide range of real-world scenarios, from calculating discounts to analyzing financial data.
Latest Posts
Latest Posts
-
Times Table Colouring By Numbers
Sep 17, 2025
-
Search For My Tongue Poem
Sep 17, 2025
-
What Is An Acute Illness
Sep 17, 2025
-
British East India Company Coins
Sep 17, 2025
-
What Is The Business Activity
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.