3 3 3 X 3
elan
Sep 10, 2025 · 6 min read
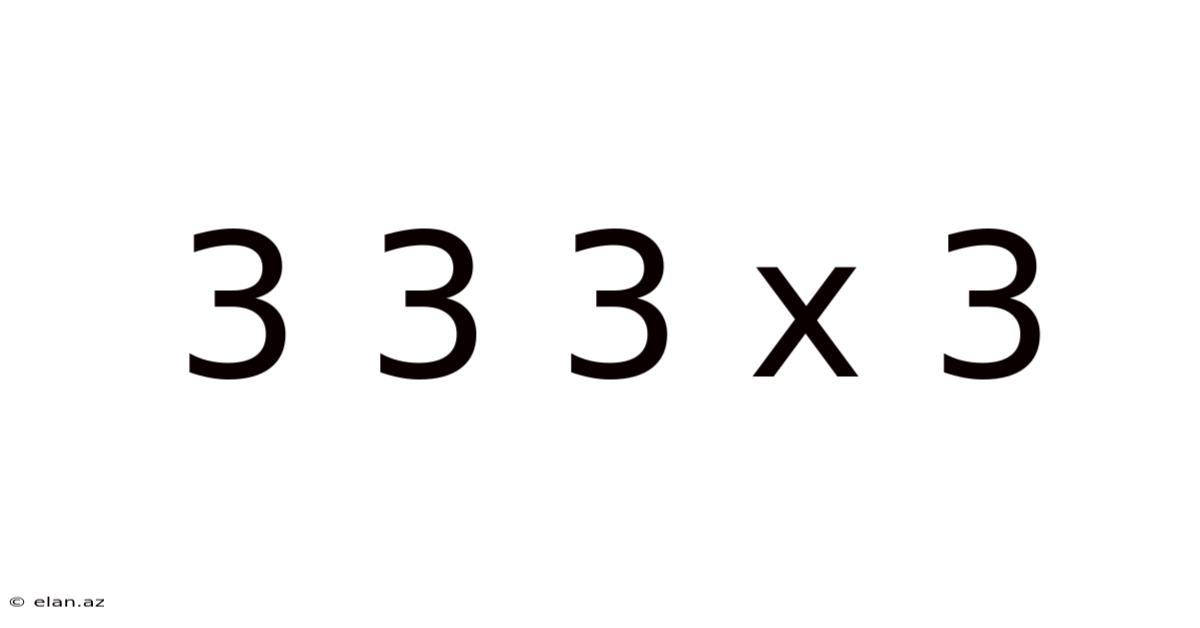
Table of Contents
Decoding 3 3 3 x 3: Exploring Mathematical Concepts and Problem-Solving Strategies
The seemingly simple expression "3 3 3 x 3" might initially appear straightforward. However, depending on the interpretation and application of mathematical operations, this expression can unlock a surprising range of solutions and delve into fascinating mathematical concepts. This article will explore the various ways we can interpret and solve this expression, emphasizing the importance of order of operations (PEMDAS/BODMAS), creative problem-solving, and the underlying mathematical principles. We'll delve into why understanding these concepts is crucial for mathematical proficiency and how seemingly simple problems can lead to complex and rewarding explorations.
Understanding Order of Operations (PEMDAS/BODMAS)
Before we tackle different interpretations of "3 3 3 x 3", it's crucial to understand the order of operations. This fundamental principle dictates the sequence in which mathematical operations should be performed to ensure consistent and accurate results. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) are common mnemonics used to remember the order. They essentially mean the same thing; the terminology differs slightly between regions.
In the absence of parentheses or exponents, multiplication and division are performed from left to right, followed by addition and subtraction, also from left to right. This is the cornerstone of solving our expression without any additional symbols or creative interpretation.
The Standard Interpretation: A Straightforward Solution
Without any further information or implied operations, the most straightforward interpretation of "3 3 3 x 3" is:
3 + 3 + 3 x 3
Following PEMDAS/BODMAS, we perform the multiplication first:
3 + 3 + 9
Then, we perform the addition:
3 + 3 + 9 = 15
Therefore, the standard interpretation of "3 3 3 x 3" yields a solution of 15. This is the most common and mathematically sound answer if the expression is presented without any additional context or implied operations.
Exploring Alternative Interpretations: Beyond the Standard
The beauty of mathematics lies in its ability to represent various concepts. While the standard interpretation is correct, we can explore alternative interpretations by introducing different mathematical operations or employing creative problem-solving strategies. This allows us to delve deeper into the realm of mathematical possibility and problem-solving skills.
1. Introducing Parentheses:
By strategically placing parentheses, we can significantly alter the result. For example:
(3 + 3 + 3) x 3 = 9 x 3 = 27
Here, the parentheses change the order of operations, prioritizing the addition before the multiplication, leading to a completely different solution. This highlights the crucial role that parentheses play in determining the result.
2. Using Concatenation (Joining Numbers):
While less common in standard mathematical notation, we could interpret the spaces as a form of concatenation, essentially joining the numbers together to create a single number. This would give us:
333 x 3 = 999
This interpretation, however, departs significantly from standard mathematical conventions and depends heavily on context or explicit instructions indicating this unusual approach.
3. Exploring Other Operations:
Let’s explore scenarios incorporating different operations. Although not present in the initial expression, we can add them for exploration:
- Subtraction: 33 - 3 x 3 = 33 - 9 = 24
- Division: 333 / 3 = 111
- Exponents: 3^3 + 3 x 3 = 27 + 9 = 36 (Note: this requires adding an exponent operation, demonstrating how different operations lead to drastically different results)
These examples showcase how seemingly minor modifications can dramatically impact the solution, thus emphasizing the significance of precision and clarity in mathematical notation.
The Importance of Clear Notation and Context
These alternative interpretations underscore the critical role of clear and unambiguous mathematical notation. The absence of parentheses or explicitly stated operations can lead to multiple valid interpretations. In a formal mathematical setting, ambiguity is undesirable; precision is paramount. Therefore, when working with mathematical expressions, it's always essential to ensure that the notation is clear, accurate, and free from any potential ambiguity.
Problem-Solving Strategies and Mathematical Thinking
Analyzing "3 3 3 x 3" beyond its basic solution cultivates crucial problem-solving skills. By experimenting with different approaches and interpretations, we develop:
- Critical Thinking: We learn to analyze the problem from various angles, considering different operational possibilities.
- Creative Problem Solving: We move beyond the standard approach, exploring creative solutions and pushing the boundaries of our mathematical understanding.
- Understanding Order of Operations: We reinforce the importance of PEMDAS/BODMAS, realizing how its application drastically affects the outcome.
- Mathematical Fluency: We strengthen our understanding of basic mathematical operations and their interplay.
Expanding the Concept: Similar Problems and Applications
The principles illustrated by "3 3 3 x 3" extend to more complex mathematical scenarios. Similar problems involving varying numbers and operations can be used to further solidify our understanding of order of operations and problem-solving strategies. These skills are not only crucial for academic success in mathematics but also for many real-world applications, including:
- Computer Programming: Order of operations is essential in programming to ensure accurate execution of code.
- Engineering and Physics: Precise calculations involving multiple operations are vital in these fields.
- Finance and Accounting: Accurate calculations are critical for financial modeling and analysis.
- Data Analysis: Understanding order of operations is important for correctly interpreting and manipulating data.
Frequently Asked Questions (FAQ)
Q: What is the only correct answer to "3 3 3 x 3"?
A: Without additional context or parentheses, the only mathematically correct answer adhering to standard order of operations (PEMDAS/BODMAS) is 15. However, alternative interpretations exist depending on the assumed context and the allowed mathematical operations.
Q: Why are parentheses so important in mathematics?
A: Parentheses dictate the order of operations, ensuring that calculations are performed in the correct sequence. They remove ambiguity and guarantee a consistent result.
Q: Can we use other mathematical operations besides addition, subtraction, multiplication, and division?
A: Yes. In more advanced contexts, we can incorporate other operations such as exponents, logarithms, and trigonometric functions. This extends the range of possible solutions and allows us to explore more complex mathematical concepts.
Q: What are some real-world applications of understanding order of operations?
A: Order of operations is crucial in computer programming, engineering, physics, finance, accounting, and data analysis, among other fields.
Conclusion: Embracing the Power of Mathematical Exploration
The seemingly simple expression "3 3 3 x 3" serves as a powerful reminder of the importance of clear mathematical notation, the significance of order of operations, and the power of creative problem-solving. While the standard solution is 15, exploring alternative interpretations reveals a wealth of mathematical concepts and enhances our problem-solving skills. This exploration emphasizes that mathematics is not just about finding answers; it's about understanding the underlying principles, exploring different perspectives, and appreciating the beauty of mathematical reasoning. By embracing these principles, we develop not just mathematical proficiency, but also valuable critical thinking and problem-solving skills applicable far beyond the realm of mathematics itself. Continue exploring, questioning, and experimenting – the world of mathematics is vast and endlessly rewarding.
Latest Posts
Latest Posts
-
Words Ending In A D
Sep 10, 2025
-
Stack Of Hay Crossword Clue
Sep 10, 2025
-
Convert Square Centimeters To Meters
Sep 10, 2025
-
Parts Of The Plant Labeled
Sep 10, 2025
-
1 5 Kg Converted To Pounds
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3 3 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.