3 4 X 1 2
elan
Sep 16, 2025 · 6 min read
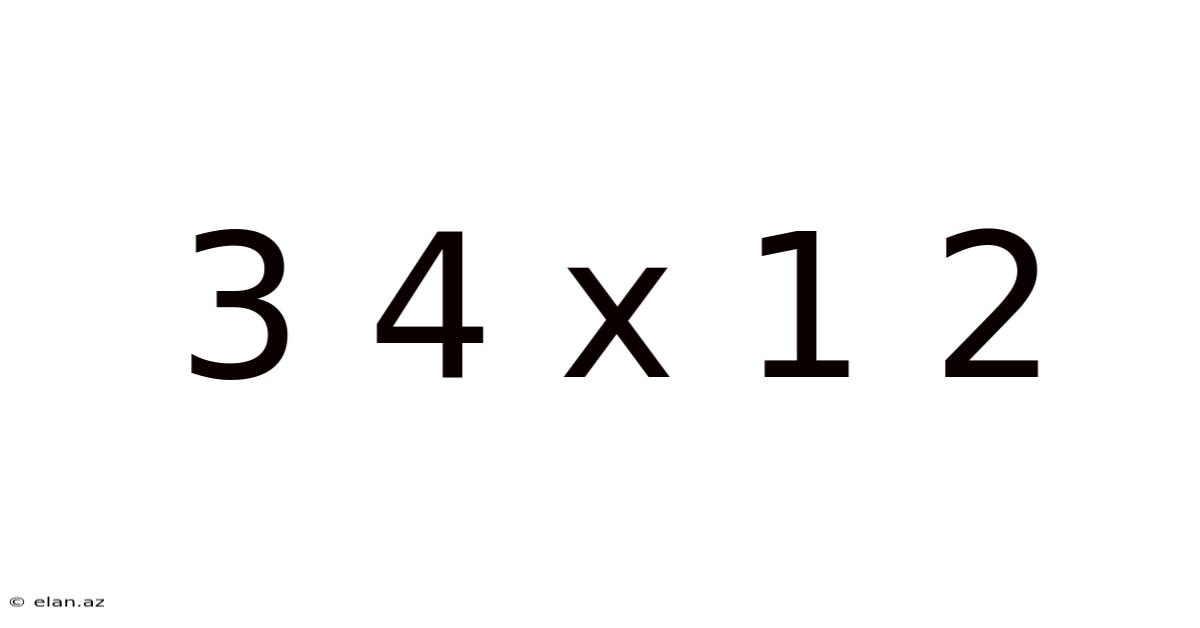
Table of Contents
Decoding 3/4 x 1/2: A Deep Dive into Fraction Multiplication
Understanding fraction multiplication can seem daunting at first, but with a clear approach and a little practice, it becomes surprisingly straightforward. This comprehensive guide breaks down the seemingly simple problem of 3/4 x 1/2, exploring the underlying principles, different methods of solving it, and expanding upon the concepts to tackle more complex fraction calculations. This article will equip you with the knowledge and confidence to conquer any fraction multiplication problem you encounter.
Introduction: What Does 3/4 x 1/2 Even Mean?
The expression "3/4 x 1/2" represents the multiplication of two fractions: three-quarters and one-half. Before we delve into the methods of calculation, it's crucial to grasp the conceptual meaning. Imagine you have a pizza cut into four equal slices. You possess three of those slices (3/4 of the pizza). Now, imagine you want to find out what half (1/2) of your three slices is. That's precisely what this multiplication problem calculates: finding a portion of a portion. This understanding forms the basis of all fraction multiplication.
Method 1: The Straightforward Approach: Multiply Numerators and Denominators
The most common and efficient method for multiplying fractions is to multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together separately. Let's apply this to our problem:
- Step 1: Multiply the numerators: 3 x 1 = 3
- Step 2: Multiply the denominators: 4 x 2 = 8
- Step 3: Combine the results to form the new fraction: 3/8
Therefore, 3/4 x 1/2 = 3/8. This means that half of three-quarters is three-eighths.
Method 2: Visual Representation: Using Area Models
A visual approach can be particularly helpful for understanding the concept of fraction multiplication, especially for beginners. Let's visualize 3/4 x 1/2 using an area model:
- Draw a square: This square represents the whole, or 1.
- Divide the square into four equal parts horizontally: This represents the fraction 3/4. Shade three of these parts to visually represent 3/4.
- Divide the square into two equal parts vertically: This represents the fraction 1/2.
- Identify the overlapping area: The overlapping area represents the product of 3/4 and 1/2. You'll notice that this overlapping area constitutes 3 out of 8 equal parts of the original square.
This visual representation clearly shows that 3/4 x 1/2 = 3/8. This method helps solidify the concept and makes it easier to understand the result intuitively.
Method 3: Simplifying Before Multiplication (Cancellation)
Sometimes, before multiplying the numerators and denominators, you can simplify the fractions by cancelling common factors. This makes the calculation easier and often results in a simplified final answer. This method involves finding common factors between the numerators and denominators. However, in the case of 3/4 x 1/2, there are no common factors between the numerators and denominators, so simplification before multiplication isn't possible in this specific instance. Let's look at an example where this technique is useful:
Consider the problem: (3/6) x (2/4). Notice that 3 and 6 share a common factor of 3 (3/3 = 1, 6/3 = 2), and 2 and 4 share a common factor of 2 (2/2 = 1, 4/2 = 2). We can simplify before multiplying:
(3/6) x (2/4) = (1/2) x (1/2) = 1/4
This demonstrates how simplifying before multiplication can streamline the process and prevent dealing with larger numbers.
Expanding the Concepts: Multiplying More Than Two Fractions
The principles of fraction multiplication extend seamlessly to multiplying more than two fractions. You simply multiply all the numerators together and all the denominators together. For instance:
(1/2) x (2/3) x (3/4) = (1 x 2 x 3) / (2 x 3 x 4) = 6/24
Notice that even here, you can simplify the result by dividing both the numerator and denominator by their greatest common factor (6), resulting in 1/4.
Working with Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 1 1/2). To multiply mixed numbers, you first convert them into improper fractions. An improper fraction has a numerator larger than or equal to the denominator.
For example, to multiply 1 1/2 by 2/3:
- Convert the mixed number to an improper fraction: 1 1/2 = (1 x 2 + 1) / 2 = 3/2
- Multiply the improper fractions: (3/2) x (2/3) = 6/6 = 1
This shows how converting mixed numbers into improper fractions allows you to apply the standard fraction multiplication method.
The Significance of Understanding Fraction Multiplication
Mastering fraction multiplication is fundamental to success in mathematics, particularly in algebra and beyond. It’s a cornerstone skill applicable across numerous fields, including:
- Cooking and Baking: Scaling recipes up or down requires accurate fraction manipulation.
- Construction and Engineering: Precise measurements and calculations often involve fractions.
- Finance: Calculating percentages, interest rates, and shares involves fraction operations.
- Science: Many scientific calculations and measurements rely on precise fractional values.
A strong understanding of fraction multiplication is not just about solving mathematical problems; it's about developing a crucial problem-solving skill applicable to numerous real-world situations.
Frequently Asked Questions (FAQ)
Q1: What if one of the fractions is a whole number?
A1: Consider a whole number as a fraction with a denominator of 1. For example, 2 x 1/3 can be written as (2/1) x (1/3) = 2/3.
Q2: How do I simplify fractions after multiplication?
A2: Find the greatest common factor (GCF) of the numerator and denominator. Divide both the numerator and denominator by the GCF to obtain the simplified fraction.
Q3: What if the result is an improper fraction?
A3: Convert the improper fraction to a mixed number. For example, 7/4 can be converted to 1 3/4.
Q4: Are there online calculators or tools to help with fraction multiplication?
A4: Yes, many online calculators and tools are available to assist with fraction multiplication and other mathematical operations. However, understanding the underlying principles is crucial for true mathematical proficiency.
Conclusion: Mastering Fraction Multiplication
Understanding and mastering fraction multiplication is a critical step in developing strong mathematical skills. While the process might seem intimidating initially, the straightforward methods outlined in this guide, coupled with consistent practice and the use of visual aids, will equip you with the ability to confidently tackle any fraction multiplication problem. Remember that the key is understanding the underlying concept of finding a portion of a portion. With practice and patience, you'll transform this seemingly complex concept into a fundamental and easily manageable skill. Don't hesitate to review these methods and practice regularly to solidify your understanding and build confidence in your ability to conquer the world of fractions.
Latest Posts
Latest Posts
-
Dot Cross Diagram Magnesium Oxide
Sep 16, 2025
-
1 X 1 X Expansion
Sep 16, 2025
-
Steps In Sliding Filament Theory
Sep 16, 2025
-
Waste And Types Of Waste
Sep 16, 2025
-
Simultaneous Equations With A Quadratic
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 4 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.