33 50 As A Percent
elan
Sep 21, 2025 · 5 min read
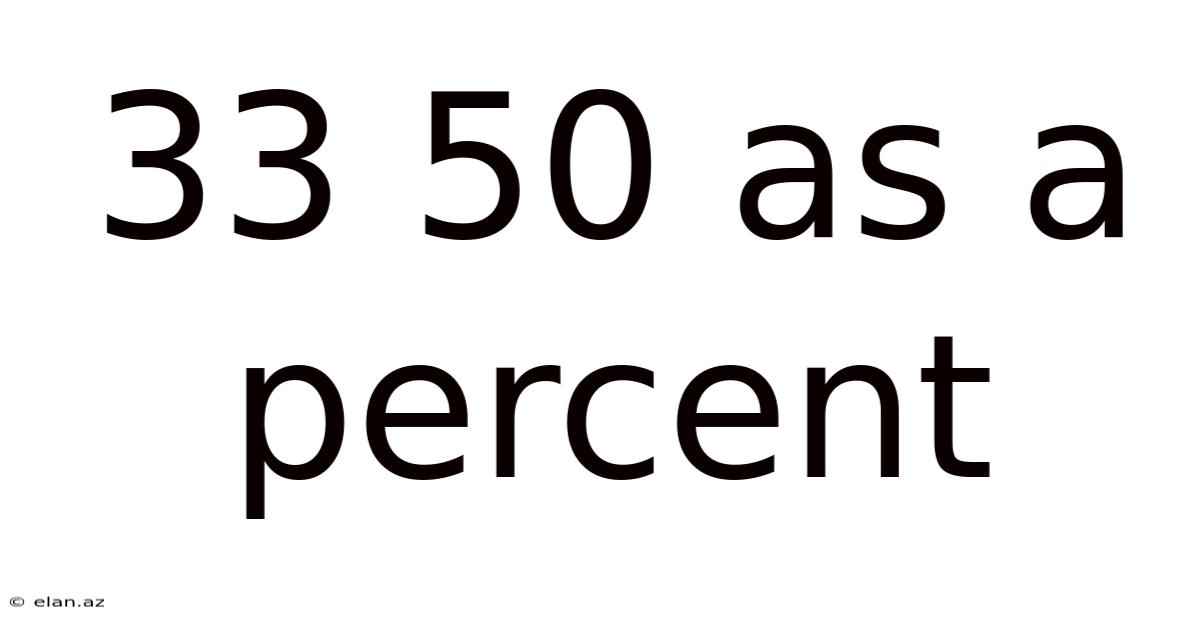
Table of Contents
33/50 as a Percent: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various fields, from everyday finances to complex scientific calculations. This article provides a comprehensive guide to converting fractions to percentages, focusing specifically on expressing 33/50 as a percentage. We'll delve into the method, explore its practical applications, and address common related questions. This guide is designed for learners of all levels, ensuring clarity and a strong understanding of the concept.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." Therefore, to express any fraction as a percentage, we need to find its equivalent fraction with a denominator of 100. This process involves understanding the relationship between fractions, decimals, and percentages, all of which represent proportional parts of a whole.
Converting 33/50 to a Percentage: The Step-by-Step Approach
The most straightforward method to convert 33/50 to a percentage is to multiply the fraction by 100%. This is because multiplying by 100% is equivalent to multiplying by 1 (since 100%/100% = 1), which doesn't change the value of the fraction, only its representation.
Here's a step-by-step breakdown:
-
Write the fraction: We start with the fraction 33/50.
-
Multiply by 100%: We multiply the fraction by 100%: (33/50) * 100%
-
Simplify: Now we simplify the expression. The 50 in the denominator divides into 100 two times (100/50 = 2).
-
Calculate the Result: This leaves us with 33 * 2% = 66%
Therefore, 33/50 is equal to 66%.
Alternative Method: Converting to Decimal First
Another approach involves first converting the fraction to a decimal and then converting the decimal to a percentage.
-
Divide the numerator by the denominator: Divide 33 by 50: 33 ÷ 50 = 0.66
-
Multiply by 100: Multiply the decimal by 100: 0.66 * 100 = 66
-
Add the percentage symbol: Add the percentage symbol to obtain the final answer: 66%
This method confirms our earlier result: 33/50 is equivalent to 66%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are a few examples:
-
Calculating Grades: If a student scores 33 out of 50 on a test, their percentage score is 66%.
-
Financial Calculations: Percentages are essential for understanding interest rates, discounts, taxes, and profit margins. For example, a 66% discount on a $100 item means a saving of $66.
-
Data Analysis: In statistics and data analysis, percentages are used to represent proportions and trends within datasets. For instance, if a survey shows that 33 out of 50 respondents prefer a particular product, this translates to a 66% preference rate.
-
Scientific Applications: Percentages are used extensively in scientific fields like chemistry, physics, and biology to express concentrations, yields, and error margins.
-
Everyday Life: Calculating tips, sales tax, and understanding price increases or decreases all involve working with percentages.
Advanced Concepts and Related Calculations
While converting 33/50 to a percentage is relatively straightforward, let's explore some related concepts that build upon this fundamental understanding.
-
Percentage Increase/Decrease: Suppose a value increases from 50 to 83. To find the percentage increase, first calculate the difference (83 - 50 = 33), then divide the difference by the original value (33/50) and multiply by 100%. This yields a 66% increase. Similar calculations apply to percentage decreases.
-
Finding the Original Value: If a value has been increased by a certain percentage, we can work backward to find the original value. For example, if a value is 83 after a 66% increase, we can set up an equation: Original Value * 1.66 = 83. Solving for the Original Value gives us 50.
-
Compound Percentages: These involve calculating percentages on percentages. For example, if a value increases by 10% and then by another 20%, the final result isn't simply a 30% increase. Compound percentages require sequential calculations.
-
Calculating Percentages of Percentages: This often involves multiplying fractions. For example, finding 20% of 66% would be calculated as (20/100) * (66/100) = 0.132 or 13.2%.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to understand percentages?
- A: Percentages provide a standardized way to compare proportions and make calculations easier to understand and interpret across various contexts. They are fundamental to understanding many aspects of daily life and various professional fields.
-
Q: Can I use a calculator to convert fractions to percentages?
- A: Yes, most calculators have a percentage function that simplifies this process. You can directly input the fraction (33/50) and use the percentage function to obtain the result.
-
Q: What if the fraction doesn't easily convert to a whole number percentage?
- A: In such cases, you'll get a decimal percentage. For example, 37/50 would result in 74%. Some fractions will result in repeating decimals, such as 1/3 which is approximately 33.33%. You would then round the decimal to an appropriate number of significant figures depending on the context.
-
Q: Are there any online tools that can help with percentage calculations?
- A: Yes, many websites and apps offer free online calculators specifically designed to perform various percentage calculations, including fraction-to-percentage conversions.
-
Q: How can I improve my understanding of percentages?
- A: Practice is key! Try working through various examples, both simple and complex. Utilize online resources, tutorials, and practice problems to solidify your understanding.
Conclusion: Mastering Percentage Calculations
Converting 33/50 to a percentage, which equals 66%, highlights the fundamental process of converting fractions to percentages. This seemingly simple calculation forms the basis for a broad range of applications across diverse fields. By understanding the underlying principles and practicing various related calculations, you'll develop a strong command of percentages, empowering you to solve practical problems and interpret data with confidence. Remember that mastering percentages isn't just about performing calculations; it's about gaining a deeper understanding of proportional relationships and their significance in the world around us. The ability to convert fractions to percentages is a vital skill that will serve you well in numerous aspects of your personal and professional life. Continue practicing, and you'll find yourself comfortable and confident in handling percentage calculations in any situation.
Latest Posts
Latest Posts
-
How To Use A Barometer
Sep 21, 2025
-
Packet Switching In Computer Networks
Sep 21, 2025
-
5 Letter Word Ends Ate
Sep 21, 2025
-
Easy Drawing Of A Squirrel
Sep 21, 2025
-
3 To The Zero Power
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 33 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.