35 60 As A Percentage
elan
Sep 21, 2025 · 5 min read
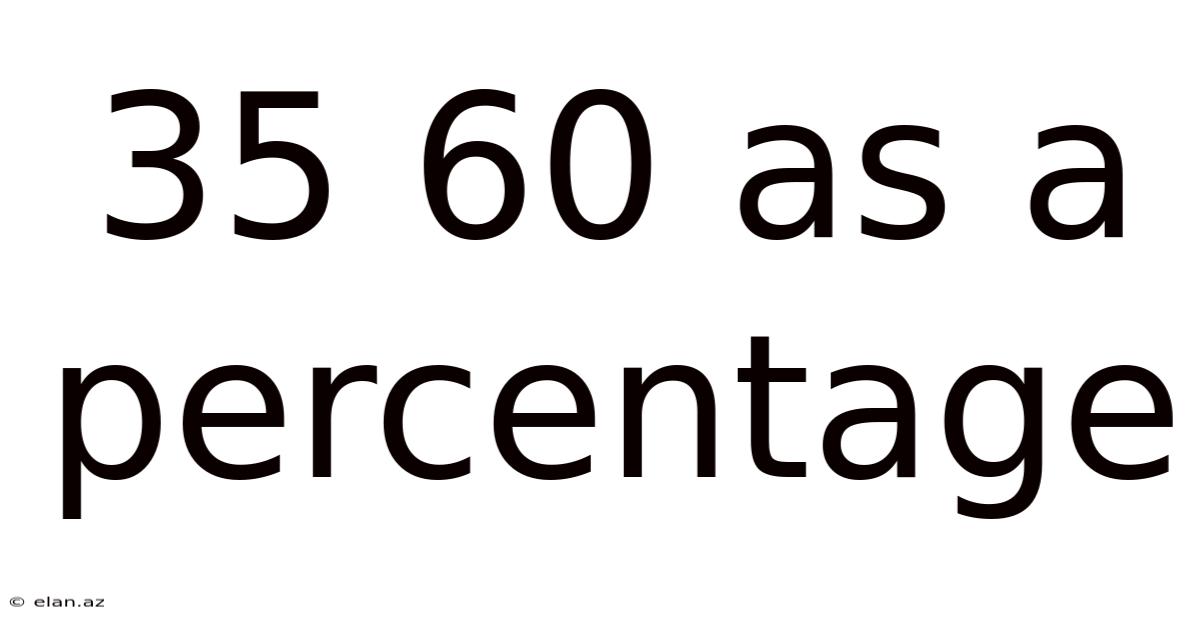
Table of Contents
35 of 60 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and sales tax to analyzing data and understanding financial reports. This article will delve into the process of calculating 35 out of 60 as a percentage, providing a step-by-step guide, exploring the underlying mathematical principles, and offering practical examples to solidify your understanding. We'll also address common questions and misconceptions surrounding percentage calculations. By the end, you’ll not only know the answer but also possess a deeper understanding of percentage calculations in general.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per cent" in Latin). For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively because they provide a standardized way to compare proportions and make comparisons easier to understand.
Calculating 35 out of 60 as a Percentage: A Step-by-Step Guide
To determine what percentage 35 represents of 60, we can follow these simple steps:
Step 1: Set up the Fraction
First, represent the problem as a fraction: 35/60. This fraction represents the portion (35) out of the total (60).
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
35 ÷ 60 = 0.583333...
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent symbol (%):
0.583333... × 100% = 58.3333...%
Step 4: Rounding
Since we are dealing with a repeating decimal, we usually round the percentage to a specific number of decimal places. Rounding to two decimal places, we get:
58.33%
Therefore, 35 out of 60 is 58.33%.
Alternative Calculation Method: Using Proportions
Another way to approach this problem is using proportions. We can set up a proportion where x represents the percentage we want to find:
35/60 = x/100
To solve for x, cross-multiply:
60x = 3500
Then, divide both sides by 60:
x = 3500/60 = 58.3333...
Again, rounding to two decimal places gives us 58.33%.
Mathematical Explanation: Understanding the Underlying Principles
The method outlined above uses the fundamental concept of ratios and proportions. A ratio compares two quantities, and a proportion states that two ratios are equal. In our case, the ratio of 35 to 60 is equal to the ratio of x to 100 (where x represents the percentage). The process of solving for x involves manipulating this equation to isolate the variable. This principle applies to all percentage calculations, making it a crucial concept to grasp.
Practical Applications: Real-World Examples
Percentage calculations are ubiquitous in daily life. Here are some examples demonstrating the practical use of the concept learned above:
- Grade Calculation: If a student answers 35 questions correctly out of a total of 60 questions on a test, their score would be 58.33%.
- Sales and Discounts: A store offering a 35% discount on an item originally priced at $60 would reduce the price by $21 ($60 x 0.35 = $21), resulting in a final price of $39.
- Survey Results: If 35 out of 60 respondents in a survey answered "yes" to a particular question, 58.33% of the respondents answered affirmatively.
- Financial Analysis: In financial statements, percentages are often used to represent proportions of total revenue, expenses, or assets. For example, if a company's operating expenses are $35 million out of a total revenue of $60 million, operating expenses represent 58.33% of total revenue.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage with a different numerator and denominator?
A: The method remains the same. Simply replace 35 and 60 with your new numbers, and follow the steps: (numerator/denominator) * 100%.
Q: Can I use a calculator for this calculation?
A: Absolutely! Calculators significantly simplify the process. Simply divide the numerator by the denominator and then multiply by 100.
Q: How do I handle percentages greater than 100%?
A: Percentages greater than 100% occur when the numerator is larger than the denominator. For instance, if you have 60 out of 35, the calculation would be (60/35) * 100% = 171.43%. This signifies that the numerator exceeds the denominator.
Q: What is the significance of rounding in percentage calculations?
A: Rounding helps to present the percentage in a clear, concise, and easily understandable manner. The level of precision required for rounding depends on the context. For informal calculations, rounding to one or two decimal places is typically sufficient. However, in scientific or financial contexts, more precise rounding may be necessary.
Q: Why is understanding percentages important?
A: Understanding percentages is vital for interpreting data, making informed decisions, and navigating everyday financial situations. From interpreting survey results to understanding financial reports, percentages are a cornerstone of quantitative literacy.
Conclusion
Calculating 35 out of 60 as a percentage results in 58.33%. This article has provided a detailed walkthrough of the calculation process, explored the underlying mathematical principles, and showcased its practical applications across diverse contexts. By mastering percentage calculations, you equip yourself with a valuable tool for tackling numerous real-world problems and interpreting quantitative information effectively. Remember that understanding the fundamental concept of ratios and proportions is key to solving various percentage-related problems, regardless of the specific numbers involved. Practice makes perfect, so try calculating different percentages to reinforce your learning and build confidence in your ability to handle these essential mathematical concepts.
Latest Posts
Latest Posts
-
200 Deg F To C
Sep 21, 2025
-
Gross Motor Function Classification System
Sep 21, 2025
-
400 Sq Feet In Meters
Sep 21, 2025
-
How To Use A Colorimeter
Sep 21, 2025
-
Table Of Results For Titration
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 35 60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.