36/14 As A Mixed Number
elan
Sep 23, 2025 · 5 min read
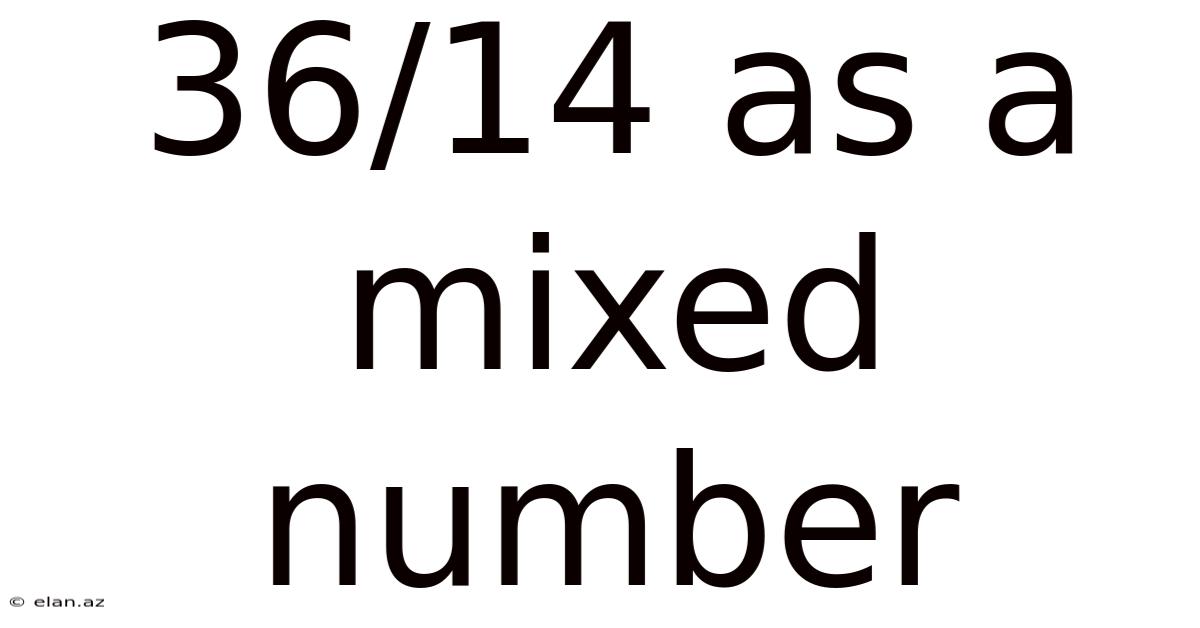
Table of Contents
Understanding 36/14 as a Mixed Number: A Comprehensive Guide
The conversion of improper fractions, like 36/14, into mixed numbers is a fundamental concept in arithmetic. This guide will thoroughly explore the process of transforming 36/14 into a mixed number, explaining the underlying principles and providing practical examples to solidify your understanding. We'll also delve into the importance of this conversion and address frequently asked questions. Mastering this skill will not only improve your fraction manipulation abilities but also enhance your problem-solving skills in various mathematical contexts.
Introduction: What are Mixed Numbers?
A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator (the top number) smaller than the denominator (the bottom number), representing a part of a whole. An improper fraction, on the other hand, has a numerator greater than or equal to the denominator, indicating a value greater than or equal to one. The improper fraction 36/14 represents more than one whole. Converting it to a mixed number helps visualize and understand its magnitude more clearly.
Converting 36/14 to a Mixed Number: A Step-by-Step Approach
The conversion of 36/14 involves dividing the numerator (36) by the denominator (14). This division will give us the whole number part of the mixed number and the remainder will become the numerator of the proper fraction.
Step 1: Perform the Division
Divide 36 by 14:
36 ÷ 14 = 2 with a remainder of 8
Step 2: Identify the Whole Number and the Remainder
From the division, we get:
- Quotient (Whole Number): 2
- Remainder: 8
Step 3: Construct the Mixed Number
The whole number (2) becomes the whole number part of the mixed number. The remainder (8) becomes the numerator of the proper fraction, and the denominator remains the same (14). Therefore, the mixed number representation of 36/14 is:
2 8/14
Simplifying the Mixed Number
While 2 8/14 is a correct mixed number representation of 36/14, it can be simplified further. To simplify, we need to find the greatest common divisor (GCD) of the numerator (8) and the denominator (14) of the fractional part. The GCD of 8 and 14 is 2. Dividing both the numerator and the denominator by 2, we get:
8 ÷ 2 = 4 14 ÷ 2 = 7
Therefore, the simplified mixed number is:
2 4/7
This simplified form is preferred because it represents the same value in a more concise and manageable way.
The Mathematical Explanation Behind the Conversion
The conversion from an improper fraction to a mixed number is based on the fundamental principle of representing quantities in different forms while maintaining their equivalence. Let's break down the process mathematically:
The improper fraction 36/14 can be rewritten as the sum of two fractions:
36/14 = (14/14) + (14/14) + (8/14)
Since 14/14 = 1 (one whole), the equation becomes:
36/14 = 1 + 1 + 8/14
This simplifies to:
36/14 = 2 + 8/14 = 2 8/14
This demonstrates that the process of dividing the numerator by the denominator and using the quotient and remainder to form a mixed number is a direct consequence of breaking down the improper fraction into a sum of whole numbers and a proper fraction.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in real-world scenarios where representing quantities as whole units and fractional parts is beneficial. Consider these examples:
- Measurements: If you have 2 4/7 meters of fabric, it's clearer to express it as a mixed number than as an improper fraction (18/7 meters).
- Baking: Recipes often use mixed numbers to specify ingredient quantities, like 1 1/2 cups of flour or 2 2/3 teaspoons of baking powder.
- Time: We commonly use mixed numbers when dealing with time, such as 1 hour and 30 minutes (1 1/2 hours).
- Construction: Measurements in construction projects, whether it's lumber lengths or wall dimensions, are often represented using mixed numbers for clarity and practicality.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying the mixed number important?
A1: Simplifying a mixed number makes it easier to understand and work with. A simplified fraction is more concise and reduces the risk of errors in calculations involving the fraction. For example, 2 4/7 is easier to manipulate in further calculations than 2 8/14.
Q2: Can I convert a mixed number back into an improper fraction?
A2: Yes, absolutely! To convert a mixed number (like 2 4/7) back to an improper fraction, multiply the whole number by the denominator and add the numerator. Keep the same denominator. In this case: (2 * 7) + 4 = 18, so the improper fraction is 18/7.
Q3: What if the remainder is zero after the division?
A3: If the remainder is zero after dividing the numerator by the denominator, the improper fraction is a whole number. There is no fractional part in the mixed number. For instance, 28/7 = 4, which is a whole number and doesn't require a mixed number representation.
Q4: Are there any other methods to convert an improper fraction to a mixed number?
A4: While the long division method is the most common and straightforward, you can also visualize the conversion using fraction circles or bars. This visual approach can be helpful for beginners to understand the concept of whole numbers and fractional parts within the improper fraction.
Conclusion: Mastering Mixed Numbers
Converting improper fractions to mixed numbers is a crucial skill in mathematics. Understanding this process not only allows for accurate calculations but also enhances your ability to interpret and represent quantitative information in a clear and concise manner. By following the steps outlined and practicing regularly, you will master this concept and confidently apply it in various mathematical and real-world contexts. Remember the key steps: divide, identify the whole number and remainder, and construct the simplified mixed number. This fundamental skill will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Different Types Of Organisational Structures
Sep 23, 2025
-
Use Immediately In A Sentence
Sep 23, 2025
-
Best Christmas Present For Husband
Sep 23, 2025
-
Are Fish Cold Blooded Animals
Sep 23, 2025
-
8th Letter Of The Alphabet
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 36/14 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.