5 20 As A Percent
elan
Sep 20, 2025 · 5 min read
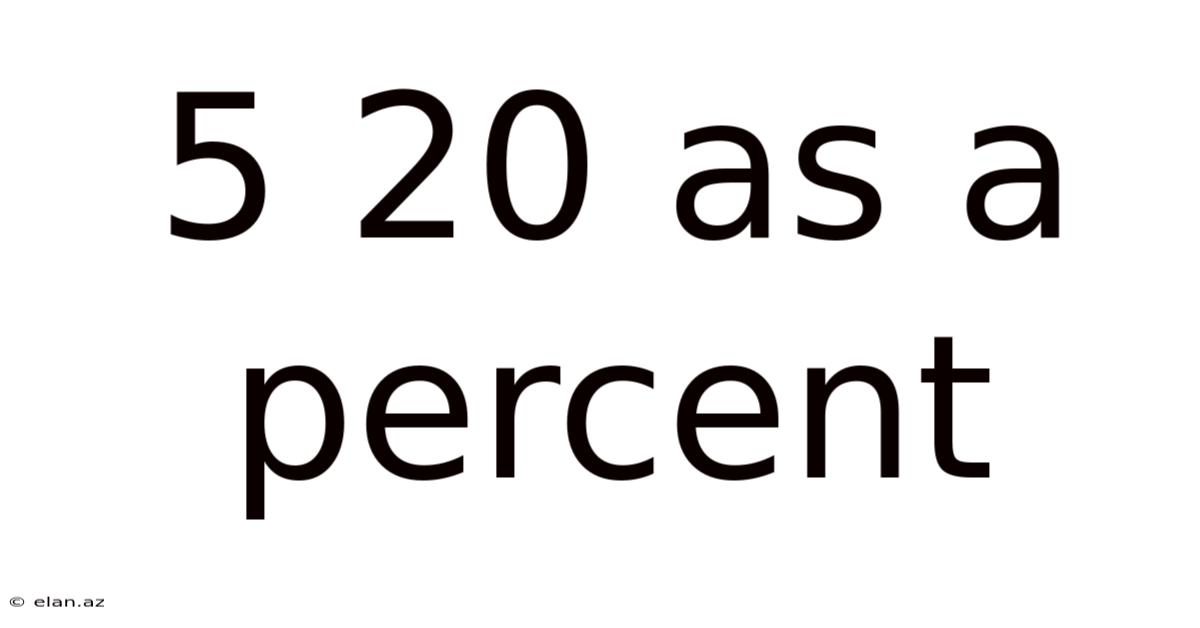
Table of Contents
Decoding 5/20 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This article delves into the conversion of the fraction 5/20 into a percentage, providing a detailed explanation suitable for learners of all levels. We will explore the process step-by-step, examine the underlying mathematical principles, and address frequently asked questions to ensure a thorough understanding of this concept.
Understanding Fractions and Percentages
Before we dive into converting 5/20 to a percentage, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 5/20, 5 is the numerator and 20 is the denominator. This means we have 5 parts out of a total of 20 parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It indicates how many parts out of 100 are being considered. For example, 25% means 25 parts out of 100. Converting a fraction to a percentage essentially involves expressing the fraction as an equivalent fraction with a denominator of 100.
Converting 5/20 to a Percentage: Step-by-Step Guide
There are several ways to convert the fraction 5/20 to a percentage. Here are two common methods:
Method 1: Simplifying the Fraction and then Converting
-
Simplify the Fraction: The first step involves simplifying the fraction 5/20. Both the numerator (5) and the denominator (20) are divisible by 5. Dividing both by 5, we get:
5 ÷ 5 / 20 ÷ 5 = 1/4
-
Convert the Simplified Fraction to a Percentage: To convert the simplified fraction 1/4 to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by 25:
(1 × 25) / (4 × 25) = 25/100
-
Express as a Percentage: Since 25/100 represents 25 parts out of 100, this is equivalent to 25%.
Therefore, 5/20 is equal to 25%.
Method 2: Direct Conversion using Division
-
Convert the Fraction to a Decimal: This method involves dividing the numerator by the denominator:
5 ÷ 20 = 0.25
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.25 × 100 = 25%
Therefore, 5/20 is equal to 25%.
Mathematical Explanation: Proportions and Ratios
The conversion of fractions to percentages relies on the fundamental mathematical concepts of proportions and ratios. A proportion is a statement that two ratios are equal. In the case of converting 5/20 to a percentage, we are essentially setting up a proportion:
5/20 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we can cross-multiply:
20x = 500
x = 500 ÷ 20
x = 25
This confirms that 5/20 is equivalent to 25%.
Real-World Applications of Percentage Calculations
Understanding how to convert fractions to percentages is crucial in various real-world scenarios:
-
Calculating Discounts: If a store offers a 25% discount on an item, and the original price is $100, you can easily calculate the discount amount ($25) and the final price ($75) by applying the percentage directly.
-
Determining Tax Amounts: Sales tax is often expressed as a percentage. Knowing how to calculate percentages helps determine the total cost of a purchase including taxes.
-
Analyzing Financial Statements: Financial reports use percentages extensively to represent various financial ratios, like profit margins, debt-to-equity ratios, and return on investment (ROI). Understanding percentages enables informed financial decision-making.
-
Interpreting Statistical Data: Percentages are commonly used to represent proportions in surveys, polls, and other statistical data. For example, a survey may show that 25% of respondents prefer a certain brand.
-
Understanding Grades and Scores: Academic grades and test scores are often expressed as percentages, reflecting the proportion of correct answers or the overall performance against the total possible score.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, absolutely! Any fraction can be converted to a percentage by dividing the numerator by the denominator and then multiplying the result by 100.
Q2: What if the fraction is an improper fraction (numerator > denominator)?
A2: Even with improper fractions, the process remains the same. Divide the numerator by the denominator, multiply by 100, and add the percentage symbol. The resulting percentage will be greater than 100%.
Q3: Is there a quick way to convert common fractions to percentages?
A3: Yes, memorizing the percentage equivalents of some common fractions (like 1/2 = 50%, 1/4 = 25%, 1/5 = 20%, etc.) can speed up the conversion process.
Q4: Why is understanding percentages important?
A4: Percentages provide a standardized way to compare proportions and make them easier to understand. They are universally used across many fields, making it a crucial skill for daily life and professional applications.
Q5: Are there any online tools or calculators for converting fractions to percentages?
A5: While many online tools can perform this conversion, understanding the underlying mathematical principles is more valuable in the long run, promoting better comprehension and problem-solving capabilities. The methods described above will equip you to handle such conversions independently.
Conclusion
Converting 5/20 to a percentage, resulting in 25%, is a simple yet fundamental mathematical operation with broad real-world applications. Understanding this conversion, along with the underlying principles of fractions, ratios, and proportions, provides a strong foundation for tackling more complex mathematical problems and confidently interpreting numerical data presented in percentage form. This skill is essential for success in various fields, from finance and statistics to everyday life situations. The methods discussed above offer multiple approaches, allowing you to choose the one that best suits your understanding and preferences. Remember, practice makes perfect! The more you work with fractions and percentages, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
Bohr Effect A Level Biology
Sep 20, 2025
-
Bus Network Advantages And Disadvantages
Sep 20, 2025
-
How The Bricks Are Made
Sep 20, 2025
-
Simultaneous Equations Answers And Questions
Sep 20, 2025
-
Spherical Coordinates To Cartesian Coordinates
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 5 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.