5 4 As A Decimal
elan
Sep 19, 2025 · 6 min read
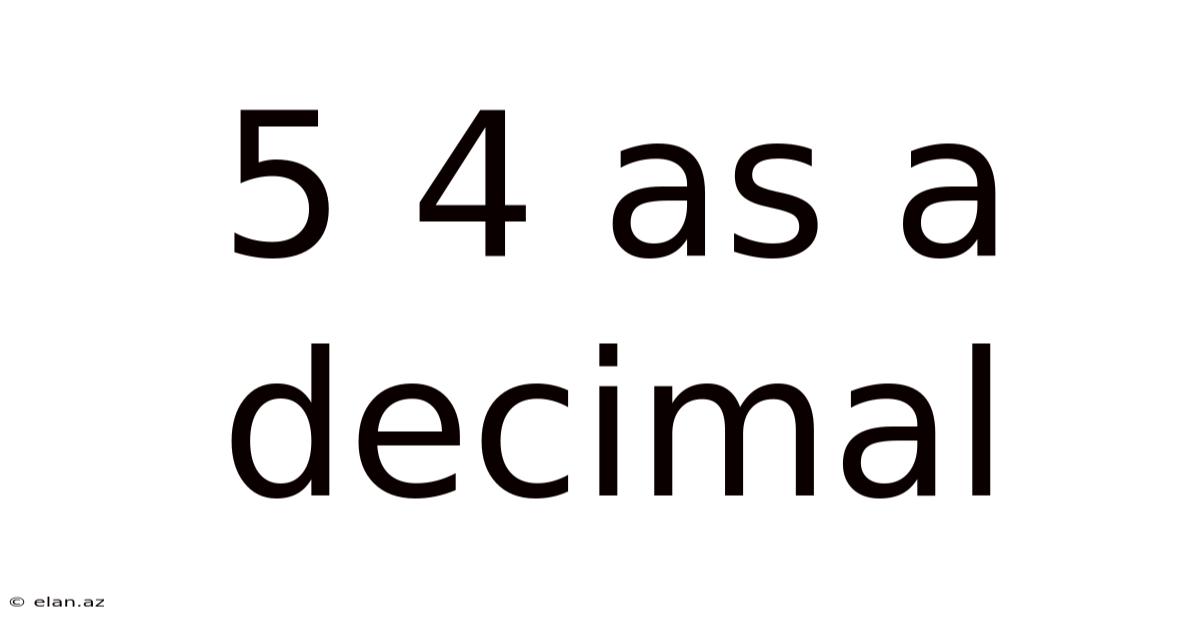
Table of Contents
Decoding 5/4 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics. This comprehensive guide delves into the conversion of the fraction 5/4 into its decimal form, exploring the underlying principles, different methods of conversion, and practical applications. We'll cover everything from the basics to more advanced concepts, making this a valuable resource for students and anyone looking to solidify their understanding of fractions and decimals. This guide will also explore related concepts and answer frequently asked questions, ensuring a complete understanding of this seemingly simple yet crucial mathematical concept.
Introduction: Understanding Fractions and Decimals
Before we jump into converting 5/4, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 5/4, 5 is the numerator and 4 is the denominator. This indicates that we have 5 parts out of a total of 4 parts.
A decimal is another way to represent a part of a whole, using the base-10 number system. Decimals use a decimal point to separate the whole number part from the fractional part. For example, 2.5 represents two whole units and five-tenths of a unit.
Converting between fractions and decimals is a crucial skill in mathematics, allowing us to represent the same value in different formats, each suitable for different calculations and contexts.
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is through long division. We divide the numerator (5) by the denominator (4).
-
Set up the long division: Write 5 inside the division symbol and 4 outside.
-
Divide: 4 goes into 5 one time (4 x 1 = 4). Write 1 above the 5.
-
Subtract: Subtract 4 from 5, leaving 1.
-
Bring down the decimal point and add a zero: Add a decimal point after the 1 in the quotient (the answer) and add a zero to the remainder (1). This doesn't change the value of the number; we're essentially adding 10 tenths.
-
Continue dividing: 4 goes into 10 two times (4 x 2 = 8). Write 2 after the decimal point in the quotient.
-
Subtract again: Subtract 8 from 10, leaving 2.
-
Repeat: Add another zero to the remainder. 4 goes into 20 five times (4 x 5 = 20). Write 5 after the 2 in the quotient.
-
Final result: The remainder is now 0, indicating that the division is complete. The decimal equivalent of 5/4 is 1.25.
Method 2: Using Equivalent Fractions
Another approach involves converting the improper fraction 5/4 into a mixed number, and then converting the fractional part to a decimal.
-
Convert to a mixed number: Since the numerator (5) is larger than the denominator (4), we have an improper fraction. We divide 5 by 4: 5 ÷ 4 = 1 with a remainder of 1. This means 5/4 is equivalent to the mixed number 1 1/4.
-
Convert the fractional part to a decimal: The fractional part is 1/4. We know that 1/4 is equivalent to 0.25 (a quarter).
-
Combine: Add the whole number part (1) and the decimal part (0.25) to get 1.25.
Method 3: Understanding Place Value
This method emphasizes the underlying principles of the decimal system. The fraction 5/4 represents 5 divided into 4 equal parts. We can think of this as 4/4 + 1/4. 4/4 is equal to 1 (one whole). 1/4 represents one part out of four equal parts.
Since a decimal represents parts of a whole based on powers of 10, we need to express 1/4 as a decimal fraction. We can consider place values: tenths, hundredths, thousandths, and so on. We know that 1/4 is equivalent to 25/100, which is written as 0.25 in decimal form. Therefore, 5/4 = 1 + 0.25 = 1.25.
The Significance of 5/4 and its Decimal Equivalent (1.25)
The fraction 5/4 and its decimal equivalent, 1.25, are frequently encountered in various mathematical and real-world applications. Understanding their relationship is crucial for several reasons:
-
Percentage Calculations: 1.25 can be easily converted to a percentage by multiplying by 100, resulting in 125%. This is useful in various applications, including finance, statistics, and everyday life.
-
Measurement and Scaling: In scenarios involving measurements (length, weight, volume), 1.25 might represent a quantity exceeding the base unit. For example, 1.25 meters would represent 1 meter and 25 centimeters.
-
Ratio and Proportion Problems: The concept of ratios and proportions is often expressed using fractions. Understanding decimal equivalents is key to solving these problems efficiently.
-
Data Analysis: In data analysis, it's often necessary to convert fractions to decimals for calculations and representation in graphs and charts.
Further Exploration: Working with Decimals
Once you have a firm grasp on converting fractions to decimals, you can extend your knowledge to work with more complex decimal numbers and operations:
-
Rounding Decimals: Often, you might need to round decimals to a specific number of decimal places for simplicity or accuracy. For example, 1.25 rounded to one decimal place would remain 1.3.
-
Decimal Addition, Subtraction, Multiplication, and Division: Performing these arithmetic operations with decimals involves understanding place value and aligning decimal points correctly.
-
Converting Decimals to Fractions: Conversely, it's also essential to be able to convert decimals back to fractions. This involves understanding place values and simplifying the resulting fraction.
Frequently Asked Questions (FAQs)
Q1: Is there a quicker way to convert 5/4 to a decimal besides long division?
A1: Yes, recognizing that 1/4 = 0.25 provides a shortcut. Since 5/4 = 1 1/4, you can directly add 1 + 0.25 = 1.25.
Q2: What if the fraction had a larger denominator? Would the long division method still be the best approach?
A2: While long division works for all fractions, for fractions with larger denominators, using a calculator might be more efficient.
Q3: Why is understanding the conversion between fractions and decimals important?
A3: It’s crucial for seamlessly moving between different mathematical representations, allowing for easier calculations and problem-solving in various fields.
Q4: Can all fractions be converted to terminating decimals (decimals that end)?
A4: No. Fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals (decimals that have a pattern that repeats indefinitely).
Conclusion: Mastering Fractions and Decimals
Converting 5/4 to its decimal equivalent, 1.25, provides a foundational understanding of the relationship between fractions and decimals. Mastering this conversion not only strengthens your mathematical skills but also enhances your ability to tackle more complex mathematical problems and real-world scenarios involving measurements, proportions, and data analysis. Remember to practice the different methods outlined in this guide and explore additional resources to further solidify your understanding of this important mathematical concept. By understanding these fundamental concepts, you'll build a strong base for more advanced mathematical studies.
Latest Posts
Latest Posts
-
A Level Chemistry Atomic Structure
Sep 19, 2025
-
To Some Degree Crossword Clue
Sep 19, 2025
-
Mig Welding Advantages And Disadvantages
Sep 19, 2025
-
Structure And Bonding Of Diamond
Sep 19, 2025
-
How Long Is Twenty Feet
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 4 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.