5 Divided By 5 3
elan
Sep 20, 2025 · 5 min read
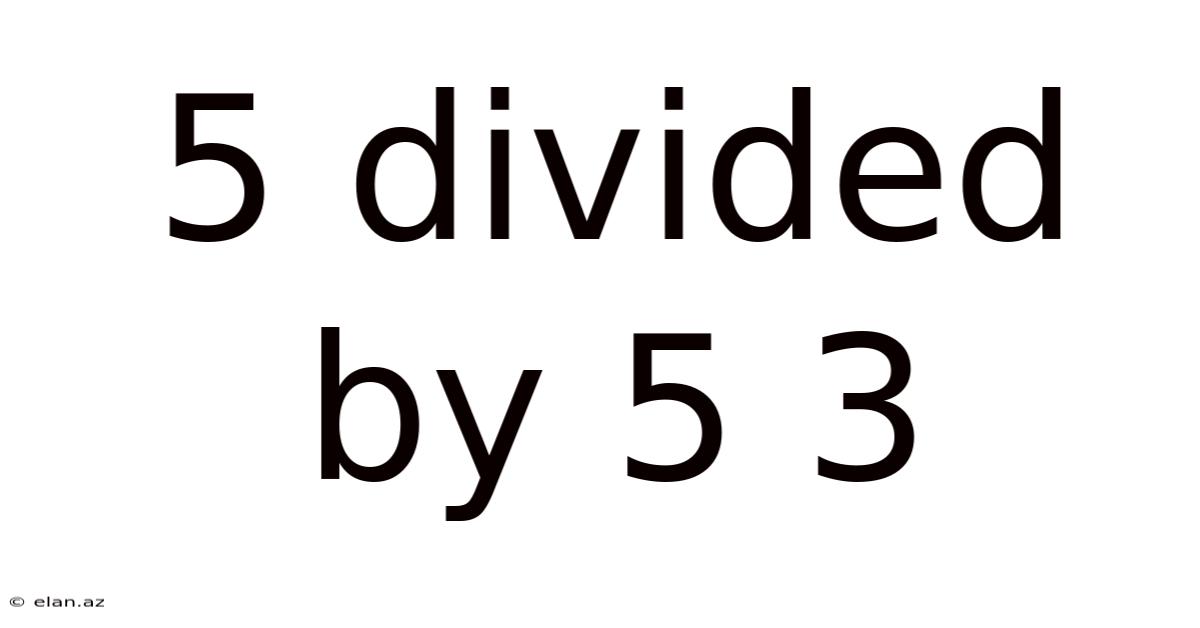
Table of Contents
Decoding 5 Divided by 5⅓: A Deep Dive into Fraction Division
This article explores the seemingly simple yet surprisingly nuanced problem of dividing 5 by the mixed number 5⅓. We'll break down the process step-by-step, explaining the underlying mathematical principles, and addressing common misconceptions. Understanding this seemingly basic calculation offers a gateway to mastering more complex fraction operations. By the end, you'll not only know the answer but also understand why the answer is what it is.
Introduction: Understanding the Problem
The question, "What is 5 divided by 5⅓?", presents a common challenge in arithmetic. Many find fraction division daunting, but with a systematic approach, it becomes manageable. The key lies in understanding the fundamental principles of fraction manipulation and applying them logically. We'll approach this problem by converting the mixed number into an improper fraction and then applying the rules of fraction division. This approach provides a solid foundation for tackling similar problems. We will also explore the concepts of reciprocals and their crucial role in simplifying the division process.
Step-by-Step Solution: Converting and Dividing
-
Converting the Mixed Number: The first step involves transforming the mixed number 5⅓ into an improper fraction. A mixed number consists of a whole number and a fraction. To convert it, we multiply the whole number (5) by the denominator of the fraction (3), add the numerator (1), and keep the same denominator. This gives us:
5⅓ = (5 * 3 + 1) / 3 = 16/3
-
Rewriting the Division Problem: Now, our problem is rewritten as: 5 ÷ (16/3)
-
Reciprocals: The Key to Fraction Division: Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. The reciprocal of 16/3 is 3/16.
-
Converting the Whole Number to a Fraction: To proceed smoothly, let's convert the whole number 5 into a fraction. Any whole number can be expressed as a fraction with a denominator of 1. Thus, 5 becomes 5/1.
-
Multiplying Fractions: Now, our problem becomes: (5/1) * (3/16)
-
Multiplying Numerators and Denominators: We multiply the numerators together and the denominators together separately.
(5 * 3) / (1 * 16) = 15/16
Therefore, 5 divided by 5⅓ is equal to 15/16.
Explanation of the Mathematical Principles
The process we've followed relies on a few core mathematical principles:
-
Mixed Number Conversion: Converting mixed numbers to improper fractions is essential for efficient calculations. It streamlines the process and avoids confusion caused by working with both whole numbers and fractions simultaneously.
-
Fraction Division as Multiplication by the Reciprocal: This is a fundamental rule of fraction arithmetic. Dividing by a fraction is the same as multiplying by its inverse (reciprocal). This simplifies the calculation significantly, making it easier to manage.
-
Multiplication of Fractions: The straightforward multiplication of numerators and denominators ensures that the result accurately reflects the original division problem.
Visual Representation: Understanding the Division
Imagine you have 5 pizzas, and you want to divide them equally among groups, each of which receives 5⅓ pizzas. How many groups can you create?
The answer, 15/16, might seem counterintuitive initially. It implies that you can create a little less than one full group. This is because the size of each group (5⅓ pizzas) is larger than the total number of pizzas you have (5).
The fraction 15/16 represents a portion of a group. It means you could almost create a whole group, but you fall slightly short.
Addressing Common Misconceptions
A common mistake is to simply divide the whole numbers (5 ÷ 5 = 1) and ignore the fractional part. This approach is incorrect because it fails to account for the fractional component of the divisor (5⅓). Remember, the entire value of the divisor (5⅓) must be considered in the division process.
Another misconception is to incorrectly invert only the fractional part of the mixed number (inverting only ⅓ to 3) instead of converting the entire mixed number to an improper fraction and then inverting. This leads to an inaccurate result.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator for this problem?
A: Yes, most calculators can handle fraction division directly. However, understanding the underlying mathematical principles is crucial for building a strong foundation in arithmetic.
-
Q: What if the divisor was a smaller fraction, say ⅓?
A: In that case, the answer would be larger than 5. The division would result in 15 (5 x 3). The size of the result depends directly on the size of the divisor; a smaller divisor leads to a larger quotient.
-
Q: Is there another way to solve this problem?
A: While the method described above is the most efficient, you could also use decimal approximations. Convert both numbers into decimals (5 and 5.333...), then perform the division. However, this approach might introduce rounding errors, leading to a slightly less accurate result than using fractions.
Conclusion: Mastering Fraction Division
Mastering fraction division is a fundamental skill in mathematics. Understanding the concept of reciprocals and the proper method for converting mixed numbers to improper fractions are key to solving these types of problems accurately and efficiently. This article has provided a detailed walkthrough, explaining not just how to solve the problem but also why the solution is obtained through the specific steps employed. Practice is essential; working through similar problems will solidify your understanding and improve your proficiency in fraction arithmetic. The seemingly simple problem of 5 divided by 5⅓ demonstrates the importance of a structured and methodical approach to solving even basic mathematical equations. By understanding the principles discussed here, you can confidently approach more complex fraction problems in the future.
Latest Posts
Latest Posts
-
Words With Y In Middle
Sep 20, 2025
-
Distinguish Between Strategy And Tactics
Sep 20, 2025
-
Things That Rhyme With Laugh
Sep 20, 2025
-
Use Tolerance In A Sentence
Sep 20, 2025
-
20 Square Meters To Meters
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 5 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.