5 X 4 X 3
elan
Sep 24, 2025 · 6 min read
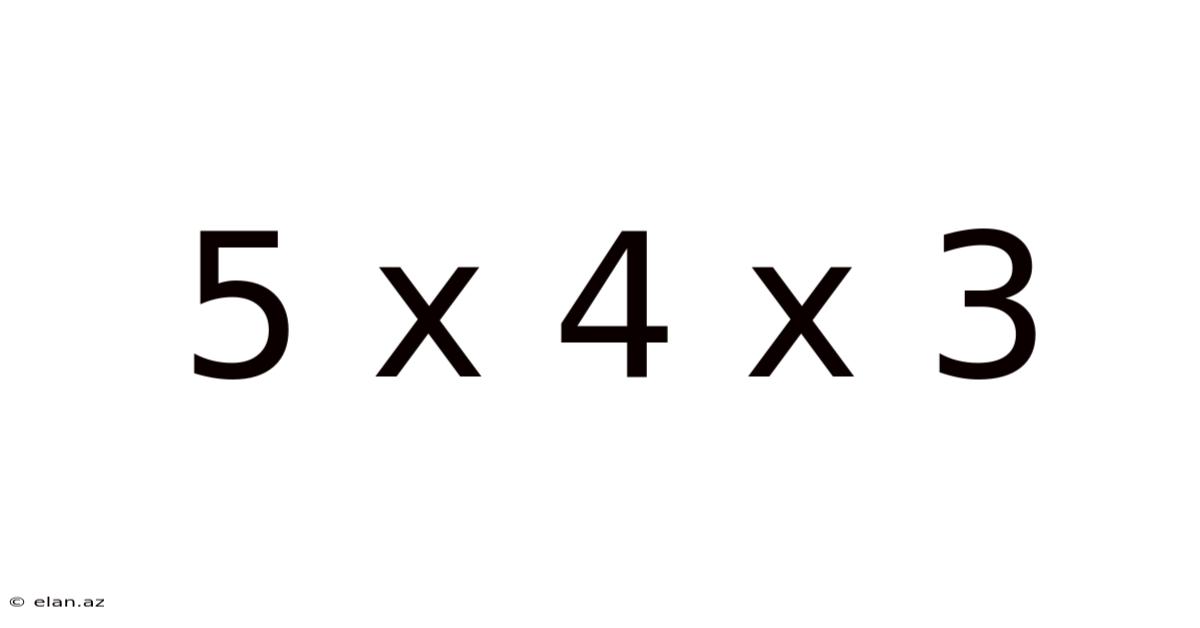
Table of Contents
Unraveling the Mystery of 5 x 4 x 3: A Deep Dive into Multiplication and its Applications
This article delves into the seemingly simple calculation of 5 x 4 x 3, exploring its mathematical underpinnings, practical applications, and broader implications within the world of mathematics and beyond. Understanding this seemingly basic equation unlocks a gateway to more complex concepts, demonstrating the power of multiplication and its foundational role in various fields. We'll examine the process, explore different methods of solving it, and then venture into the fascinating world of its applications in real-life scenarios. This comprehensive guide is designed for learners of all levels, from elementary school students solidifying their foundational knowledge to those seeking a deeper understanding of mathematical principles.
Understanding the Fundamentals: What is Multiplication?
Multiplication is a fundamental arithmetic operation that represents repeated addition. Instead of adding the same number multiple times (e.g., 5 + 5 + 5 + 5), multiplication provides a concise way to express this: 5 x 4. In our equation, 5 x 4 x 3, we're essentially performing repeated addition three times over. It's crucial to understand this underlying principle to grasp the essence of the calculation. The numbers involved – 5, 4, and 3 – are called factors, and the result of the multiplication is called the product.
Methods for Solving 5 x 4 x 3
There are several approaches to solving 5 x 4 x 3, each offering a slightly different perspective on the underlying mathematical principles:
1. Step-by-Step Multiplication: This is the most straightforward method, involving performing the multiplications sequentially.
- Step 1: Multiply 5 by 4: 5 x 4 = 20
- Step 2: Multiply the result (20) by 3: 20 x 3 = 60
Therefore, 5 x 4 x 3 = 60.
2. Commutative Property: The commutative property of multiplication states that the order of the factors does not affect the product. This means that 5 x 4 x 3 is the same as 4 x 5 x 3, 3 x 5 x 4, and so on. This property allows for flexibility in solving the equation. For instance:
- Method A: (5 x 4) x 3 = 20 x 3 = 60
- Method B: 5 x (4 x 3) = 5 x 12 = 60
Both methods yield the same result, highlighting the power of the commutative property.
3. Using Visual Aids: Visual aids, such as arrays or diagrams, can be particularly helpful for visualizing multiplication, especially for younger learners. Imagine five rows of four items each; this represents 5 x 4 = 20. Then, imagine three sets of these arrays; this would visually represent 20 x 3 = 60.
4. Mental Math: With practice, you can perform this calculation mentally. Breaking down the equation into smaller, more manageable steps can be beneficial. For example, you could think of it as (5 x 4) x 3 or 5 x (4 x 3).
The Associative Property in Action
The associative property of multiplication further clarifies the flexibility inherent in solving this equation. It states that the grouping of factors does not affect the product. This is demonstrated by the two methods shown above in the Commutative Property section. Whether we multiply 5 and 4 first, or 4 and 3 first, the final product remains 60. This property is crucial for more complex calculations involving multiple factors.
Beyond the Calculation: Exploring Applications
While the calculation itself is simple, its implications extend far beyond a basic arithmetic problem. Understanding 5 x 4 x 3 opens doors to a broader appreciation of mathematical principles and their real-world applications.
1. Everyday Calculations: Imagine you're buying packs of cookies. Each pack contains 5 cookies, and you buy 4 packs per week for 3 weeks. The total number of cookies you consume is 5 x 4 x 3 = 60 cookies. This simple example demonstrates how multiplication is crucial for everyday budgeting and purchasing decisions.
2. Geometry and Volume: Consider a rectangular prism (a box). If the prism has dimensions of 5 cm x 4 cm x 3 cm, then 5 x 4 x 3 = 60 cubic centimeters represents its volume – the amount of space it occupies. This highlights the connection between multiplication and three-dimensional shapes.
3. Combinations and Permutations: In probability and combinatorics, multiplication plays a vital role in determining the number of possible outcomes. Imagine choosing outfits: you have 5 shirts, 4 pants, and 3 pairs of shoes. The total number of different outfit combinations is 5 x 4 x 3 = 60.
4. Data Analysis and Statistics: Multiplication is fundamental in various statistical calculations, including calculating means, variances, and standard deviations – all crucial tools for analyzing data sets.
Expanding the Concept: Factorials and Beyond
The equation 5 x 4 x 3 can be viewed as a simplified version of a factorial (denoted by !). A factorial is the product of all positive integers less than or equal to a given positive integer. For example, 5! (5 factorial) is 5 x 4 x 3 x 2 x 1 = 120. Our equation is a partial factorial, omitting the factors 2 and 1. Understanding factorials opens the door to more advanced mathematical concepts in areas such as probability and calculus.
Addressing Common Misconceptions
A common misconception is that the order of operations always dictates a specific approach. While the order of operations (PEMDAS/BODMAS) is essential for equations with multiple operations (parentheses, exponents, multiplication, division, addition, subtraction), in a purely multiplicative equation like 5 x 4 x 3, the commutative and associative properties allow for flexibility in the order of calculation.
Frequently Asked Questions (FAQ)
Q: Is there only one way to solve 5 x 4 x 3?
A: No. The commutative and associative properties of multiplication allow for multiple ways to solve this equation, all leading to the same answer (60).
Q: Why is understanding this equation important?
A: This seemingly simple equation lays the groundwork for understanding more complex mathematical concepts and their applications in various fields, from everyday calculations to advanced statistical analysis.
Q: Can this equation be applied to real-world problems?
A: Yes. It can be applied to numerous scenarios involving counting, measuring, and calculating probabilities, as shown in the applications section above.
Q: What happens if we change the order of the numbers?
A: The product remains the same (60) due to the commutative property of multiplication.
Conclusion: The Significance of Simplicity
The calculation 5 x 4 x 3, while seemingly trivial, serves as a powerful illustration of fundamental mathematical principles. Its simplicity belies its importance, demonstrating the beauty and power of multiplication and its far-reaching applications. Mastering this simple calculation is not just about getting the right answer (60); it's about building a solid foundation for more complex mathematical explorations, fostering critical thinking, and developing problem-solving skills that are applicable in numerous aspects of life. By understanding this equation thoroughly, learners gain a deeper appreciation for the elegance and utility of mathematics. The journey from a simple calculation to a comprehensive understanding of its implications highlights the multifaceted nature of mathematics and its profound influence on our world.
Latest Posts
Latest Posts
-
Cubed And Squared Numbers Worksheet
Sep 24, 2025
-
Quiz Questions Science With Answers
Sep 24, 2025
-
What Is 20 Of 25000
Sep 24, 2025
-
Free From Danger Crossword Clue
Sep 24, 2025
-
Taylor Expansion For Two Variables
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 5 X 4 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.