50 60 As A Percentage
elan
Sep 21, 2025 · 5 min read
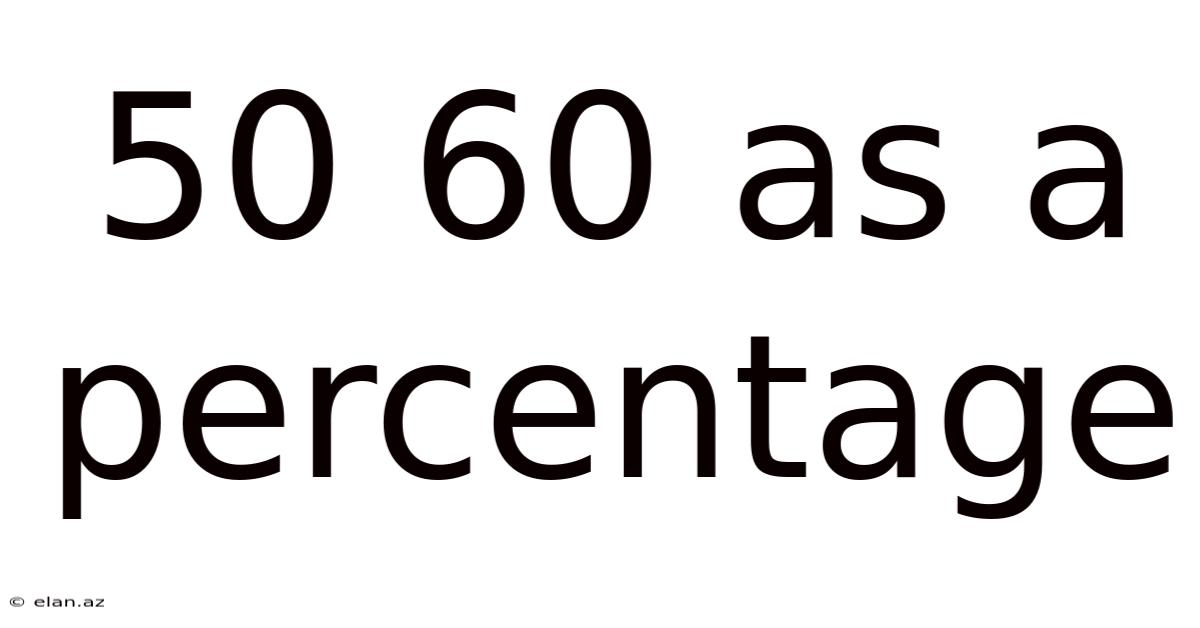
Table of Contents
Decoding 50/60 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with applications spanning various fields, from calculating discounts and taxes to analyzing data and understanding statistics. This article will thoroughly explore how to convert the fraction 50/60 into a percentage, delving into the underlying concepts and providing practical examples. We'll also address common misconceptions and offer additional tips for mastering percentage calculations. By the end, you'll not only know the answer but also understand the process deeply, equipping you to tackle similar problems with confidence.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, or 50/100. Converting a fraction like 50/60 into a percentage involves expressing it in this "per hundred" format. This seemingly simple task is crucial for various applications, including:
- Financial calculations: Interest rates, discounts, tax calculations, and profit margins are all expressed as percentages.
- Data analysis: Percentages are essential for representing proportions, trends, and comparisons in data sets.
- Scientific measurements: Percentages are used in many scientific fields to represent concentrations, efficiencies, and error margins.
- Everyday life: We encounter percentages constantly, from sale signs in stores to statistics in news reports.
Converting 50/60 to a Percentage: Step-by-Step Guide
The conversion of 50/60 to a percentage involves a straightforward two-step process:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
50 ÷ 60 = 0.8333...
The result is a recurring decimal, meaning the digits "3" repeat infinitely. For practical purposes, we'll round this to a reasonable number of decimal places, such as 0.833.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.833 x 100 = 83.3%
Therefore, 50/60 is approximately 83.3%.
Simplifying the Fraction (Optional but Recommended)
Before performing the division, it's often beneficial to simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 50 and 60 is 10. Dividing both the numerator and denominator by 10 simplifies the fraction:
50 ÷ 10 = 5 60 ÷ 10 = 6
This simplifies the fraction to 5/6. Now, performing the division:
5 ÷ 6 ≈ 0.833
Multiplying by 100 gives us the same result: 83.3%. Simplifying the fraction first makes the division easier and reduces the risk of errors, especially when dealing with larger numbers.
Understanding the Result: What Does 83.3% Mean?
The result, 83.3%, signifies that 50 represents 83.3% of 60. In other words, if you had a group of 60 items, 50 of them would constitute 83.3% of the total.
Alternative Methods for Percentage Calculation
While the method outlined above is the most straightforward, there are other approaches to convert fractions to percentages:
- Using Proportions: You can set up a proportion: 50/60 = x/100, where 'x' represents the percentage. Solving for 'x' will give you the percentage.
- Using a Calculator: Most calculators have a percentage function that directly converts fractions or decimals to percentages. Simply input the fraction 50/60 and press the percentage button.
Further Exploration: Working with Percentages
Mastering percentage calculations involves understanding various related operations:
- Finding a percentage of a number: To find, say, 20% of 150, multiply 150 by 0.20 (which is the decimal equivalent of 20%).
- Finding the percentage increase or decrease: Calculate the difference between two numbers, divide the difference by the original number, and multiply by 100 to express the change as a percentage.
- Working with percentage changes: Understanding how percentages compound over time is essential in finance and investment.
Practical Applications and Real-World Examples
Let's illustrate the practical application of converting fractions to percentages:
- Test Scores: If you answered 50 out of 60 questions correctly on a test, your score is 83.3%.
- Sales: A store offers a discount of 50 out of 60 dollars on a particular item. This represents an 83.3% discount.
- Surveys: If 50 out of 60 respondents in a survey answered "yes" to a question, 83.3% responded affirmatively.
Common Misconceptions about Percentages
A frequent mistake is confusing percentages with fractions. While closely related, they are not interchangeable in every context. A percentage always represents a fraction of 100, whereas a fraction can represent any ratio.
Another common error is incorrectly calculating percentage increases or decreases. Always remember to base the calculation on the original value.
Frequently Asked Questions (FAQ)
-
Q: What if I get a recurring decimal when converting a fraction to a percentage?
- A: Round the decimal to an appropriate number of decimal places for practical purposes. The level of precision required will depend on the context.
-
Q: Can I convert any fraction to a percentage?
- A: Yes, any fraction can be converted to a percentage by dividing the numerator by the denominator and multiplying by 100.
-
Q: Are there any online tools or calculators that can help me with percentage calculations?
- A: Yes, many online calculators and tools can perform percentage calculations.
Conclusion: Mastering the Art of Percentages
Understanding how to convert fractions to percentages is a valuable skill with broad applications. The process is straightforward: convert the fraction to a decimal by dividing the numerator by the denominator, and then multiply the decimal by 100 to obtain the percentage. Remember to simplify fractions when possible to make the calculation easier. By mastering these techniques and understanding the underlying concepts, you'll confidently tackle percentage calculations in various contexts, whether it's managing your finances, analyzing data, or simply understanding the world around you. Practice is key – the more you work with percentages, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
Modulus Of Elasticity Of Steel
Sep 21, 2025
-
Difference Between Bond And Loan
Sep 21, 2025
-
5 Letter Word Ending Th
Sep 21, 2025
-
Life Cycle Of A Human
Sep 21, 2025
-
How Many Inches Is 23cm
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 50 60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.