6 25 As A Percentage
elan
Sep 12, 2025 · 5 min read
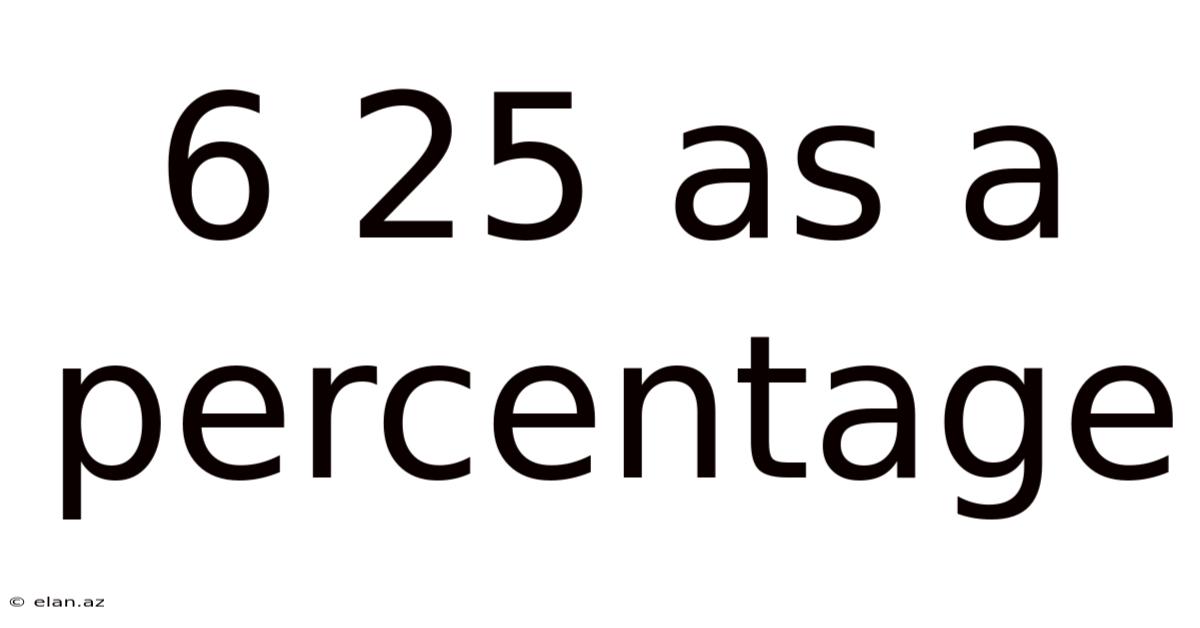
Table of Contents
Understanding 6/25 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from calculating discounts in shopping to understanding financial reports. This article provides a comprehensive guide to understanding how to convert the fraction 6/25 into a percentage, explaining the process step-by-step and exploring related concepts. We'll cover different methods, delve into the underlying mathematical principles, and answer frequently asked questions. By the end, you'll not only know the answer but also possess a solid understanding of percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 6/25, 6 is the numerator and 25 is the denominator. This means we have 6 parts out of a total of 25 parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion or rate per hundred. For instance, 25% means 25 out of 100, which can also be written as the fraction 25/100. Converting fractions to percentages involves finding the equivalent fraction with a denominator of 100.
Method 1: Converting the Fraction to an Equivalent Fraction with a Denominator of 100
This is the most straightforward method for converting 6/25 to a percentage. The goal is to find an equivalent fraction where the denominator is 100. To achieve this, we need to determine what number, when multiplied by 25, equals 100. This number is 4 (25 x 4 = 100). Since we multiply the denominator by 4, we must also multiply the numerator by 4 to maintain the equivalence of the fraction:
6/25 = (6 x 4) / (25 x 4) = 24/100
Now that we have an equivalent fraction with a denominator of 100, we can easily express it as a percentage: 24/100 = 24%.
Therefore, 6/25 is equal to 24%.
Method 2: Converting the Fraction to a Decimal and then to a Percentage
Another common method involves first converting the fraction to a decimal and then multiplying by 100 to obtain the percentage. To convert 6/25 to a decimal, we divide the numerator (6) by the denominator (25):
6 ÷ 25 = 0.24
Now, to convert this decimal to a percentage, we multiply by 100:
0.24 x 100 = 24%
This confirms that 6/25 is indeed equal to 24%. This method is particularly useful when dealing with fractions that are not easily converted to equivalent fractions with a denominator of 100.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We can set up a proportion where the fraction 6/25 is equal to x/100, where x represents the percentage we're trying to find:
6/25 = x/100
To solve for x, we cross-multiply:
25x = 600
Now, divide both sides by 25:
x = 600 ÷ 25 = 24
Therefore, x = 24, meaning 6/25 is equal to 24%. This method reinforces the underlying mathematical relationship between fractions and percentages.
The Mathematical Principle Behind Percentage Conversions
The core principle behind converting fractions to percentages is the concept of proportionality. A percentage is simply a fraction expressed as a rate per hundred. The process involves finding an equivalent fraction with a denominator of 100, which directly represents the percentage. Whether you use the method of finding an equivalent fraction, converting to a decimal, or using proportions, the underlying principle remains the same: maintaining the proportionality of the original fraction.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in numerous real-world applications. Here are a few examples:
- Financial Calculations: Calculating interest rates, discounts, tax rates, profit margins, and more all involve working with percentages.
- Data Analysis: Percentages are frequently used to represent proportions in data sets, such as market share, survey results, and statistical analyses.
- Everyday Life: Calculating tips in restaurants, understanding sale discounts in stores, and interpreting statistics in news reports all require an understanding of percentages.
- Scientific Calculations: Percentages are used extensively in scientific fields to represent concentrations, error margins, and other quantitative relationships.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to convert fractions to percentages?
A1: Yes, most calculators have the functionality to perform this conversion. You can either divide the numerator by the denominator to get the decimal and then multiply by 100, or some calculators directly allow you to input the fraction and convert it to a percentage.
Q2: What if the fraction results in a repeating decimal when converting to a percentage?
A2: If the fraction results in a repeating decimal, you can either round the decimal to a certain number of decimal places or express the percentage using the repeating decimal notation (e.g., 33.333...). The level of precision required will depend on the context of the problem.
Q3: Is there a difference between saying "24 percent" and "24 per cent"?
A3: While both are correct and understood, "percent" (one word) is the preferred and more common usage in modern English. "Per cent" (two words) is an older form that is less frequently used.
Q4: How can I improve my understanding of percentage calculations?
A4: Practice is key! Try converting different fractions to percentages using the various methods described above. You can also find online quizzes and worksheets to further strengthen your skills. Understanding the underlying mathematical principles will also help you approach more complex percentage problems confidently.
Conclusion
Converting the fraction 6/25 to a percentage is a straightforward process that can be approached through several methods. Whether you choose to find an equivalent fraction with a denominator of 100, convert to a decimal and then multiply by 100, or use proportions, the result remains the same: 24%. Understanding these different methods provides a deeper understanding of the underlying mathematical principles involved and equips you with the skills to tackle various percentage-related problems across different disciplines. Remember to practice regularly to build confidence and proficiency in this essential mathematical skill. By mastering this fundamental concept, you'll be better equipped to navigate numerical challenges in various aspects of your life and studies.
Latest Posts
Latest Posts
-
Assumptions Kinetic Theory Of Gases
Sep 12, 2025
-
Sq Mtr To Sq Yard
Sep 12, 2025
-
Games That Start With K
Sep 12, 2025
-
Exceptional Early Development Crossword Clue
Sep 12, 2025
-
Items That Start With V
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 6 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.