6 5 As A Percentage
elan
Sep 13, 2025 · 5 min read
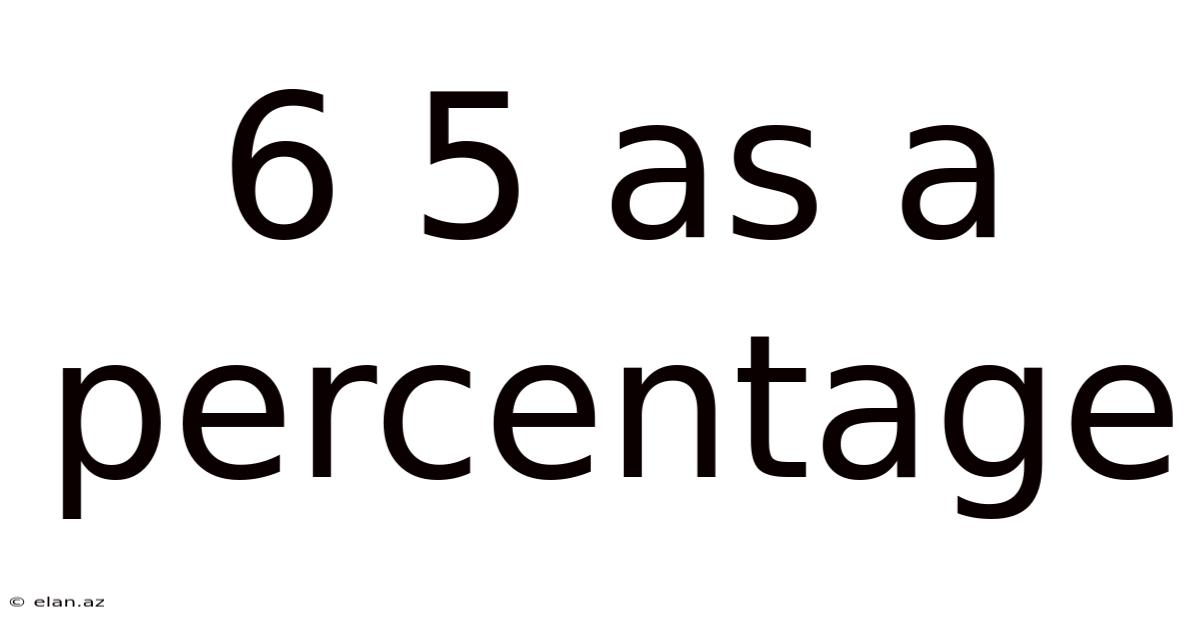
Table of Contents
Understanding 6/5 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will delve into the process of converting the fraction 6/5 into a percentage, explaining the underlying concepts and providing practical examples. We'll explore the meaning of percentages, different methods for the conversion, and address frequently asked questions. This detailed explanation aims to not only provide the answer but also equip you with a deeper understanding of the mathematical principles involved.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Percentages are used extensively to represent proportions, ratios, and changes in quantities. They offer a standardized way to compare different values and make complex data more accessible and understandable.
Converting Fractions to Percentages: The General Approach
The conversion of any fraction to a percentage involves two key steps:
- Convert the fraction to a decimal: Divide the numerator (the top number) by the denominator (the bottom number).
- Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
Let's apply this general approach to the specific fraction 6/5.
Calculating 6/5 as a Percentage: Step-by-Step
Step 1: Convert the fraction to a decimal.
To convert 6/5 to a decimal, we perform the division: 6 ÷ 5 = 1.2
Step 2: Convert the decimal to a percentage.
To convert the decimal 1.2 to a percentage, we multiply by 100: 1.2 x 100 = 120
Therefore, 6/5 as a percentage is 120%.
Understanding the Result: What does 120% mean?
The result of 120% signifies that 6/5 represents a quantity that is 120% of the whole. In other words, it's 20% more than the whole. This is because 6/5 is an improper fraction, where the numerator is larger than the denominator. Improper fractions, when converted to percentages, will always result in percentages greater than 100%. This indicates a quantity exceeding the reference point (100%).
Alternative Methods for Conversion
While the above method is the most straightforward, other methods can be employed to arrive at the same result.
Method 1: Finding an Equivalent Fraction with a Denominator of 100
We can convert 6/5 to an equivalent fraction with a denominator of 100. To do this, we need to find a number that, when multiplied by 5, results in 100. That number is 20 (5 x 20 = 100). We must multiply both the numerator and the denominator by 20 to maintain the fraction's value:
(6 x 20) / (5 x 20) = 120/100
Since a percentage is a fraction out of 100, 120/100 directly translates to 120%.
Method 2: Using Proportions
We can set up a proportion to solve for the percentage:
6/5 = x/100
To solve for 'x', we cross-multiply:
5x = 600
x = 600/5 = 120
Therefore, x = 120, meaning 6/5 is equal to 120%.
Practical Applications of 6/5 as a Percentage
Understanding 120% has numerous practical applications. Consider these scenarios:
- Price Increases: If a product's price increases by 20%, the new price is 120% of the original price. If the original price was $5, the new price would be $6 ($5 x 1.2 = $6).
- Growth Rates: If a population or investment grows by 20%, the final size is 120% of the initial size.
- Performance Metrics: In certain performance metrics, exceeding expectations might be represented as a percentage greater than 100%. For example, if a sales target was 5 units and an employee sold 6 units, their performance would be 120% of the target.
Scientific and Engineering Applications
Beyond everyday calculations, understanding fractions and percentages like 6/5 (120%) is fundamental in scientific and engineering fields. For example:
- Scaling and Ratios: In engineering design, scaling a model up or down often involves using ratios and percentages. A 20% increase in scale translates to a size that's 120% of the original.
- Data Analysis: Interpreting experimental data, especially in scenarios involving growth or change, necessitates the understanding and application of percentages.
Frequently Asked Questions (FAQ)
Q1: Can a percentage be greater than 100%?
Yes, absolutely. A percentage greater than 100% indicates a quantity that exceeds the reference point (100%). This often represents growth, increase, or exceeding a target value.
Q2: What is the difference between 6/5 and 5/6 as percentages?
6/5 is 120%, while 5/6 is approximately 83.33%. The difference arises from the fact that 6/5 is an improper fraction (greater than 1), while 5/6 is a proper fraction (less than 1).
Q3: How can I easily convert fractions to percentages without a calculator?
For simpler fractions, try to find an equivalent fraction with a denominator of 100. For more complex fractions, you might need to perform long division to convert to a decimal and then multiply by 100. Memorizing common fraction-to-decimal conversions can also be helpful.
Q4: Why are percentages so important?
Percentages provide a standardized and easily understandable way to represent proportions, ratios, and changes in quantities. They facilitate comparisons across different values and simplify the interpretation of complex data, making them essential in many fields.
Conclusion
Converting 6/5 to a percentage results in 120%. This seemingly simple calculation underlines a fundamental concept in mathematics with far-reaching applications in everyday life, various professions, and scientific endeavors. Understanding the process, the meaning of the result, and the alternative methods enhances not just mathematical proficiency but also the ability to interpret and apply numerical information effectively. This comprehensive guide has aimed to illuminate the concept of percentages, especially in relation to improper fractions, providing you with the knowledge and skills to tackle similar conversions confidently and efficiently. Remember, mastering percentages isn’t just about finding the answer; it’s about understanding the why behind the calculation.
Latest Posts
Latest Posts
-
4 Letter Words From Ensure
Sep 13, 2025
-
Sigma Bonds And Pi Bonds
Sep 13, 2025
-
What Does Gmt Stand For
Sep 13, 2025
-
Good Words Starting With K
Sep 13, 2025
-
What Is The Partnership Deed
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 6 5 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.