6 Divided By 3 5
elan
Sep 23, 2025 · 5 min read
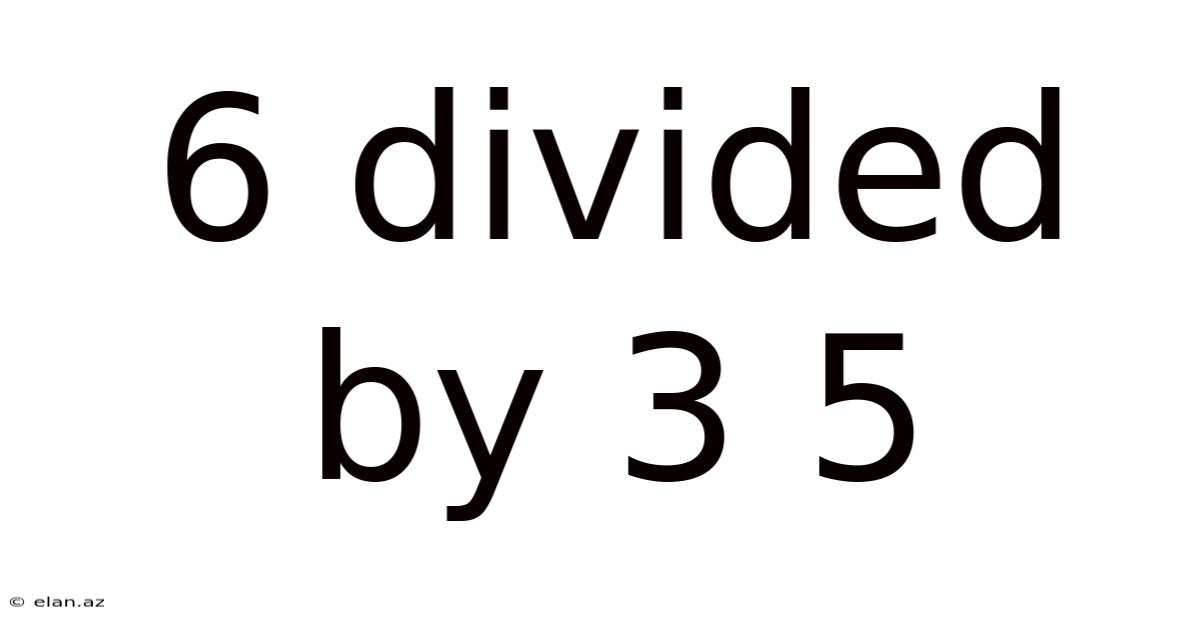
Table of Contents
Decoding 6 Divided by 3.5: A Deep Dive into Division and Decimal Arithmetic
This article explores the seemingly simple calculation of 6 divided by 3.5, delving beyond the immediate answer to understand the underlying principles of division, working with decimals, and the various methods for solving this type of problem. We'll examine different approaches, from long division to using fractions, ensuring a comprehensive understanding suitable for learners of all levels. This exploration will not only provide the solution but also build a solid foundation in mathematical reasoning.
Understanding Division
At its core, division is the inverse operation of multiplication. When we say "6 divided by 3.5," we're asking: "How many times does 3.5 fit into 6?" This question can be approached in several ways, each illuminating different aspects of the mathematical process. Understanding the concept of division is crucial before tackling the specifics of 6 ÷ 3.5.
Imagine you have 6 cookies, and you want to share them equally among 3.5 friends. This immediately highlights a challenge: you can't have half a friend! This scenario demonstrates that division involving decimals often leads to decimal answers, requiring a slightly different approach than dividing whole numbers.
Method 1: Long Division
Long division is a classic method that provides a step-by-step solution to division problems, especially those involving decimals. Here's how to solve 6 ÷ 3.5 using long division:
-
Convert to an equivalent problem without decimals: Multiply both the dividend (6) and the divisor (3.5) by 10 to remove the decimal point from the divisor. This gives us 60 ÷ 35.
-
Perform long division:
1 35 | 60 -35 25 -
Introduce the decimal point and continue: Since we have a remainder, we add a decimal point to the quotient (the answer) and a zero to the remainder.
1.714... 35 | 60.000 -35 250 -245 50 -35 150 -140 10 -
Interpret the result: The division continues indefinitely, resulting in a repeating decimal (1.714285714285...). We can round the answer to a desired level of accuracy. For example, rounded to two decimal places, the answer is approximately 1.71.
This method demonstrates the mechanics of division clearly, highlighting the process of repeatedly subtracting the divisor until the remainder is zero (or we reach the desired level of accuracy).
Method 2: Using Fractions
Fractions offer an alternative approach to solving division problems. We can rewrite 6 ÷ 3.5 as a fraction:
6/3.5
- Eliminate the decimal in the denominator: Multiply both the numerator and the denominator by 10:
60/35
- Simplify the fraction: Both 60 and 35 are divisible by 5:
12/7
- Convert to a decimal: Now we can perform the division 12 ÷ 7 using long division or a calculator:
12 ÷ 7 ≈ 1.7142857...
This method offers a different perspective, emphasizing the relationship between division and fractions. Simplifying the fraction before converting to a decimal often makes the calculation easier.
Method 3: Using a Calculator
The simplest method is to use a calculator. Enter "6 ÷ 3.5" and press the equals button. The calculator will directly provide the decimal approximation, usually showing a rounded result to several decimal places. While this is the quickest method, understanding the underlying mathematical processes, as demonstrated in the previous methods, is crucial for developing a stronger mathematical foundation.
Understanding the Decimal Result
The result of 6 ÷ 3.5 is a recurring decimal, approximately 1.7142857142857... This means the decimal part continues infinitely without repeating in a predictable pattern. Rounding is necessary for practical applications. The level of rounding depends on the required accuracy of the answer. For most purposes, rounding to two or three decimal places (1.71 or 1.714) is sufficient.
Real-World Applications
Division involving decimals is commonly used in various real-world situations. Consider these examples:
- Sharing resources: Dividing a quantity of something (money, food, materials) among a group of people.
- Calculating unit prices: Determining the cost per item when buying in bulk.
- Averaging data: Calculating the average of a set of measurements or scores.
- Scaling recipes: Adjusting ingredient quantities in cooking or baking.
- Engineering and design: Many engineering calculations involve decimal numbers and precise divisions.
Frequently Asked Questions (FAQ)
Q: Why does 6 divided by 3.5 result in a decimal?
A: Because 3.5 doesn't divide evenly into 6. When the divisor (3.5) doesn't divide the dividend (6) completely, the result is a decimal or fraction.
Q: What is the most accurate answer to 6 ÷ 3.5?
A: There is no single "most accurate" answer. The result is a recurring decimal (1.7142857...), which continues infinitely. The accuracy depends on the number of decimal places you round to.
Q: Can I use a calculator for this problem?
A: Yes, using a calculator is the quickest way to find an approximate decimal answer. However, it's also important to understand the methods behind the calculation.
Q: How do I choose the appropriate level of rounding?
A: The appropriate level of rounding depends on the context. For most everyday situations, rounding to two or three decimal places is sufficient. In scientific or engineering applications, higher accuracy may be necessary.
Conclusion
The calculation of 6 divided by 3.5, seemingly simple at first glance, opens a window into the broader world of decimal arithmetic and division. This exploration demonstrates the application of long division, fraction manipulation, and the use of calculators to arrive at the solution. Understanding the different approaches not only provides the answer but also builds a deeper understanding of fundamental mathematical principles, allowing you to tackle more complex problems with confidence. Remember that mastering the underlying concepts is more valuable than simply obtaining the answer. Practice different methods and explore various examples to solidify your grasp of division and decimal arithmetic.
Latest Posts
Latest Posts
-
What Is Formula For Energy
Sep 23, 2025
-
Mothers Day Poems From Daughter
Sep 23, 2025
-
Words That Start With Ya
Sep 23, 2025
-
Chemical Equations Balancing Equations Worksheet
Sep 23, 2025
-
Mixed And Improper Fractions Worksheet
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.