7 50 As A Percent
elan
Sep 18, 2025 · 5 min read
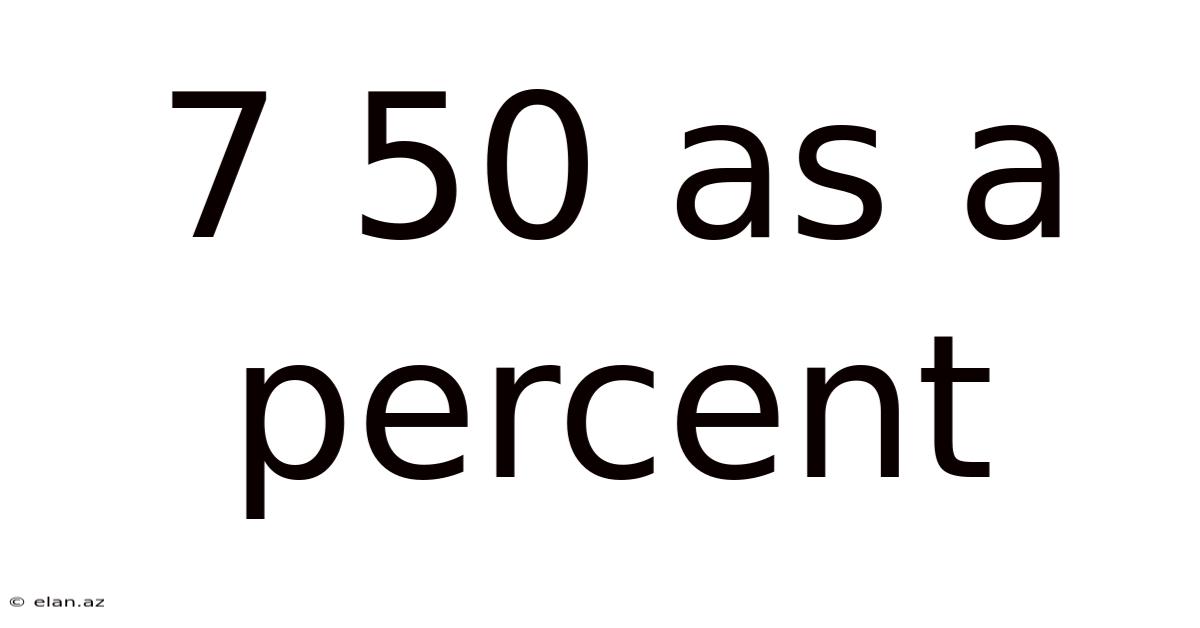
Table of Contents
7/50 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday calculations. This comprehensive guide will delve into the conversion of the fraction 7/50 into a percentage, exploring multiple methods, providing a detailed explanation of the underlying principles, and addressing common questions. We'll also examine the practical implications of this conversion and its relevance in various real-world scenarios.
Understanding Fractions and Percentages
Before we dive into converting 7/50, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts in the whole.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ( per centum in Latin). Percentages are commonly used to represent proportions, rates, or changes.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage is through division. We simply divide the numerator by the denominator and then multiply the result by 100%.
Steps:
- Divide the numerator by the denominator: 7 ÷ 50 = 0.14
- Multiply the result by 100%: 0.14 × 100% = 14%
Therefore, 7/50 is equal to 14%.
Method 2: Converting the Fraction to an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. This makes the conversion to a percentage particularly simple because a percentage is inherently a fraction out of 100.
Steps:
- Find a number that, when multiplied by the denominator (50), equals 100: This number is 2 (because 50 x 2 = 100).
- Multiply both the numerator and denominator by this number: (7 x 2) / (50 x 2) = 14/100
- Express the equivalent fraction as a percentage: 14/100 = 14%
Again, we arrive at the conclusion that 7/50 is equivalent to 14%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We set up a proportion where the fraction 7/50 is equal to x/100, where 'x' represents the percentage we're trying to find.
Steps:
- Set up the proportion: 7/50 = x/100
- Cross-multiply: 7 x 100 = 50 x x
- Solve for x: 700 = 50x => x = 700/50 = 14
Therefore, x = 14, meaning 7/50 is equal to 14%.
The Significance of 14%
Understanding that 7/50 represents 14% allows for various applications. For example:
- Financial Calculations: If a company reports a profit of 7 out of 50 units sold, this translates to a 14% profit margin. This information is crucial for assessing profitability and making informed business decisions.
- Statistical Analysis: In data analysis, 14% could represent the percentage of respondents who chose a particular option in a survey. This data point contributes to understanding trends and drawing conclusions.
- Everyday Life: Imagine you have a bag of 50 marbles, and 7 of them are red. The percentage of red marbles is 14%. This simple calculation can be applied to countless everyday scenarios involving proportions.
Addressing Common Questions and Misconceptions
Many students struggle with fraction-to-percentage conversions. Here are some common questions and their answers:
Q: Can I always use the division method?
A: Yes, the division method is a universal approach that works for any fraction. It's a reliable method, especially for fractions that don't easily convert to an equivalent fraction with a denominator of 100.
Q: Why is multiplying by 100% necessary?
A: Multiplying by 100% is crucial because a percentage is defined as a fraction of 100. This step converts the decimal representation of the fraction into its percentage equivalent.
Q: What if the fraction is an improper fraction (numerator > denominator)?
A: The same methods apply. The resulting percentage will be greater than 100%, indicating that the fraction represents more than one whole.
Q: Are there any online tools to help with this conversion?
A: While many online calculators exist to perform this task, understanding the underlying process is crucial for developing mathematical fluency and problem-solving skills.
Expanding on the Concept: Working with Different Fractions
Let's apply these methods to other fractions to further solidify our understanding:
-
15/25 as a percent:
- Division Method: 15 ÷ 25 = 0.6; 0.6 x 100% = 60%
- Equivalent Fraction Method: 15/25 = (15 x 4) / (25 x 4) = 60/100 = 60%
- Proportion Method: 15/25 = x/100; 1500 = 25x; x = 60
-
3/20 as a percent:
- Division Method: 3 ÷ 20 = 0.15; 0.15 x 100% = 15%
- Equivalent Fraction Method: 3/20 = (3 x 5) / (20 x 5) = 15/100 = 15%
- Proportion Method: 3/20 = x/100; 300 = 20x; x = 15
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a critical skill that finds wide application in various contexts. This guide has provided a comprehensive overview of the different methods for converting 7/50 to its percentage equivalent (14%) and has extended this knowledge to other fractions. Understanding these methods ensures proficiency in mathematical calculations and problem-solving. Remember, mastering this concept is not simply about memorizing formulas but about grasping the underlying principles and their practical implications. By practicing these methods with various fractions, you'll build a strong foundation in this essential mathematical skill. The ability to convert fractions to percentages is a cornerstone of numerical literacy, enabling you to confidently interpret and apply mathematical concepts in diverse real-world situations.
Latest Posts
Latest Posts
-
Fundamental Number In Physics Crossword
Sep 18, 2025
-
Examples Of Solving A Problem
Sep 18, 2025
-
Whats 100 Km In Miles
Sep 18, 2025
-
100 Meters In A Kilometer
Sep 18, 2025
-
Conversion Of Kilowatt To Kva
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 7 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.