8 12 As A Percentage
elan
Sep 22, 2025 · 5 min read
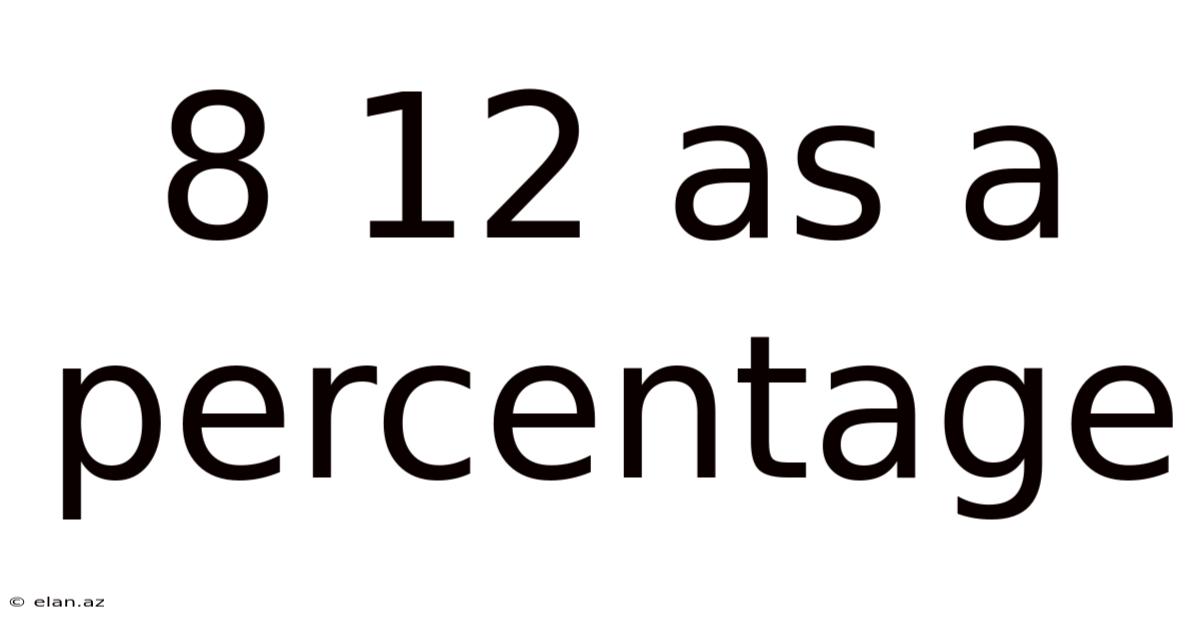
Table of Contents
Understanding 8 of 12 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex scientific analysis. This article delves into the specific calculation of representing 8 out of 12 as a percentage, providing a step-by-step guide suitable for all levels of understanding, along with insightful explanations and practical applications. We will explore the underlying mathematical principles, address common misconceptions, and provide you with the tools to confidently tackle similar percentage problems in the future.
Understanding the Basics of Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." When we say 50%, we mean 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental concept is crucial for mastering percentage calculations.
Calculating 8 out of 12 as a Percentage: A Step-by-Step Approach
To determine what percentage 8 out of 12 represents, we follow these simple steps:
Step 1: Express the values as a fraction.
The problem "8 of 12" can be written as the fraction 8/12. This fraction represents the ratio of the part (8) to the whole (12).
Step 2: Simplify the fraction (optional but recommended).
While not strictly necessary, simplifying the fraction makes the subsequent calculations easier. Both 8 and 12 are divisible by 4, resulting in the simplified fraction 2/3.
Step 3: Convert the fraction to a decimal.
To convert the fraction 2/3 to a decimal, divide the numerator (2) by the denominator (3): 2 ÷ 3 = 0.6666... This decimal representation is a recurring decimal, meaning the digit 6 repeats infinitely.
Step 4: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%). Therefore: 0.6666... × 100 ≈ 66.67%. We round the result to two decimal places for practical purposes.
Therefore, 8 out of 12 is approximately 66.67%.
Different Methods for Calculating Percentages
While the above method is straightforward, let's explore alternative approaches:
Method 1: Direct Percentage Calculation
This method involves directly calculating the percentage without simplifying the fraction:
(8/12) * 100% = (0.6666...) * 100% ≈ 66.67%
Method 2: Using Proportions
We can set up a proportion to solve this problem:
8/12 = x/100
To solve for x (the percentage), we cross-multiply:
12x = 800
x = 800/12 ≈ 66.67%
Understanding the Concept of Recurring Decimals in Percentage Calculations
The result of 8/12 as a percentage involves a recurring decimal (0.666...). This means the digit 6 repeats indefinitely. In practical applications, we round the decimal to a reasonable number of decimal places (e.g., two decimal places, resulting in 66.67%). The level of precision required depends on the context of the problem. For instance, in financial calculations, greater precision might be necessary, while in everyday estimations, rounding to the nearest whole number (67%) might suffice.
Practical Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous situations:
- Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and more.
- Statistics and Data Analysis: Representing data proportions, analyzing survey results, and understanding statistical significance.
- Science and Engineering: Expressing experimental results, calculating efficiency rates, and analyzing data in various fields.
- Everyday Life: Calculating tips, understanding sales, comparing prices, and managing budgets.
Addressing Common Misconceptions
Several common misunderstandings surrounding percentage calculations need clarification:
- Confusing Parts and Wholes: Always clearly identify which value represents the part and which represents the whole before attempting calculations.
- Incorrect Rounding: Round your final answer appropriately to the required level of precision, considering the context. Rounding errors can significantly impact the accuracy of calculations.
- Misinterpreting Percentages: Ensure you understand what the percentage represents relative to the whole. For example, a 10% increase from 100 is 110, not 10.
Frequently Asked Questions (FAQ)
Q1: What if I have a different fraction? How can I apply this method to other percentage calculations?
A1: The method described above is applicable to any fraction. Simply replace 8/12 with your desired fraction, convert it to a decimal, and multiply by 100 to obtain the percentage.
Q2: Why do we sometimes simplify fractions before converting to percentages?
A2: Simplifying fractions can make the calculations easier and reduce the risk of errors, especially when dealing with larger numbers. However, it's not strictly necessary, and either approach will yield the same result.
Q3: What is the difference between a percentage increase and a percentage decrease?
A3: A percentage increase involves adding a percentage of the original value, while a percentage decrease involves subtracting a percentage of the original value.
Q4: How can I calculate the percentage change between two values?
A4: To calculate the percentage change between two values (A and B), use the formula: [(B - A) / A] x 100%. A positive result indicates an increase, while a negative result indicates a decrease.
Conclusion
Understanding how to represent 8 out of 12 as a percentage—approximately 66.67%—is a valuable skill with broad applications. By mastering this fundamental concept and utilizing the methods and strategies outlined above, you can confidently tackle various percentage-related problems. Remember to always clearly identify the part and the whole, simplify fractions where appropriate, and correctly round your final answer. With practice, calculating percentages will become second nature, empowering you to analyze data, make informed decisions, and excel in diverse academic and professional contexts. The key is to break down the problem into manageable steps and understand the underlying mathematical principles. This will not only help you solve specific problems like "8 of 12 as a percentage" but also equip you with a strong foundation for tackling more complex percentage-related calculations in the future.
Latest Posts
Latest Posts
-
Noise Crossword Clue 5 Letters
Sep 22, 2025
-
Mental Arithmetic Answers Book 4
Sep 22, 2025
-
Born Haber Cycle For Mgo
Sep 22, 2025
-
Fruit That Begins With P
Sep 22, 2025
-
Arithmetic Sequence Vs Geometric Sequence
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 8 12 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.