8 X 4 X 2
elan
Sep 16, 2025 · 6 min read
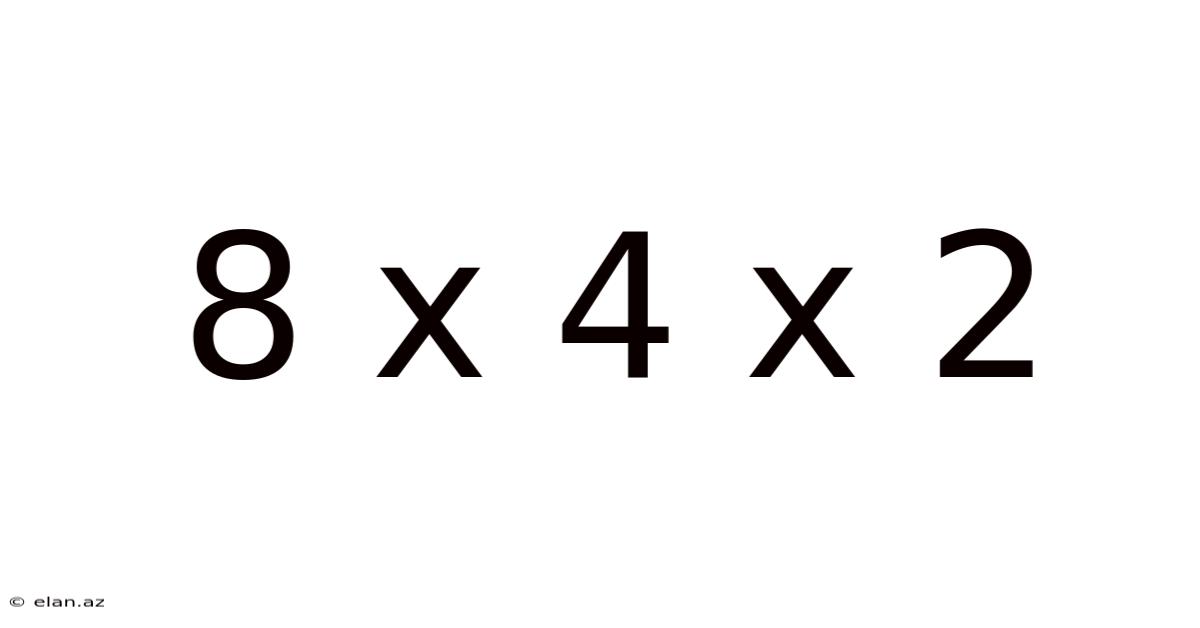
Table of Contents
Decoding 8 x 4 x 2: Exploring Dimensions, Volume, and Applications
This article delves into the seemingly simple expression "8 x 4 x 2," exploring its mathematical implications, practical applications, and the broader concepts it represents. While it might appear basic at first glance, this expression opens doors to understanding fundamental principles in geometry, spatial reasoning, and even problem-solving in various fields. We'll unpack its meaning, explore its uses, and consider its significance beyond a simple multiplication problem.
Introduction: The Fundamentals of 8 x 4 x 2
The expression "8 x 4 x 2" represents a simple multiplication problem, resulting in a product of 64. However, its true significance lies in its potential interpretation as representing the dimensions of a three-dimensional object – specifically, a rectangular prism or cuboid. In this context, 8, 4, and 2 would represent the length, width, and height of the object, respectively, all measured in a consistent unit (e.g., centimeters, inches, meters). Understanding this interpretation unlocks a wealth of related concepts and applications.
Understanding Dimensions and Volume
The three numbers – 8, 4, and 2 – define the dimensions of the rectangular prism. These dimensions are crucial in determining the object's volume. Volume refers to the amount of three-dimensional space occupied by an object. For a rectangular prism, the volume is calculated by multiplying its length, width, and height:
Volume = Length x Width x Height
In our case:
Volume = 8 x 4 x 2 = 64 cubic units
The "cubic units" designation is essential; it indicates that the volume is measured in cubes of the chosen unit. For example, if the dimensions are in centimeters, the volume would be 64 cubic centimeters (cm³).
Visualizing the 8 x 4 x 2 Cuboid
Imagine a box. This box has a length of 8 units, a width of 4 units, and a height of 2 units. You can visualize this by drawing a rectangular prism with these dimensions. This visualization aids in understanding the spatial relationship between the dimensions and the overall volume. Consider building this with blocks – you would need 64 individual blocks to construct the complete prism. This physical representation helps to solidify the abstract concept of volume.
Applications of the 8 x 4 x 2 Concept
The seemingly simple concept of an 8 x 4 x 2 rectangular prism has applications across a surprising range of fields:
-
Packaging and Shipping: Companies use these calculations to determine the size and volume of boxes needed for shipping goods. Optimizing dimensions to minimize wasted space is crucial for efficiency and cost reduction. An 8 x 4 x 2 box might be ideal for a specific product, maximizing space utilization while adhering to shipping regulations.
-
Construction and Engineering: Architects and engineers frequently work with volumes and dimensions. Understanding volume is essential for calculating material requirements (like concrete for foundations or bricks for walls), estimating costs, and ensuring structural integrity. An understanding of volume, derived from dimensions like 8 x 4 x 2, is fundamental.
-
Manufacturing and Production: Manufacturers use dimensional analysis extensively. From designing molds for casting to calculating the capacity of storage tanks, precise knowledge of volume and dimensions is critical. An 8 x 4 x 2 mold, for example, could be used for producing specific parts or components.
-
Data Storage and Computing: While seemingly unrelated, the concept of volume also extends to data storage. Imagine a data storage unit (perhaps conceptualized as a cube) with a certain capacity. Understanding the “volume” of data that can be stored within the unit is paramount for efficient data management and resource allocation.
-
Everyday Life: Even in daily life, understanding dimensions and volume is frequently important. Consider choosing furniture (a cupboard, a shelf unit) or planning the layout of a room. Accurate estimations of volume help ensure optimal space utilization and functionality.
Extending the Concept: Beyond Rectangular Prisms
While we've focused on rectangular prisms, the principle of multiplying dimensions to find volume extends to other shapes. While the calculation differs, the underlying principle remains consistent. The formula changes based on the shape in question. Understanding this core principle is crucial for broader applications in geometry and related fields.
Exploring Variations and Scalability
The 8 x 4 x 2 example can be easily scaled. Imagine doubling each dimension: 16 x 8 x 4. The volume increases dramatically (512 cubic units), illustrating the non-linear relationship between dimensions and volume. Conversely, halving each dimension would significantly reduce the volume. This scalability demonstrates the sensitivity of volume to changes in dimensions.
Mathematical Connections and Further Exploration
The concept of 8 x 4 x 2 connects to several mathematical concepts:
-
Factors and Multiples: The numbers 8, 4, and 2 have relationships as factors and multiples. Understanding these relationships enriches mathematical understanding.
-
Prime Factorization: Breaking down the numbers into prime factors (2 x 2 x 2, 2 x 2, and 2) provides a deeper mathematical insight. This process reveals the fundamental building blocks of the dimensions.
-
Surface Area: While we focused on volume, calculating the surface area of an 8 x 4 x 2 prism is another important geometrical concept. This involves calculating the area of each face and summing them together.
Frequently Asked Questions (FAQs)
Q: What if the units of measurement are different?
A: You cannot directly multiply dimensions with different units. All dimensions must be expressed in the same unit (e.g., all in centimeters, all in inches) before calculating the volume.
Q: Can this be applied to irregular shapes?
A: No, the 8 x 4 x 2 calculation is specific to rectangular prisms. Calculating the volume of irregular shapes requires more complex methods, often involving integration in calculus.
Q: What are some real-world examples beyond those mentioned?
A: Consider the volume of a fish tank, the capacity of a storage container, the space occupied by a piece of furniture, or the amount of soil needed for a garden bed. The concept is surprisingly widespread.
Q: How can I improve my understanding of volume and dimensions?
A: Practice calculating the volumes of various rectangular prisms with different dimensions. Try building physical models using blocks or other materials to visualize the relationships between dimensions and volume.
Conclusion: The Significance of Understanding 8 x 4 x 2
The seemingly simple expression "8 x 4 x 2" serves as a gateway to understanding fundamental concepts in geometry, spatial reasoning, and practical applications across numerous fields. It's not merely a multiplication problem; it's a representation of dimensions, volume, and the power of mathematical principles in solving real-world problems. By understanding the implications of this seemingly simple calculation, we gain a richer appreciation for the mathematical foundations that underpin our world. From designing buildings to packaging products, the ability to visualize and calculate volume is a vital skill with broad applicability. The seemingly simple calculation of 8 x 4 x 2 is a testament to the power of basic mathematics and its relevance in a complex world.
Latest Posts
Latest Posts
-
Letters Of The Alphabet Images
Sep 16, 2025
-
Arrangement Of Particles In Solid
Sep 16, 2025
-
Rotational Symmetry Of Order 4
Sep 16, 2025
-
Is Brazil Larger Than Australia
Sep 16, 2025
-
Milton Keynes Theory Test Centre
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 8 X 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.