80 Percent As A Fraction
elan
Sep 20, 2025 · 5 min read
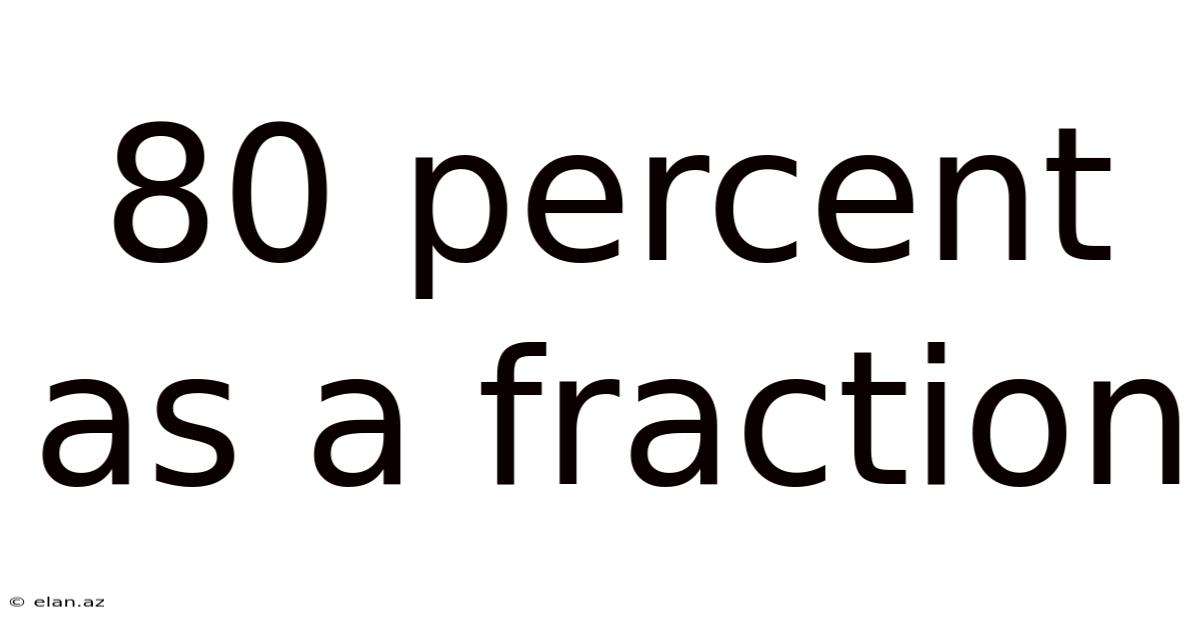
Table of Contents
80 Percent as a Fraction: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics, applicable in countless everyday situations, from calculating discounts in shopping to comprehending statistical data. This article delves deep into expressing 80 percent as a fraction, exploring various methods, simplifying the fraction to its lowest terms, and providing context through real-world examples and frequently asked questions. We'll also touch upon the broader concept of converting percentages to fractions and vice-versa. By the end, you'll not only know how to represent 80% as a fraction but also have a solid grasp of the underlying principles involved.
Understanding Percentages and Fractions
Before jumping into the specifics of 80%, let's review the fundamental relationship between percentages and fractions. A percentage represents a fraction of 100. The word "percent" literally means "out of 100" ( per cent). Therefore, any percentage can be easily converted into a fraction by placing the percentage value over 100.
For example, 50% is equivalent to 50/100, 25% is 25/100, and so on. This fundamental understanding is the key to converting any percentage into its fractional equivalent.
Converting 80% to a Fraction: The Step-by-Step Guide
Converting 80% to a fraction is a straightforward process, following these simple steps:
-
Write the percentage as a fraction: The first step involves writing the percentage number as the numerator (the top part) of a fraction, and 100 as the denominator (the bottom part). Therefore, 80% becomes 80/100.
-
Simplify the fraction: The fraction 80/100 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of both the numerator and denominator. The GCD is the largest number that divides both 80 and 100 without leaving a remainder. In this case, the GCD is 20.
-
Divide both numerator and denominator by the GCD: Divide both the numerator (80) and the denominator (100) by the GCD (20):
80 ÷ 20 = 4 100 ÷ 20 = 5
-
Express the simplified fraction: This gives us the simplified fraction 4/5. Therefore, 80% expressed as a fraction in its simplest form is 4/5.
Visualizing 80% as a Fraction
Imagine a pizza cut into 5 equal slices. If you eat 4 out of those 5 slices, you've eaten 4/5 of the pizza. This visually represents 80% (4 out of 5 slices representing 80 out of 100). This visualization helps solidify the understanding that 4/5 and 80% are equivalent representations of the same proportion.
Different Methods for Converting Percentages to Fractions
While the method described above is the most straightforward, there are other approaches to converting percentages to fractions:
-
Using decimals as an intermediary step: You can first convert the percentage to a decimal by dividing it by 100. 80% divided by 100 is 0.8. Then, you can convert the decimal to a fraction. 0.8 can be written as 8/10, which simplifies to 4/5.
-
Direct simplification: For some percentages, you might be able to simplify the fraction directly without explicitly calculating the GCD. For example, you might recognize that both 80 and 100 are divisible by 10, giving you 8/10, which can then be further simplified to 4/5. This method relies on recognizing common factors and might not be as efficient for all percentages.
Real-World Applications of 80% as a Fraction (4/5)
The representation of 80% as 4/5 has various practical applications:
-
Discounts: A store offering an 80% discount means you pay only 20% of the original price. This can be expressed as 2/5 of the original price (1-4/5 = 1/5).
-
Surveys and statistics: If 80% of respondents in a survey favored a particular candidate, this implies that 4 out of every 5 respondents supported the candidate.
-
Financial calculations: Calculating interest, profits, or losses often involves dealing with percentages, which can be easily converted to fractions for easier calculations, especially when dealing with complex scenarios.
-
Recipe scaling: If a recipe calls for a certain amount of an ingredient and you want to make only 80% of the recipe, you can use the fraction 4/5 to calculate the adjusted quantity of each ingredient.
Frequently Asked Questions (FAQ)
Q1: Can I express 80% as any other fraction besides 4/5?
A1: While 4/5 is the simplest form, you can express 80% as other equivalent fractions, such as 8/10, 16/20, 40/50, and so on. However, these are not as concise and efficient as 4/5.
Q2: How do I convert a fraction back into a percentage?
A2: To convert a fraction back to a percentage, divide the numerator by the denominator and multiply the result by 100. For example, to convert 4/5 back to a percentage: (4 ÷ 5) × 100 = 80%.
Q3: What if I have a percentage with a decimal, like 80.5%?
A3: For percentages with decimals, you follow the same process. 80.5% becomes 80.5/100. You can then simplify by multiplying both numerator and denominator by 10 to remove the decimal (805/1000), and then find the GCD to simplify further. In this case, the simplified fraction is 161/200.
Q4: Are there any situations where using the fraction 4/5 is more advantageous than using 80%?
A4: Yes, using the fraction 4/5 can be more advantageous in scenarios where dealing with fractions is easier or more intuitive than using percentages. For example, when performing multiplication or division of proportions, working with fractions often leads to simpler calculations. Also, in some contexts, expressing a portion as a fraction provides a more precise representation, especially when the denominator is a small number.
Conclusion
Converting 80% to a fraction, and more broadly understanding the relationship between percentages and fractions, is a crucial skill in various mathematical contexts and everyday life. The simplest form of 80% as a fraction is 4/5, obtained by writing 80/100 and simplifying it by dividing both numerator and denominator by their greatest common divisor, 20. Understanding the different methods of conversion and their real-world applications enhances the ability to confidently tackle problems involving proportions and percentages. The ability to seamlessly translate between percentages and fractions enables more flexible and efficient problem-solving in numerous quantitative applications. Mastering this fundamental concept opens doors to a deeper understanding of more advanced mathematical concepts.
Latest Posts
Latest Posts
-
2000 Square Feet To Meters
Sep 20, 2025
-
5 Letter Words Ending Ae
Sep 20, 2025
-
Ethane Dot And Cross Diagram
Sep 20, 2025
-
Can You Retract A Resignation
Sep 20, 2025
-
Angles Around A Point Worksheet
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 80 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.