9 10 As A Percent
elan
Sep 13, 2025 · 5 min read
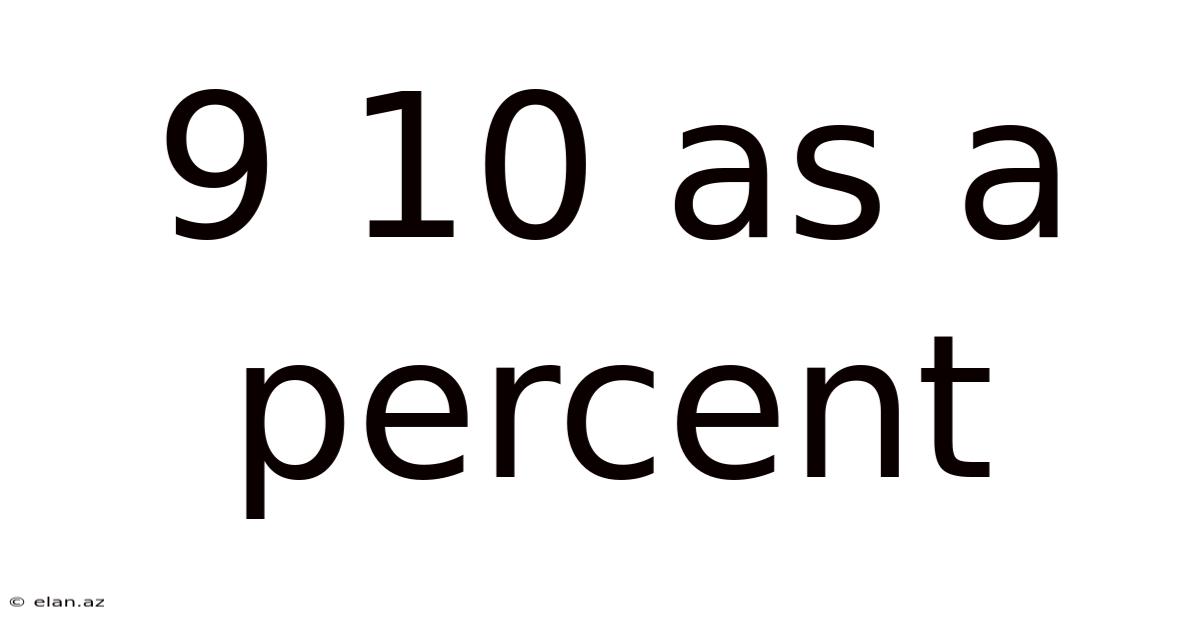
Table of Contents
Decoding 9/10 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to analyzing data and understanding statistics. This article provides a comprehensive guide to understanding how to convert the fraction 9/10 into a percentage, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll delve into different methods, ensuring you not only get the answer but also grasp the underlying concepts.
Understanding Fractions and Percentages
Before diving into the conversion of 9/10 to a percentage, let's establish a clear understanding of both fractions and percentages.
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 9/10, 9 represents the number of parts we have, and 10 represents the total number of equal parts.
A percentage, denoted by the symbol %, represents a fraction where the denominator is always 100. It indicates a proportion out of 100. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or simplified, 1/2.
The key to converting a fraction to a percentage lies in understanding that we are essentially expressing the fraction as an equivalent fraction with a denominator of 100.
Method 1: Direct Conversion Using Division
The most straightforward method to convert 9/10 to a percentage involves a simple division:
-
Divide the numerator by the denominator: Divide 9 by 10. This gives you 0.9.
-
Multiply by 100: To convert the decimal to a percentage, multiply the result (0.9) by 100. This gives you 90.
-
Add the percentage symbol: Finally, add the percentage symbol (%) to indicate that the result is a percentage.
Therefore, 9/10 is equal to 90%.
Method 2: Equivalent Fractions
This method focuses on creating an equivalent fraction with a denominator of 100. Since percentages are fractions with a denominator of 100, this method offers a clear visual representation of the conversion.
-
Find the multiplier: Determine what number you need to multiply the denominator (10) by to get 100. In this case, 10 multiplied by 10 equals 100.
-
Multiply both the numerator and denominator: To maintain the value of the fraction, you must multiply both the numerator and the denominator by the same number. So, multiply 9 (numerator) and 10 (denominator) by 10. This gives you 90/100.
-
Express as a percentage: Since 90/100 means 90 out of 100, this directly translates to 90%.
Method 3: Using Proportions
This method utilizes the concept of proportions, demonstrating the relationship between the fraction and its percentage equivalent.
We can set up a proportion:
9/10 = x/100
Where 'x' represents the percentage we're trying to find.
To solve for 'x', we cross-multiply:
10x = 900
Then, divide both sides by 10:
x = 90
Therefore, 9/10 is equal to 90%.
Mathematical Explanation: Why does this work?
The methods above all stem from the fundamental definition of a percentage. A percentage is a fraction out of 100. Converting a fraction to a percentage simply involves finding an equivalent fraction with a denominator of 100. The division method achieves this by essentially dividing the numerator by the denominator to find the decimal equivalent, which represents the proportion of the whole. Multiplying by 100 then scales this proportion to represent it as a value out of 100. The equivalent fraction method explicitly shows this scaling by multiplying both the numerator and denominator by the same factor to create the equivalent fraction with a denominator of 100. The proportions method directly establishes the relationship between the fraction and the percentage, allowing for a solution through algebraic manipulation.
Real-world Applications of 9/10 and 90%
Understanding the equivalence of 9/10 and 90% has numerous practical applications:
- Grading: A score of 9/10 on a test translates to a 90% grade.
- Sales and discounts: A 90% discount means you pay only 10% of the original price.
- Statistics and data analysis: Representing data proportions using percentages is common, making this conversion crucial for interpretation.
- Probability: The likelihood of an event occurring can be represented as a fraction or a percentage.
Frequently Asked Questions (FAQ)
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage using the methods described above. However, some fractions may result in percentages with decimal places.
Q: What if the denominator isn't a factor of 100?
A: You can still use the division method. Divide the numerator by the denominator, and then multiply the result by 100 to get the percentage.
Q: Is there a quicker way to convert fractions with a denominator of 10, 100, or 1000?
A: Yes. For denominators of 10, simply move the decimal point one place to the right and add the percentage sign. For 100, move the decimal point two places to the right, and for 1000, move it three places.
Q: What if I get a repeating decimal when I divide the numerator by the denominator?
A: This means the percentage will also have a repeating decimal. You can round the percentage to a certain number of decimal places for practical purposes.
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare proportions and understand data across different contexts. They simplify the interpretation of ratios and fractions, making them easily understandable and applicable in various fields.
Conclusion
Converting 9/10 to a percentage is a simple yet fundamental mathematical operation. Understanding the different methods—direct division, equivalent fractions, and proportions—helps solidify the concept and allows you to confidently handle similar conversions in diverse situations. The ability to convert fractions to percentages is not just a mathematical skill; it's a practical tool essential for navigating numerous aspects of everyday life and professional endeavors. Mastering this conversion equips you with the ability to interpret data, make informed decisions, and confidently tackle percentage-related problems. Remember to practice regularly to reinforce your understanding and build fluency in these vital mathematical skills.
Latest Posts
Latest Posts
-
Why Is Air A Mixture
Sep 13, 2025
-
A Level Maths Factor Theorem
Sep 13, 2025
-
Plants That Begin With J
Sep 13, 2025
-
Common And Proper Nouns Worksheets
Sep 13, 2025
-
Advantages Of Non Renewable Energy
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 9 10 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.