9 5 As A Percent
elan
Sep 15, 2025 · 5 min read
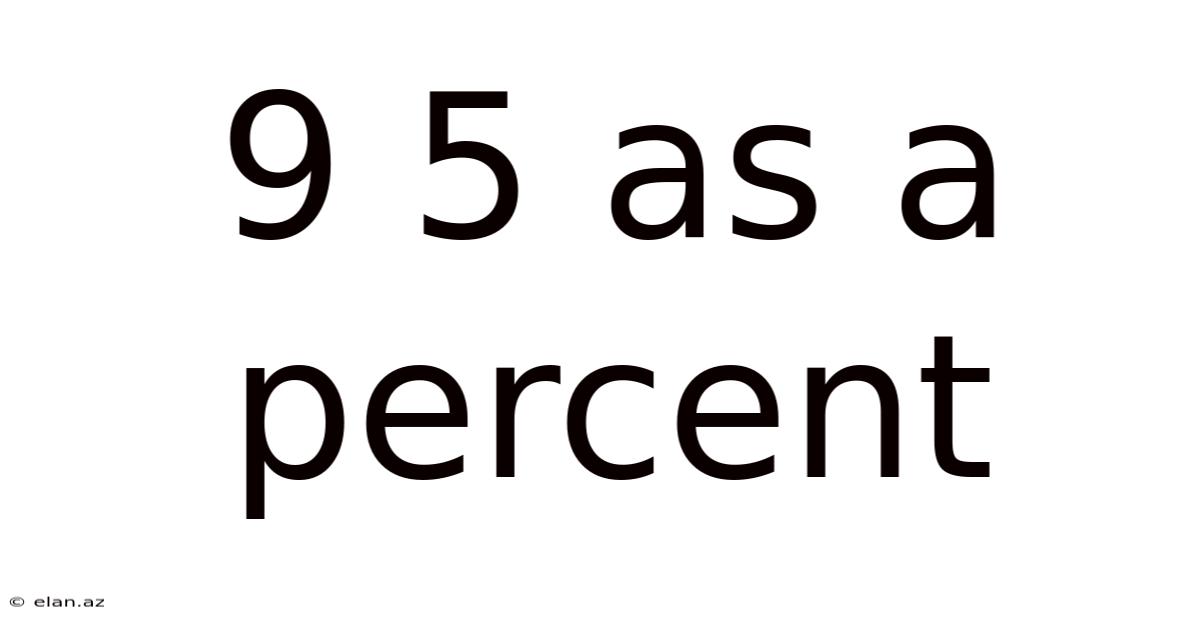
Table of Contents
9/5 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday calculations. This comprehensive guide will delve into the process of converting the fraction 9/5 into a percentage, explaining the steps involved and providing additional context for a thorough understanding. We'll explore various methods, address common misconceptions, and offer practical examples to solidify your comprehension. This guide is designed for learners of all levels, from beginners seeking a basic understanding to those aiming to master fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the conversion of 9/5, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
A percentage, denoted by the symbol %, represents a fraction of 100. It signifies a proportion out of a hundred. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Converting 9/5 to a Percentage: Step-by-Step Guide
There are several ways to convert the improper fraction 9/5 into a percentage. Let's explore the most common methods:
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most straightforward method. First, we convert the fraction into a decimal by dividing the numerator by the denominator:
9 ÷ 5 = 1.8
Now, to convert the decimal to a percentage, we multiply by 100:
1.8 x 100 = 180
Therefore, 9/5 is equal to 180%.
Method 2: Direct Conversion using Proportions
We can also solve this using a proportion. We know that a percentage is a fraction out of 100. So, we can set up the following proportion:
9/5 = x/100
To solve for 'x' (the percentage), we cross-multiply:
9 * 100 = 5 * x
900 = 5x
x = 900 ÷ 5
x = 180
Again, we find that 9/5 is equal to 180%.
Method 3: Understanding the Concept of Improper Fractions
The fraction 9/5 is an improper fraction because the numerator (9) is larger than the denominator (5). This means the fraction represents a value greater than 1. When converting improper fractions to percentages, we will always get a percentage greater than 100%. This is perfectly valid and simply indicates that the fraction represents more than one whole. Think of it as having one whole (5/5) and an additional 4/5.
Visual Representation: Understanding 180%
It's helpful to visualize what 180% represents. Imagine a bar representing 100%. 180% would be a bar that is 100% long, plus an additional 80% extension. It’s 80% longer than the original 100%. This visual understanding helps to contextualize the meaning of a percentage greater than 100%.
Practical Applications of 9/5 and 180%
The conversion of 9/5 to 180% finds application in various real-world scenarios. For instance:
-
Percentage Increase: If a quantity increases by 9/5, it means it has increased by 180%. This could represent a price increase, a population growth, or an increase in production.
-
Financial Calculations: In finance, understanding percentage increases and decreases is crucial for calculating profits, losses, interest rates, and more. Converting fractions like 9/5 to percentages makes such calculations straightforward.
-
Data Analysis: When dealing with data analysis and statistics, representing changes as percentages often offers a clearer picture than using fractions. Converting to percentages simplifies comparisons and interpretations.
Addressing Common Misconceptions
A common misconception is that percentages must always be between 0% and 100%. This is incorrect. Percentages can be greater than 100%, as demonstrated by our example of 9/5 = 180%. They can also be negative, representing a decrease in value.
Another misconception is the confusion between fractions and decimals. While decimals are a way to represent parts of a whole, just like fractions, percentages are a specific representation of those parts as a fraction of 100. Therefore, we need an extra step to convert decimals to percentages (multiplying by 100).
Frequently Asked Questions (FAQ)
-
Q: Can all fractions be converted to percentages?
-
A: Yes, all fractions can be converted to percentages by dividing the numerator by the denominator and then multiplying by 100.
-
Q: What if the fraction is a mixed number (e.g., 1 4/5)?
-
A: Convert the mixed number to an improper fraction first. For example, 1 4/5 becomes (5 + 4)/5 = 9/5. Then, follow the steps outlined above.
-
Q: How do I convert a percentage back to a fraction?
-
A: Divide the percentage by 100 and simplify the resulting fraction. For example, 180% becomes 180/100, which simplifies to 9/5.
-
Q: Why is understanding percentage conversions important?
-
A: Percentage conversions are crucial for comparing quantities, understanding growth and decline, and performing various calculations in many fields. They are essential for interpreting data and making informed decisions.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with broad applications. The conversion of 9/5 to 180% exemplifies the process of dealing with improper fractions and understanding percentages exceeding 100%. Through various methods – direct conversion, decimal conversion, and proportional methods – we have explored multiple approaches to arrive at the correct answer. Mastering these techniques empowers you to confidently tackle various mathematical problems and interpret data effectively in a variety of contexts. Remember to visualize the meaning of the percentage to gain a deeper understanding, ensuring that the numerical answer is also conceptually sound. This comprehensive guide provides a solid foundation for further exploration into percentage calculations and their diverse applications.
Latest Posts
Latest Posts
-
What Is Cationic And Anionic
Sep 15, 2025
-
12 25 As A Percentage
Sep 15, 2025
-
Words To Describe The Beach
Sep 15, 2025
-
1 Million Pounds To Rupees
Sep 15, 2025
-
Equation For Gravitational Field Strength
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 9 5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.