Factor 3x 2 5x 2
elan
Sep 16, 2025 · 6 min read
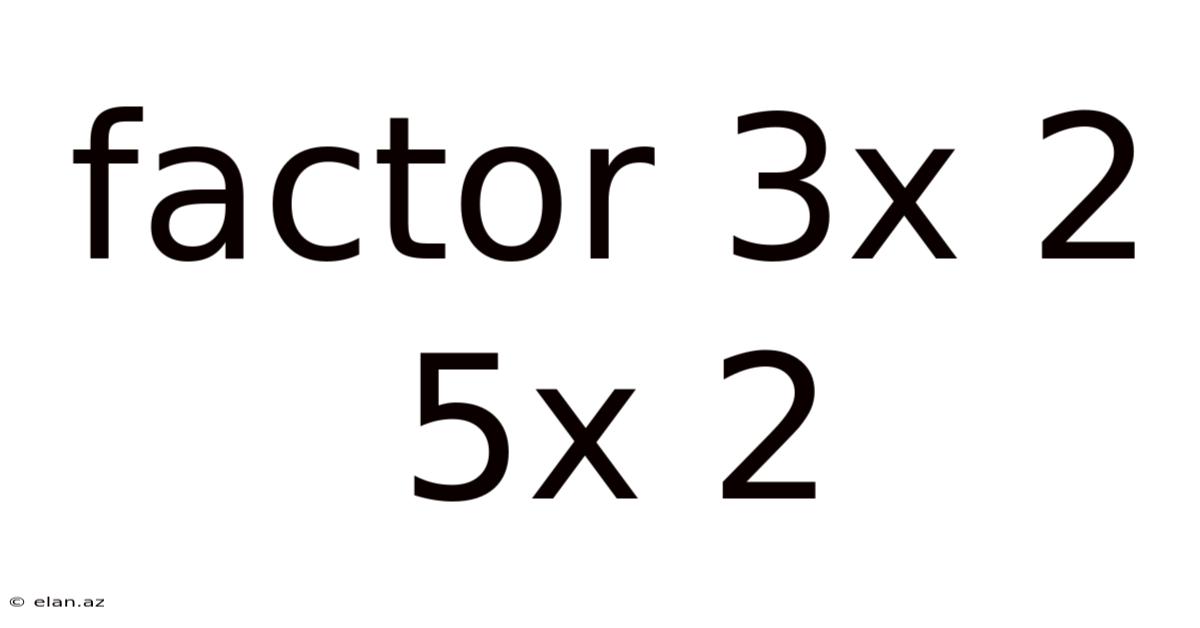
Table of Contents
Factoring Trinomials: A Deep Dive into 3x² + 5x + 2
Factoring quadratic expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding various mathematical concepts. This article will provide a comprehensive guide to factoring the trinomial 3x² + 5x + 2, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing common questions. We'll cover various methods, enabling you to tackle similar problems with confidence. Understanding this process unlocks the door to more advanced algebraic manipulations.
Understanding the Problem: 3x² + 5x + 2
Our task is to factor the quadratic trinomial 3x² + 5x + 2. This means we need to express it as a product of two simpler expressions, typically binomials. The goal is to find two binomials that, when multiplied together, result in the original trinomial. This process is the reverse of expanding binomials using the distributive property (often called FOIL).
Method 1: The AC Method (Factoring by Grouping)
This method is a systematic approach that works for most quadratic trinomials, especially those with a leading coefficient (the coefficient of x²) greater than 1. Here’s how it works for 3x² + 5x + 2:
-
Identify a, b, and c: In the trinomial ax² + bx + c, we have a = 3, b = 5, and c = 2.
-
Find the product ac: The product ac is 3 * 2 = 6.
-
Find two numbers that add up to b and multiply to ac: We need two numbers that add up to 5 (our b value) and multiply to 6 (our ac value). These numbers are 3 and 2 (3 + 2 = 5 and 3 * 2 = 6).
-
Rewrite the middle term: Rewrite the middle term (5x) as the sum of the two numbers we found, multiplied by x: 3x + 2x. Our trinomial now becomes 3x² + 3x + 2x + 2.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
3x² + 3x + 2x + 2 = 3x(x + 1) + 2(x + 1)
-
Factor out the common binomial: Notice that both terms now share the common binomial (x + 1). Factor this out:
3x(x + 1) + 2(x + 1) = (3x + 2)(x + 1)
Therefore, the factored form of 3x² + 5x + 2 is (3x + 2)(x + 1).
Method 2: Trial and Error
This method involves a bit of educated guessing but can be faster once you get the hang of it. It relies on understanding how binomial multiplication works.
-
Set up the binomial factors: We know the factored form will be something like (ax + b)(cx + d), where a, b, c, and d are numbers.
-
Consider the first term: The product of the first terms in each binomial must equal 3x². Since 3 is a prime number, the only possibilities are (3x )(x ).
-
Consider the last term: The product of the last terms in each binomial must equal 2. The possible pairs of factors are (1, 2) and (-1, -2).
-
Test the combinations: Let's try different combinations:
- (3x + 1)(x + 2): Expanding this gives 3x² + 7x + 2 (incorrect)
- (3x + 2)(x + 1): Expanding this gives 3x² + 5x + 2 (correct!)
Therefore, the factored form is again (3x + 2)(x + 1).
Mathematical Explanation: Why Factoring Works
The AC method and trial and error are both based on the distributive property of multiplication. When we expand (3x + 2)(x + 1), we use the FOIL method (First, Outer, Inner, Last):
- First: (3x)(x) = 3x²
- Outer: (3x)(1) = 3x
- Inner: (2)(x) = 2x
- Last: (2)(1) = 2
Combining these terms, we get 3x² + 3x + 2x + 2 = 3x² + 5x + 2. Factoring reverses this process, finding the original binomials from the expanded trinomial.
Addressing Common Mistakes
- Incorrect signs: Be mindful of positive and negative signs when choosing factors. Make sure the combination of factors results in the correct middle term.
- Missing factors: Ensure you've considered all possible factor pairs for both the leading coefficient and the constant term.
- Not checking your answer: Always expand your factored form to verify that it matches the original trinomial.
Beyond 3x² + 5x + 2: Factoring Other Trinomials
The techniques described here – the AC method and trial and error – are applicable to a wide range of quadratic trinomials. The key is to understand the principles of the distributive property and systematically explore possible factor combinations. For trinomials with larger coefficients, the AC method provides a more structured and less error-prone approach.
Further Exploration: More Complex Quadratics
While we focused on 3x² + 5x + 2, the concepts extend to more complicated quadratic expressions. These might include:
- Trinomials with a negative leading coefficient: These require careful consideration of negative factors.
- Trinomials with a greatest common factor (GCF): Always factor out the GCF before attempting to factor the remaining trinomial.
- Trinomials that are not factorable: Some quadratic trinomials cannot be factored using integers. These are often solved using the quadratic formula.
Frequently Asked Questions (FAQ)
Q: What if the trinomial has a greatest common factor (GCF)?
A: Always look for a GCF first. For example, if you had 6x² + 10x + 4, you would first factor out the GCF of 2, leaving 2(3x² + 5x + 2). Then, you would factor the trinomial inside the parentheses using the methods described above.
Q: Can I use the quadratic formula to solve this?
A: While the quadratic formula can find the roots (solutions) of the equation 3x² + 5x + 2 = 0, it doesn't directly give the factored form. Factoring is a separate but related process.
Q: What if I can't find the factors easily?
A: If you're struggling with trial and error, the AC method provides a more systematic approach. Practice is key – the more you practice factoring, the faster and more intuitive the process will become.
Q: Are there other factoring methods?
A: Yes, there are other methods, but the AC method and trial and error are the most commonly used for trinomials of this type. Other methods might be more suitable for certain special cases, such as perfect square trinomials or difference of squares.
Conclusion
Factoring the trinomial 3x² + 5x + 2, resulting in (3x + 2)(x + 1), is a valuable exercise in understanding the fundamental principles of algebra. By mastering the AC method and trial and error, you develop essential skills for solving equations, simplifying expressions, and tackling more complex mathematical problems. Remember to practice regularly, and don't hesitate to review the steps and explanations provided in this article. With consistent effort, you'll build confidence and proficiency in factoring quadratic expressions. The journey to mastering algebra is a rewarding one, filled with the satisfaction of unlocking mathematical puzzles and gaining a deeper appreciation for the beauty and logic inherent within.
Latest Posts
Latest Posts
-
2 Million Rupees In Pounds
Sep 16, 2025
-
Poem About Losing A Dog
Sep 16, 2025
-
Moment Of Area I Beam
Sep 16, 2025
-
Advantages Of Break Even Analysis
Sep 16, 2025
-
How Big Is 5 Inches
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor 3x 2 5x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.