Graph Of Y 2x 1
elan
Sep 14, 2025 · 7 min read
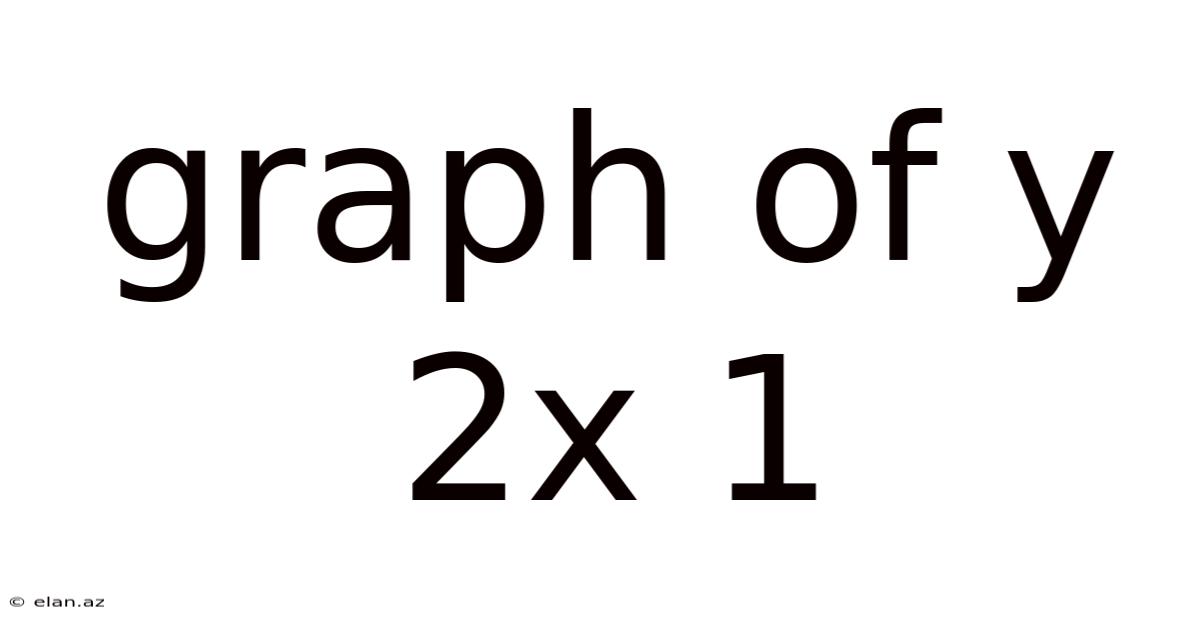
Table of Contents
Exploring the Graph of y = 2x + 1: A Comprehensive Guide
Understanding the graph of a linear equation like y = 2x + 1 is fundamental to mastering algebra and its applications. This equation represents a straight line, and its graphical representation reveals key characteristics about its slope, y-intercept, and overall behavior. This comprehensive guide will delve into the intricacies of this seemingly simple equation, exploring its properties, how to graph it, and its broader mathematical significance.
I. Introduction: Unveiling the Linear Equation
The equation y = 2x + 1 is a linear equation in two variables, x and y. This means its graph will always be a straight line. The equation is in the slope-intercept form, y = mx + b, where 'm' represents the slope of the line and 'b' represents the y-intercept (the point where the line crosses the y-axis). In our equation, m = 2 and b = 1. This immediately tells us crucial information about the line's appearance and behavior before we even begin plotting points.
II. Understanding the Slope (m = 2)
The slope, 2, indicates the steepness and direction of the line. A positive slope means the line rises from left to right. Specifically, a slope of 2 means that for every 1-unit increase in the x-value, the y-value increases by 2 units. This can be visualized as a "rise over run" ratio of 2/1. Conversely, for every 1-unit decrease in x, the y-value decreases by 2 units. This consistent ratio is what defines the straightness of the line. A larger slope indicates a steeper line; a smaller positive slope indicates a gentler incline.
III. Understanding the Y-intercept (b = 1)
The y-intercept, 1, tells us where the line crosses the y-axis. The y-axis is the vertical line where x = 0. When x = 0 in our equation, y = 2(0) + 1 = 1. This means the line passes through the point (0, 1). This point is a crucial starting point when graphing the line.
IV. Graphing the Equation: A Step-by-Step Approach
There are several ways to graph the equation y = 2x + 1:
-
Method 1: Using the Slope and Y-intercept:
- Plot the y-intercept: Begin by plotting the point (0, 1) on the coordinate plane.
- Use the slope to find another point: The slope is 2/1. From the y-intercept (0, 1), move 1 unit to the right (run) and 2 units up (rise). This brings you to the point (1, 3).
- Draw the line: Draw a straight line passing through the points (0, 1) and (1, 3). Extend the line in both directions to represent the infinite nature of the linear equation.
-
Method 2: Using a Table of Values:
- Choose x-values: Select a few x-values, such as -2, -1, 0, 1, and 2.
- Calculate corresponding y-values: Substitute each x-value into the equation y = 2x + 1 to find the corresponding y-value.
- When x = -2, y = 2(-2) + 1 = -3
- When x = -1, y = 2(-1) + 1 = -1
- When x = 0, y = 2(0) + 1 = 1
- When x = 1, y = 2(1) + 1 = 3
- When x = 2, y = 2(2) + 1 = 5
- Plot the points: Plot the points (-2, -3), (-1, -1), (0, 1), (1, 3), and (2, 5) on the coordinate plane.
- Draw the line: Draw a straight line passing through these points.
-
Method 3: Using Technology:
Graphing calculators and online graphing tools can easily plot the equation y = 2x + 1. Simply input the equation and the tool will generate the graph, often allowing for interactive exploration and zooming.
V. Interpreting the Graph
The graph of y = 2x + 1 is a straight line that slopes upward from left to right. It intersects the y-axis at the point (0, 1) and has a slope of 2. Every point on the line satisfies the equation y = 2x + 1. The graph visually represents all possible solutions to the equation. For example, you can see that the point (2, 5) lies on the line because when x = 2, y = 2(2) + 1 = 5.
VI. Extending the Concepts: Parallel and Perpendicular Lines
Understanding the slope allows us to explore relationships between lines.
-
Parallel Lines: Any line parallel to y = 2x + 1 will have the same slope, 2, but a different y-intercept. For example, y = 2x + 5 is parallel to y = 2x + 1. Parallel lines never intersect.
-
Perpendicular Lines: A line perpendicular to y = 2x + 1 will have a slope that is the negative reciprocal of 2, which is -1/2. For example, y = -1/2x + 3 is perpendicular to y = 2x + 1. Perpendicular lines intersect at a 90-degree angle.
VII. Real-World Applications
Linear equations like y = 2x + 1 have numerous real-world applications. They can model:
-
Cost Functions: Imagine a taxi fare where the initial charge is $1 (y-intercept) and the cost per mile is $2 (slope). The total cost (y) would be a function of the number of miles (x).
-
Speed and Distance: If an object travels at a constant speed of 2 units per second, starting at a position of 1 unit, its position (y) at any time (x) can be represented by this equation.
-
Temperature Conversions: While not a perfect fit, linear equations can approximate conversions between temperature scales (Celsius and Fahrenheit, for example) over a specific range.
VIII. Solving Equations and Inequalities Graphically
The graph can also be used to solve equations and inequalities involving the line.
-
Solving for y: For any given x-value, the corresponding y-value can be read directly from the graph.
-
Solving for x: Similarly, for any given y-value, the corresponding x-value can be determined from the graph.
-
Solving Inequalities: The graph can be used to visualize solutions to inequalities such as y > 2x + 1 (the region above the line) or y < 2x + 1 (the region below the line).
IX. Advanced Concepts: Systems of Equations
Multiple linear equations can be graphed on the same coordinate plane. The point(s) where the lines intersect represent the solution(s) to the system of equations. For example, if we had a second equation, say y = x + 2, the intersection point of this line and y = 2x + 1 would represent the (x,y) pair that satisfies both equations simultaneously.
X. Further Exploration: Non-Linear Functions
While y = 2x + 1 is a linear equation, understanding its graph forms a strong foundation for exploring non-linear functions. Concepts like slope and intercepts can be extended (in modified forms) to understand the behavior of curves and other more complex mathematical relationships.
XI. Frequently Asked Questions (FAQ)
-
Q: What if the slope is negative? A: A negative slope indicates that the line falls from left to right. The steeper the negative slope, the faster the line falls.
-
Q: What if the y-intercept is 0? A: If the y-intercept is 0, the line passes through the origin (0, 0). The equation would simplify to y = mx.
-
Q: Can I use any two points to graph a line? A: Yes, any two distinct points that satisfy the equation can be used to graph the line.
-
Q: What happens if the equation is not in slope-intercept form? A: Equations can be rearranged to be in slope-intercept form (y = mx + b) to easily identify the slope and y-intercept.
-
Q: How can I check if a point is on the line? A: Substitute the x and y coordinates of the point into the equation. If the equation holds true, the point lies on the line.
XII. Conclusion: A Foundation for Further Learning
The seemingly simple graph of y = 2x + 1 provides a rich foundation for understanding linear equations, their graphical representations, and their various applications. Mastering this concept opens doors to more advanced mathematical topics, from solving systems of equations to calculus and beyond. The ability to visualize and interpret linear graphs is a critical skill for success in mathematics and related fields. Through careful study and practice, you can confidently navigate the world of linear equations and unlock their power to solve real-world problems.
Latest Posts
Latest Posts
-
Exact Values For Trig Functions
Sep 14, 2025
-
300 Square Feet To Metres
Sep 14, 2025
-
Is Displacement A Vector Quantity
Sep 14, 2025
-
Words That Start With Mon
Sep 14, 2025
-
Hcf And Lcm Venn Diagram
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Graph Of Y 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.