Hcf Of 210 And 308
elan
Sep 14, 2025 · 6 min read
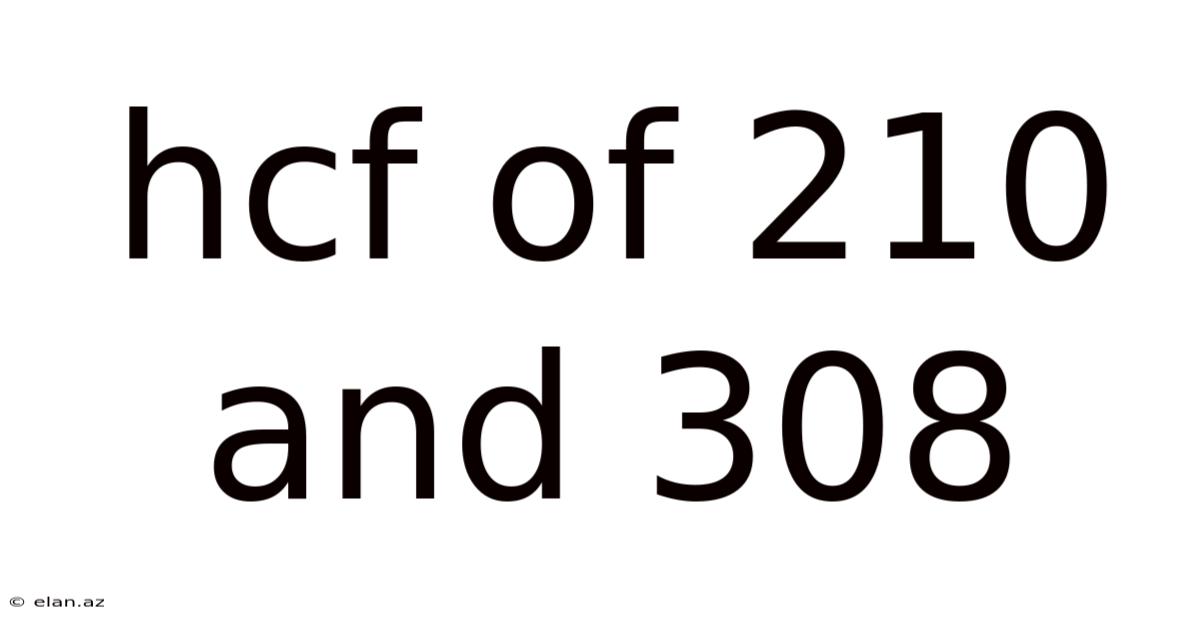
Table of Contents
Finding the Highest Common Factor (HCF) of 210 and 308: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will delve into the process of determining the HCF of 210 and 308, exploring various methods and providing a deeper understanding of the underlying principles. We'll cover multiple approaches, from prime factorization to the Euclidean algorithm, ensuring a comprehensive understanding for learners of all levels. This will also include frequently asked questions and solidify your understanding of this important mathematical concept.
Introduction to HCF and its Significance
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. Understanding HCF is crucial in various mathematical applications, including simplifying fractions, solving problems related to measurement and division, and forming a foundation for more advanced algebraic concepts. The ability to efficiently calculate the HCF is a valuable skill in both academic and practical contexts.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. The HCF is then determined by identifying the common prime factors and multiplying them together.
Let's apply this method to find the HCF of 210 and 308:
1. Prime Factorization of 210:
- We start by dividing 210 by the smallest prime number, 2: 210 ÷ 2 = 105
- 105 is not divisible by 2, so we move to the next prime number, 3: 105 ÷ 3 = 35
- 35 is divisible by 5: 35 ÷ 5 = 7
- 7 is a prime number.
Therefore, the prime factorization of 210 is 2 x 3 x 5 x 7.
2. Prime Factorization of 308:
- 308 is divisible by 2: 308 ÷ 2 = 154
- 154 is divisible by 2: 154 ÷ 2 = 77
- 77 is divisible by 7: 77 ÷ 7 = 11
- 11 is a prime number.
Therefore, the prime factorization of 308 is 2 x 2 x 7 x 11, or 2² x 7 x 11.
3. Identifying Common Factors:
Comparing the prime factorizations of 210 (2 x 3 x 5 x 7) and 308 (2² x 7 x 11), we identify the common prime factors: 2 and 7.
4. Calculating the HCF:
Multiply the common prime factors together: 2 x 7 = 14
Therefore, the HCF of 210 and 308 is 14.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF of two numbers, especially when dealing with larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the HCF.
Let's apply the Euclidean algorithm to find the HCF of 210 and 308:
1. Divide the larger number (308) by the smaller number (210):
308 ÷ 210 = 1 with a remainder of 98.
2. Replace the larger number with the smaller number (210) and the smaller number with the remainder (98):
210 ÷ 98 = 2 with a remainder of 14.
3. Repeat the process:
98 ÷ 14 = 7 with a remainder of 0.
Since the remainder is now 0, the last non-zero remainder (14) is the HCF.
Therefore, the HCF of 210 and 308 is 14.
Understanding the Mathematics Behind the Methods
Both methods, prime factorization and the Euclidean algorithm, are based on fundamental principles of number theory. The prime factorization method relies on the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. The Euclidean algorithm utilizes the property that the HCF of two numbers remains unchanged if the larger number is replaced by its difference with the smaller number. This iterative process efficiently leads to the HCF.
Illustrative Examples and Applications
Let's consider some real-world applications to solidify our understanding:
-
Simplifying Fractions: If you need to simplify the fraction 210/308, finding the HCF (14) allows you to reduce the fraction to its simplest form: 210/308 = 15/22.
-
Dividing Objects Equally: Imagine you have 210 red marbles and 308 blue marbles. You want to divide them into identical bags, each containing the same number of red and blue marbles. The HCF (14) tells you that you can create 14 bags, each containing 15 red marbles and 22 blue marbles.
-
Geometric Problems: Finding the largest square tile that can perfectly cover a rectangular floor with dimensions 210 cm and 308 cm involves calculating the HCF of 210 and 308. The HCF (14) signifies that the largest square tile would have a side length of 14 cm.
Frequently Asked Questions (FAQ)
Q1: What if the HCF of two numbers is 1?
A1: If the HCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
Q2: Can the Euclidean algorithm be used for more than two numbers?
A2: Yes, the Euclidean algorithm can be extended to find the HCF of more than two numbers. You would find the HCF of the first two numbers, then find the HCF of that result and the next number, and so on.
Q3: Which method is better, prime factorization or the Euclidean algorithm?
A3: For smaller numbers, prime factorization can be relatively straightforward. However, for larger numbers, the Euclidean algorithm is generally more efficient and less prone to errors.
Q4: Is there a way to visually represent the HCF?
A4: While there isn't a single universally accepted visual representation, Venn diagrams can be useful in understanding the concept. Each circle could represent the prime factors of a number, with the overlapping area showing the common factors. The product of the factors in the overlapping area represents the HCF.
Q5: Are there any online calculators or tools to find HCF?
A5: Yes, many websites and online calculators are available that can automatically calculate the HCF of two or more numbers. These can be helpful for verification or when dealing with very large numbers.
Conclusion
Finding the Highest Common Factor (HCF) is a fundamental skill in mathematics with applications across various fields. This article has explored two effective methods – prime factorization and the Euclidean algorithm – for calculating the HCF, focusing on the example of 210 and 308. Understanding these methods and their underlying principles provides a solid foundation for tackling more advanced mathematical concepts. Remember to practice regularly to hone your skills and become proficient in determining the HCF of any given numbers. The ability to efficiently find the HCF is not just a mathematical skill; it's a valuable tool for problem-solving in numerous contexts.
Latest Posts
Latest Posts
-
5 Letter Words Ending Ed
Sep 14, 2025
-
Hard Wearing Fabric Crossword Clue
Sep 14, 2025
-
How Do You Measure Light
Sep 14, 2025
-
Types Of Graphs Gcse Maths
Sep 14, 2025
-
5 Letter Word Ending K
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 210 And 308 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.