Hcf Of 210 And 693
elan
Sep 12, 2025 · 6 min read
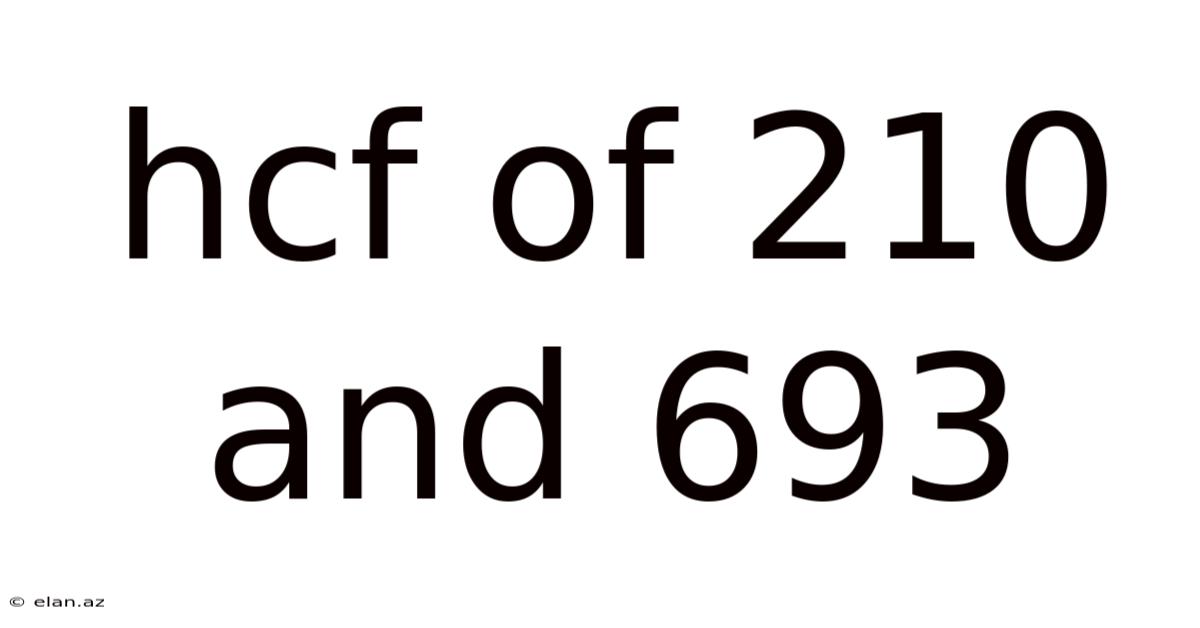
Table of Contents
Finding the Highest Common Factor (HCF) of 210 and 693: A Comprehensive Guide
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will comprehensively explore how to find the HCF of 210 and 693, employing various methods, explaining the underlying principles, and providing insights into the broader applications of this concept. Understanding HCF is crucial for simplifying fractions, solving algebraic problems, and even understanding more advanced mathematical concepts. We'll delve into different techniques, ensuring you grasp the core principles and can confidently apply them to other number pairs.
Introduction: What is the Highest Common Factor (HCF)?
The highest common factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that is a factor of both numbers. For example, the HCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. Finding the HCF is essential in various mathematical operations, from simplifying fractions to solving equations. In this article, we'll focus on finding the HCF of 210 and 693, exploring multiple methods to achieve this.
Method 1: Prime Factorization Method
This is a classic and reliable method for finding the HCF. It involves breaking down each number into its prime factors and then identifying the common factors. Prime factors are numbers divisible only by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Step 1: Find the prime factorization of 210.
210 can be broken down as follows:
210 = 2 × 105 = 2 × 3 × 35 = 2 × 3 × 5 × 7
Therefore, the prime factorization of 210 is 2 × 3 × 5 × 7.
Step 2: Find the prime factorization of 693.
693 can be broken down as follows:
693 = 3 × 231 = 3 × 3 × 77 = 3 × 3 × 7 × 11 = 3² × 7 × 11
Therefore, the prime factorization of 693 is 3² × 7 × 11.
Step 3: Identify common prime factors.
Now, compare the prime factorizations of 210 and 693:
210 = 2 × 3 × 5 × 7 693 = 3² × 7 × 11
The common prime factors are 3 and 7.
Step 4: Calculate the HCF.
To find the HCF, multiply the common prime factors together:
HCF(210, 693) = 3 × 7 = 21
Therefore, the highest common factor of 210 and 693 is 21.
Method 2: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF, particularly for larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Step 1: Divide the larger number by the smaller number.
Divide 693 by 210:
693 ÷ 210 = 3 with a remainder of 63.
Step 2: Replace the larger number with the remainder.
Now we have the numbers 210 and 63.
Step 3: Repeat the process.
Divide 210 by 63:
210 ÷ 63 = 3 with a remainder of 21.
Step 4: Continue until the remainder is 0.
Now we have the numbers 63 and 21.
Divide 63 by 21:
63 ÷ 21 = 3 with a remainder of 0.
Step 5: The HCF is the last non-zero remainder.
Since the remainder is 0, the last non-zero remainder (21) is the HCF.
Therefore, the highest common factor of 210 and 693 is 21.
Method 3: Listing Factors Method
This method is suitable for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Step 1: List the factors of 210.
Factors of 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210
Step 2: List the factors of 693.
Factors of 693: 1, 3, 7, 9, 11, 21, 33, 63, 77, 99, 231, 693
Step 3: Identify common factors.
The common factors of 210 and 693 are: 1, 3, 7, 21
Step 4: Determine the highest common factor.
The largest common factor is 21.
Therefore, the highest common factor of 210 and 693 is 21.
A Deeper Dive: Understanding the Significance of HCF
The HCF is more than just a mathematical concept; it has significant applications in various fields:
-
Simplifying Fractions: The HCF is crucial for simplifying fractions to their lowest terms. By dividing both the numerator and the denominator by their HCF, you obtain the simplest form of the fraction.
-
Algebraic Expressions: Finding the HCF helps in factoring algebraic expressions, simplifying them, and solving equations.
-
Number Theory: HCF plays a vital role in number theory, particularly in modular arithmetic and cryptography.
-
Real-World Applications: HCF finds applications in areas like dividing objects into equal groups, arranging items in arrays, and solving problems related to ratios and proportions. For example, if you need to divide 210 apples and 693 oranges into equally sized bags without any fruit left over, the HCF (21) determines the maximum number of bags you can make.
Frequently Asked Questions (FAQ)
-
Q: What if the HCF of two numbers is 1?
- A: If the HCF of two numbers is 1, they are called relatively prime or coprime. This means they have no common factors other than 1.
-
Q: Can the HCF of two numbers be larger than the smaller number?
- A: No, the HCF can never be larger than the smaller of the two numbers.
-
Q: Is there a limit to the number of methods to find the HCF?
- A: While the methods discussed here are the most common and efficient, there might be other approaches depending on the context and the tools available.
-
Q: How does the HCF relate to the Least Common Multiple (LCM)?
- A: The HCF and LCM of two numbers are related by the following formula: HCF(a, b) × LCM(a, b) = a × b. This relationship is useful for finding the LCM if you already know the HCF, and vice-versa.
Conclusion
Finding the HCF of 210 and 693, as demonstrated through prime factorization, the Euclidean algorithm, and the listing factors method, consistently yields the result of 21. Understanding the different approaches not only helps you solve specific problems but also provides a deeper appreciation for the fundamental concepts of number theory and their applications across various mathematical domains. Mastering the calculation of HCF is essential for building a solid foundation in mathematics and confidently tackling more complex problems. Remember to choose the method that best suits the numbers you are working with; for smaller numbers, the listing method might be quicker, while for larger numbers, the Euclidean algorithm offers efficiency and accuracy. The prime factorization method offers a strong conceptual understanding of the underlying principles. Through understanding these concepts and methods, you'll be well-equipped to approach similar problems with confidence and efficiency.
Latest Posts
Latest Posts
-
Assumptions Kinetic Theory Of Gases
Sep 12, 2025
-
Sq Mtr To Sq Yard
Sep 12, 2025
-
Games That Start With K
Sep 12, 2025
-
Exceptional Early Development Crossword Clue
Sep 12, 2025
-
Items That Start With V
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 210 And 693 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.