Hcf Of 22 And 27
elan
Sep 14, 2025 · 7 min read
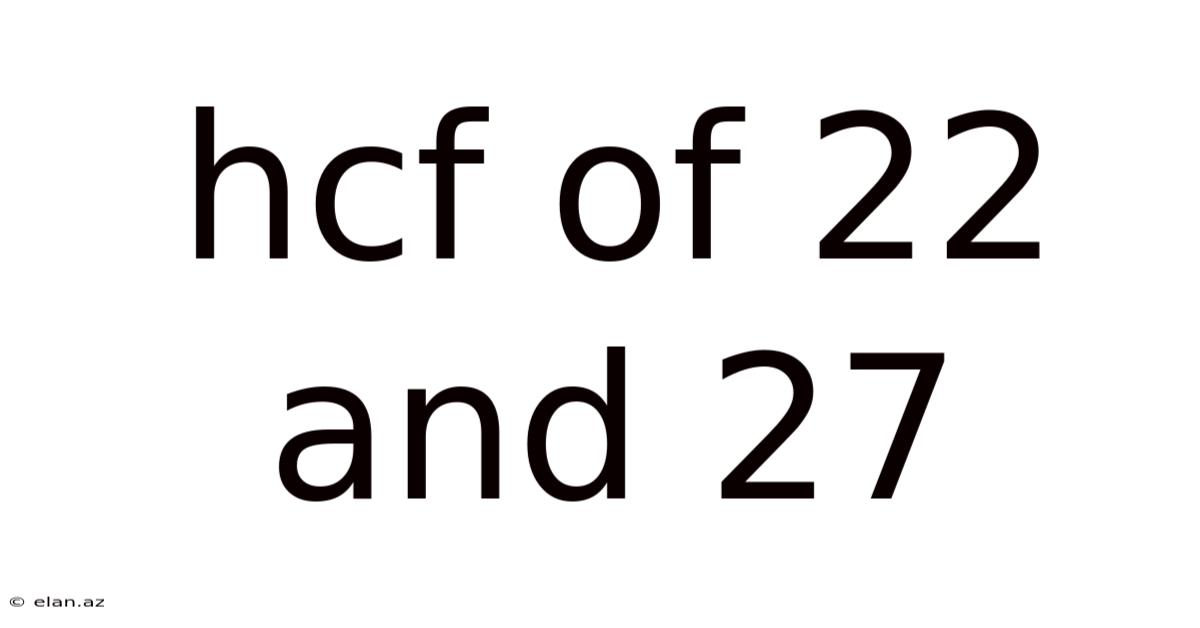
Table of Contents
Unveiling the Mysteries of HCF: A Deep Dive into Finding the Highest Common Factor of 22 and 27
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers might seem like a simple arithmetic task. But understanding the underlying principles and exploring different methods for calculation unveils a fascinating journey into the world of number theory. This article will delve deep into the process of finding the HCF of 22 and 27, exploring various techniques, explaining the underlying mathematical concepts, and answering frequently asked questions. By the end, you'll not only know the HCF of 22 and 27 but also possess a robust understanding of how to find the HCF of any two numbers.
Understanding the Concept of HCF
Before we jump into calculating the HCF of 22 and 27, let's establish a firm understanding of what HCF actually means. The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. It's the biggest number that is a factor of all the given numbers. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The highest of these common factors is 6, so the HCF of 12 and 18 is 6.
This concept is crucial in various mathematical applications, from simplifying fractions to solving problems in algebra and geometry. Understanding HCF helps us simplify complex expressions and find solutions to seemingly intricate mathematical puzzles.
Method 1: Prime Factorization Method
This is a classic and widely used method for finding the HCF. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Let's apply this method to find the HCF of 22 and 27:
-
Prime factorization of 22: 22 can be written as 2 x 11. Both 2 and 11 are prime numbers.
-
Prime factorization of 27: 27 can be written as 3 x 3 x 3, or 3³. 3 is a prime number.
-
Identifying Common Factors: Looking at the prime factorizations of 22 (2 x 11) and 27 (3 x 3 x 3), we see that there are no common prime factors.
-
Determining the HCF: Since there are no common prime factors, the HCF of 22 and 27 is 1. This means that 1 is the largest number that divides both 22 and 27 without leaving a remainder.
Method 2: Listing Factors Method
Another approach, particularly useful for smaller numbers, is listing all the factors of each number and then identifying the highest common factor.
-
Factors of 22: 1, 2, 11, 22
-
Factors of 27: 1, 3, 9, 27
-
Common Factors: The only common factor between the two lists is 1.
-
HCF: Therefore, the HCF of 22 and 27 is 1.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the HCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until we reach a point where the remainder is 0. The last non-zero remainder is the HCF.
Let's apply the Euclidean Algorithm to 22 and 27:
-
Step 1: Divide the larger number (27) by the smaller number (22). 27 = 22 x 1 + 5 (The remainder is 5)
-
Step 2: Replace the larger number (27) with the smaller number (22) and the smaller number (22) with the remainder (5). Repeat the division. 22 = 5 x 4 + 2 (The remainder is 2)
-
Step 3: Repeat the process again. 5 = 2 x 2 + 1 (The remainder is 1)
-
Step 4: Repeat once more. 2 = 1 x 2 + 0 (The remainder is 0)
-
HCF: The last non-zero remainder is 1. Therefore, the HCF of 22 and 27 is 1.
Why is the HCF of 22 and 27 Equal to 1? A Deeper Look
The fact that the HCF of 22 and 27 is 1 has a special significance in number theory. Numbers that have an HCF of 1 are called coprime or relatively prime. This means they share no common factors other than 1. This property is essential in various mathematical areas, including cryptography and modular arithmetic.
The prime factorization method clearly illustrates this coprimality. 22 (2 x 11) and 27 (3³) have entirely different sets of prime factors, indicating they are coprime. Their only common divisor is 1.
Applications of HCF in Real-World Scenarios
While finding the HCF of 22 and 27 might seem abstract, the concept has practical applications in various fields:
-
Simplifying Fractions: Finding the HCF of the numerator and denominator allows us to simplify fractions to their lowest terms.
-
Measurement and Division: When dividing objects or quantities into equal parts, understanding HCF helps determine the largest possible equal size. For example, if you have 22 red marbles and 27 blue marbles, and you want to divide them into identical groups, the largest possible group size would be 1 (one red marble and one blue marble in each group).
-
Scheduling and Timing: HCF can help in finding the least common multiple (LCM) which is crucial for scheduling events or tasks that repeat at different intervals.
-
Geometry and Measurement: Finding the dimensions of the largest square tile that can perfectly cover a rectangular area involves using the HCF of the rectangle's dimensions.
Frequently Asked Questions (FAQ)
Q: What if I have more than two numbers? How do I find the HCF?
A: You can extend any of the methods discussed above to find the HCF of more than two numbers. For the prime factorization method, you find the prime factorization of each number and identify the common prime factors raised to the lowest power. For the Euclidean Algorithm, you can find the HCF of two numbers and then find the HCF of the result and the next number, and so on.
Q: Is there a quick way to determine if two numbers are coprime?
A: While the prime factorization method is definitive, a quick check can be done by seeing if the two numbers share any obvious common factors (other than 1). If you can't immediately identify a common factor larger than 1, they are likely coprime, but you would still need a formal method like prime factorization or the Euclidean Algorithm for absolute certainty.
Q: Why is the Euclidean Algorithm more efficient for larger numbers?
A: The Euclidean Algorithm avoids the potentially tedious task of finding the complete prime factorization of large numbers, which can be computationally expensive. Its iterative process converges relatively quickly to the HCF, making it a more efficient approach for large numbers.
Q: Can a computer program be used to find the HCF?
A: Yes, computer programs can easily calculate the HCF using any of the methods described above. Programming languages like Python have built-in functions or libraries to compute the HCF efficiently.
Conclusion: Mastering the HCF
Finding the HCF, while seemingly a simple arithmetic operation, opens the door to a deeper understanding of number theory and its applications. We've explored multiple methods – prime factorization, listing factors, and the Euclidean Algorithm – to determine that the HCF of 22 and 27 is 1, highlighting the coprime nature of these two numbers. This understanding extends far beyond simple calculations; it's a foundational concept crucial in various fields of mathematics and beyond. By mastering these techniques, you've equipped yourself with a valuable tool for problem-solving and a deeper appreciation for the elegant structure of numbers. Remember that practice is key, so try finding the HCF of different pairs of numbers to solidify your understanding.
Latest Posts
Latest Posts
-
28 50 As A Percentage
Sep 14, 2025
-
Staines And Laleham Cricket Club
Sep 14, 2025
-
Active Or Passive Voice Worksheet
Sep 14, 2025
-
Hydrochloric Acid Plus Sodium Hydroxide
Sep 14, 2025
-
Sensory Relay And Motor Neurons
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 22 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.