Hcf Of 315 And 693
elan
Sep 14, 2025 · 6 min read
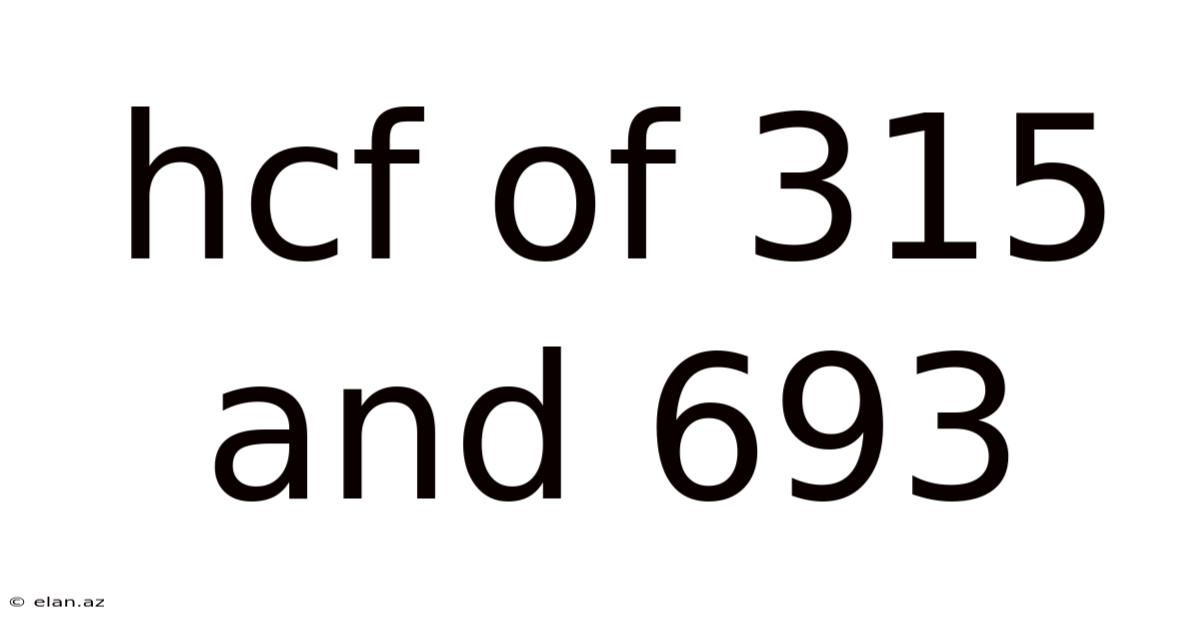
Table of Contents
Finding the Highest Common Factor (HCF) of 315 and 693: A Comprehensive Guide
Understanding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), is a fundamental concept in mathematics. This article provides a comprehensive exploration of how to find the HCF of 315 and 693, illustrating various methods and deepening your understanding of the underlying mathematical principles. We'll delve into different approaches, from prime factorization to the Euclidean algorithm, ensuring a thorough grasp of this crucial topic. This guide is perfect for students learning about number theory or anyone seeking a deeper understanding of HCF calculations.
Introduction: What is the Highest Common Factor (HCF)?
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. It's a crucial concept in simplifying fractions, solving algebraic equations, and understanding the relationships between numbers. In this article, we'll focus on finding the HCF of 315 and 693, employing several effective methods. Mastering these techniques will equip you to find the HCF of any pair of numbers efficiently.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Then, we identify the common prime factors and multiply them to find the HCF.
Step 1: Prime Factorization of 315
Let's start by finding the prime factors of 315:
- 315 is divisible by 3: 315 = 3 x 105
- 105 is divisible by 3: 105 = 3 x 35
- 35 is divisible by 5: 35 = 5 x 7
- 7 is a prime number.
Therefore, the prime factorization of 315 is 3 x 3 x 5 x 7, or 3² x 5 x 7.
Step 2: Prime Factorization of 693
Now, let's find the prime factors of 693:
- 693 is divisible by 3: 693 = 3 x 231
- 231 is divisible by 3: 231 = 3 x 77
- 77 is divisible by 7: 77 = 7 x 11
- 11 is a prime number.
Therefore, the prime factorization of 693 is 3 x 3 x 7 x 11, or 3² x 7 x 11.
Step 3: Identifying Common Factors
Comparing the prime factorizations of 315 (3² x 5 x 7) and 693 (3² x 7 x 11), we see that they share the common factors 3² and 7.
Step 4: Calculating the HCF
To find the HCF, we multiply the common prime factors: 3² x 7 = 9 x 7 = 63.
Therefore, the HCF of 315 and 693 is 63.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the HCF.
Step 1: Applying the Division Algorithm
We start by dividing the larger number (693) by the smaller number (315):
693 = 315 x 2 + 63
Step 2: Continuing the Process
Now, we divide the previous divisor (315) by the remainder (63):
315 = 63 x 5 + 0
Step 3: Identifying the HCF
Since the remainder is 0, the last non-zero remainder (63) is the HCF of 315 and 693.
Method 3: Listing Factors
While less efficient for larger numbers, listing factors can be a helpful method for smaller numbers like 315 and 693.
Step 1: Listing Factors of 315
The factors of 315 are: 1, 3, 5, 7, 9, 15, 21, 35, 45, 63, 105, 315.
Step 2: Listing Factors of 693
The factors of 693 are: 1, 3, 7, 9, 11, 21, 33, 63, 77, 99, 231, 693.
Step 3: Identifying the Highest Common Factor
By comparing the two lists, we find that the highest common factor is 63.
A Deeper Dive into the Mathematical Concepts
The HCF calculation is fundamentally tied to the concept of divisibility and prime factorization. Understanding prime numbers is crucial, as they are the building blocks of all other integers. Every number can be uniquely expressed as a product of prime numbers (Fundamental Theorem of Arithmetic). This uniqueness allows us to efficiently determine the common factors and, therefore, the HCF. The Euclidean algorithm, although seemingly simpler in its application, is deeply rooted in the properties of modular arithmetic and the division algorithm. It elegantly avoids the need for complete prime factorization, making it computationally more efficient for larger numbers.
Applications of HCF
The HCF finds practical applications in various mathematical and real-world scenarios:
-
Simplifying Fractions: The HCF is used to simplify fractions to their lowest terms. For example, the fraction 315/693 can be simplified to 5/11 by dividing both the numerator and denominator by their HCF, 63.
-
Solving Algebraic Equations: HCF plays a crucial role in solving certain types of algebraic equations, particularly those involving polynomial expressions.
-
Geometry and Measurement: The HCF is used in problems related to finding the largest possible square tiles that can be used to cover a rectangular floor without any gaps or overlaps.
-
Number Theory: HCF is a fundamental concept in number theory, forming the basis for many advanced theorems and algorithms.
Frequently Asked Questions (FAQ)
Q: What if the HCF of two numbers is 1?
A: If the HCF of two numbers is 1, they are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the HCF of two numbers be larger than either of the numbers?
A: No, the HCF can never be larger than the smaller of the two numbers. The HCF is, by definition, a divisor of both numbers.
Q: Are there other methods to find the HCF besides the ones discussed?
A: Yes, there are other, more advanced methods, particularly for finding the HCF of more than two numbers simultaneously. These often involve techniques from abstract algebra.
Q: Why is the Euclidean Algorithm more efficient for larger numbers?
A: The Euclidean Algorithm avoids the computationally expensive process of full prime factorization. It directly operates on the numbers themselves using the division algorithm, converging to the HCF much faster, especially when dealing with large numbers that have many prime factors.
Conclusion
Finding the Highest Common Factor (HCF) is a valuable skill in mathematics. We have explored three distinct methods – prime factorization, the Euclidean algorithm, and listing factors – each with its own strengths and weaknesses. Understanding these methods, and the underlying mathematical principles, allows you to tackle HCF problems efficiently and confidently. Remember, choosing the most appropriate method depends on the size of the numbers involved and your comfort level with different approaches. The Euclidean algorithm is generally preferred for larger numbers due to its computational efficiency. Regardless of the method employed, the ultimate goal remains the same: identifying the largest number that perfectly divides both numbers in question. This foundational concept continues to be vital throughout various branches of mathematics and its applications.
Latest Posts
Latest Posts
-
How Large Is 5 Acres
Sep 14, 2025
-
Iron Density In Kg M3
Sep 14, 2025
-
Hcf Of 54 And 120
Sep 14, 2025
-
Encouraging Words Starting With E
Sep 14, 2025
-
16 25 As A Percentage
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 315 And 693 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.